總結Python常用的魔法方法
一、算數運算符的魔法方法
- python2.2以後,對類和類型進行瞭統一,做法就是講int()、float()、str()、list()、tuple()這些BIF轉換為工廠函數(類對象)
- 給出以下算數運算符對應的魔法方法,前面和後面都被雙下劃線包尾說明是魔法方法
| 運算符 | 對應的魔法方法 | 中文註釋 |
| + | __ add__(self, other) | 加法 |
| – | __ sub__(self, other) | 減法 |
| * | __ mul__(self, other) | 乘法 |
| / | __ truediv__(self, other) | 真除法 |
| // | __ floordiv__(self, other) | 整數除法 |
| % | __ mod__(self, other) | 取餘除法 |
| divmod(a, b) | __ divmod__(self, other) | 把除數和餘數運算結果結合,divmod(a,b)返回值是一個元組(a//b, a%b) |
| ** | __ pow__(self, other[,modulo]) | self的other次方再對modulo取餘 |
| << | __ lshift__(self, other) | 按位左移 |
| >> | __ rshift__(self, other) | 按位右移 |
| & | __ and__(self, other) | 按位與操作 |
| ^ | __ xor__(self, other) | 按位異或操作(同為0,異為1) |
| 丨 | __ or__(self, other) | 按位或操作(有1則1) |
| – | – | – |
- eg:
>>> type(len)
<class 'builtin_function_or_method'> #普通的BIF
>>> type(int)
<class 'type'> #工廠函數(類對象),當調用它們的時候,其實就是創建瞭一個相應的實例對象
>>> type(dir)
<class 'builtin_function_or_method'>
>>> type(list)
<class 'type'>
>>> a = int('123') #創建一個相應的實例對象a
>>> b = int('345')
>>> a + b #python在兩個對象進行相加操作
468
- eg:舉個例子,下面定義一個比較特立獨行的類:
繼承int,並重寫__add__方法
>>> class New_int(int):
def __add__(self,other):
return int.__sub__(self,other)
def __sub__(self,other):
return int.__add__(self,other)
>>> a = New_int(3)
>>> b = New_int(5)
>>> a + b #兩個對象相加,觸發 __add__(self,other)方法
-2
>>> a - b
8
>>>
實例2:錯誤寫法,會造成無限遞歸
>>> class New_int(int):
def __add__(self,other):
return (self + other)
def __sub__(self,other):
return (self - other)
>>> class New_int(int):
def __add__(self,other):
return (int(self) + int(other)) #將self與other強制轉換為整型,所以不會出現兩個對象相加觸發__add__()方法
def __sub__(self,other):
return (int(self) - int(other))
>>> a = New_int(3)
>>> b = New_int(5)
>>> a + b
8
二、反運算相關的魔法方法
- 反運算相關的魔法方法
| 魔法方法 | 定義 |
| __ radd__(self, other) | 定義加法的行為:+(當左操作數不支持相應的操作時被調用) |
| __ rsub__(self, other) | 定義減法的行為:-(當左操作數不支持相應的操作時被調用) |
| __ rmul__(self, other) | 定義乘法的行為:*(當左操作數不支持相應的操作時被調用) |
| __ rtruediv__(self, other) | 定義真除法的行為:/(當左操作數不支持相應的操作時被調用) |
| __ rfloordiv__(self, other) | 定義整數除法的行為://(當左操作數不支持相應的操作時被調用) |
| __ rmod__(self, other) | 定義取模算法的行為:%(當左操作數不支持相應的操作時被調用) |
| __ rdivmod__(self, other) | 定義當被divmod()調用時的行為(當左操作數不支持相應的操作時被調用) |
| __ rpow__(self, other) | 定義當被power()調用或**運算時的行為(當左操作數不支持相應的操作時被調用) |
| __ rlshift__(self, other) | 定義按位左移位的行為:<<(當左操作數不支持相應的操作時被調用) |
| __ rrshift__(self, other) | 定義按位右移位的行為:>>(當左操作數不支持相應的操作時被調用) |
| __ rand__(self, other) | 定義按位與操作的行為:&(當左操作數不支持相應的操作時被調用) |
| __ rxor__(self, other) | 定義按位異或操作的行為:^(當左操作數不支持相應的操作時被調用) |
| __ ror__(self, other) | 定義按位或操作的行為:丨(當左操作數不支持相應的操作時被調用) |
| – | – |
>>> class int(int):
def __add__(self,other):
return int.__sub__(self,other)
>>> a = int(3)
>>> b = int(2)
>>> a + b
1
反運算與算術運算符的不同之處是,反運算多瞭一個'r',例如 __add__()的反運算對應為 __radd__()
>>> a + b
這裡a是加數,b是被加數,如果a對象的__add__()方法沒有實現或者不支持相應的操作,那麼python就會自動調用b的__radd__()方法
實例:
>>> class Nint(int):
def __radd__(self,other):
return int.__sub__(self,other)
>>> a = Nint(5)
>>> b = Nint(3)
>>> a + b #由於a對象默認有__add__()方法,所以b的__radd__()沒有執行
8
實例2:
>>> class Nint(int):
def __radd__(self,other):
return int.__sub__(self,other)
>>> b = Nint(5)
>>> 3 + b #由於3無__add__()方法,所以執行b的反運算__radd__(self,other)方法,其中self是b對象
2
eg:註:在重寫反運算魔法方法時,一定要註意順序問題。得到的應該是個負數,所以順序改變下。
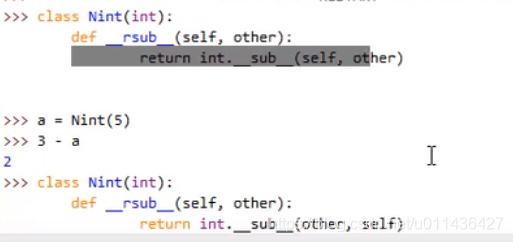
三、增量賦值運算
增量賦值運算的魔法方法
| 魔法方法 | 定義 |
| __ iadd__(self, other) | 定義賦值加法的行為:+= |
| __ isub__(self, other) | 定義賦值減法的行為:-= |
| __ imul__(self, other) | 定義賦值乘法的行為:*= |
| __ itruediv__(self, other) | 定義賦值真除法的行為:/= |
| __ ifloordiv__(self, other) | 定義賦值整數除法的行為://= |
| __ imod__(self, other) | 定義賦值取模算法的行為:%= |
| __ ipow__(self, other) | 定義賦值冪運算的行為:**= |
| __ ilshift__(self, other) | 定義賦值按位左移位的行為:<<= |
| __ irshift__(self, other) | 定義賦值按位右移位的行為:>>= |
| __ iand__(self, other) | 定義賦值按位與操作的行為:&= |
| __ ixor__(self, other) | 定義賦值按位異或操作的行為:^= |
| __ ior__(self, other) | 定義賦值按位或操作的行為:丨= |
| – | – |
四、一元操作符
- 一元操作符的魔法方法
| 魔法方法 | 定義 |
| __ neg__(self) | 定義正號的行為:+x |
| __ pos__(self) | 定義負號的行為:-x |
| __ abs__(self) | 定義當被abs()調用時的行為 |
| __ invert__(self) | 定義按位求反的行為:~x |
| – | – |
到此這篇關於總結Python常用的魔法方法的文章就介紹到這瞭,更多相關Python魔法方法內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!