Java數據結構與算法入門實例詳解
第一部分:Java數據結構
要理解Java數據結構,必須能清楚何為數據結構?
數據結構:
- Data_Structure,它是儲存數據的一種結構體,在此結構中儲存一些數據,而這些數據之間有一定的關系。
- 而各數據元素之間的相互關系,又包括三個組成成分,數據的邏輯結構,數據的存儲結構和數據運算結構。
- 而一個數據結構的設計過程分成抽象層、數據結構層和實現層。
數據結構在Java的語言體系中按邏輯結構可以分為兩大類:線性數據結構和非線性數據結構。
一、Java數據結構之:線性數據結構
線性數據結構:常見的有一維數組,線性表,棧,隊列,雙隊列,串。
1:一維數組
在Java裡面常用的util有:String [],int [],ArrayList,Vector,CopyOnWriteArrayList等。及可以同過一維數組[]自己實現不同邏輯結構的Util類。而ArrayList封裝瞭一些[]的基本操作方法。ArrayList和Vector的區別是:Vector是線程安全的,方法同步。CopyOnWriteArrayList也是線程安全的但效率要比Vector高很多。(PS:如果不懂出門右拐看另一篇chat)。
數組這種數據結構典型的操作方法,是根據下標進行操作的,所以insert的的時候可以根據下標插入到具體的某個位置,但是這個時候它後面的元素都得往後面移動一位。所以插入效率比較低,更新,刪除效率也比較低,而查詢效率非常高,查詢效率時間復雜度是1。
2: 線性表
線性表是有序的儲存結構、鏈式的儲存結構。鏈表的物理儲存空間是不連續的,鏈表的每一個節點都知道上一個節點、或者下一個節點是誰,通常用Node表示。常見的有順序鏈表(LinkedList、Linked***),單項鏈表(裡面隻有Node類),雙向鏈表(兩個Node類),循環鏈表(多個Node類)等。
操作方法:插入效率比較高,插入的時候隻需要改變節點的前後節點的連接即可。而查詢效率就比較低瞭,如果實現的不好,需要整個鏈路找下去才能找到應該找的元素。所以常見的方法有:add(index,element),addFirst(element),addLast(element)。getFirst(),getLast(),get(element)等。
常見的Uitil有:LinkedList,LinkedMap等,而這兩個JDK底層也做瞭N多優化,可以有效避免查詢效率低的問題。當自己實現的時候需要註意。其實樹形結構可以說是非線性的鏈式儲存結構。
3: 棧Stack
棧,最主要的是要實現先進後出,後進先出的邏輯結構。來實現一些場景對邏輯順序的要求。所以常用的方法有push(element)壓棧,pop()出棧。
java.util.Stack。就實現瞭這用邏輯。而Java的Jvm裡面也用的到瞭此種數據結構,就是線程棧,來保證當前線程的執行順序。
4:隊列
隊列,隊列是一種特殊的線性數據結構,隊列隻能允許在隊頭,隊尾進行添加和查詢等相關操作。隊列又有單項有序隊列,雙向隊列,阻塞隊列等。
Queue這種數據結構註定瞭基本操作方法有:add(E e)加入隊列,remove(),poll()等方法。
隊列在Java語言環境中是使用頻率相當高的數據結構,所有其實現的類也很多來滿足不同場景。


使用場景也非常多,如線程池,mq,連接池等。
5:串
串:也稱字符串,是由N個字符組成的優先序列。在Java裡面就是指String,而String裡面是由chat[]來進行儲存。
KMP算法: 這個算法一定要牢記,Java數據結構這本書裡面針對字符串的查找匹配算法也隻介紹瞭一種。關鍵點就是:在字符串比對的時候,主串的比較位置不需要回退的問題。
二、Java數據結構之:非線性數據結構
非線性數據結構:常見的有:多維數組,集合,樹,圖,散列表(hash).
1:多維數組
一維數組前面咱也提到瞭,多維數組無非就是String [][],int[][]等。Java裡面很少提供這樣的工具類,而java裡面tree和圖底層的native方法用瞭多維數組來儲存。
2:集合
由一個或多個確定的元素所構成的整體叫做集合。在Java裡面可以去廣義的去理解為實現瞭Collection接口的類都叫集合。
3:樹
樹形結構,作者覺得它是一種特殊的鏈形數據結構。最少有一個根節點組成,可以有多個子節點。樹,顯然是由遞歸算法組成。
樹的特點:
在一個樹結構中,有且僅有一個結點沒有直接父節點,它就是根節點。除瞭根節點,其他結點有且隻有一個直接父節點每個結點可以有任意多個直接子節點。
樹的數據結構又分如下幾種:
1) 自由樹/普通樹:對子節點沒有任何約束。
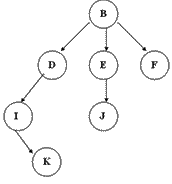
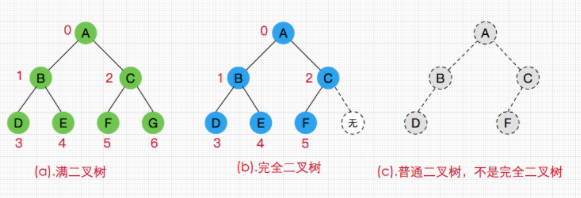
2) 二叉樹:每個節點最多含有兩個子節點的樹稱為二叉樹。
2.1) 一般二叉樹:每個子節點的父親節點不一定有兩個子節點的二叉樹成為一般二叉樹。
2.2) 完全二叉樹:對於一顆二叉樹,假設其深度為d(d>1)。除瞭第d層外,其它各層的節點數目均已達最大值,且第d層所有節點從左向右連續地緊密排列,這樣的二叉樹被稱為完全二叉樹;
2.3) 滿二叉樹:所有的節點都是二叉的二叉樹成為滿二叉樹。
3) 二叉搜索樹/BST:binary search tree,又稱二叉排序樹、二叉查找樹。是有序的。要點:如果不為空,那麼其左子樹節點的值都小於根節點的值;右子樹節點的值都大於根節點的值。
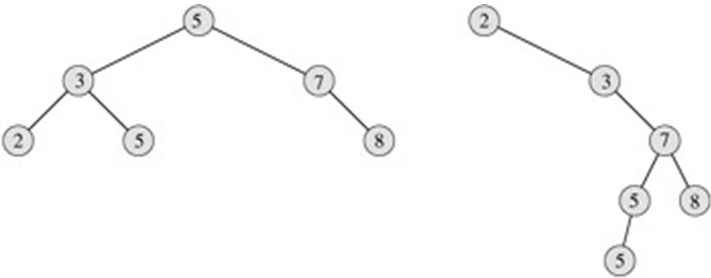
3.1) 二叉平衡樹:二叉搜索樹,是有序的排序樹,但左右兩邊包括子節點不一定平衡,而二叉平衡樹是排序樹的一種,並且加點條件,就是任意一個節點的兩個叉的深度差不多(比如差值的絕對值小於某個常數,或者一個不能比另一個深出去一倍之類的)。這樣的樹可以保證二分搜索任意元素都是O(log n)的,一般還附帶帶有插入或者刪除某個元素也是O(log n)的的性質。
為瞭實現,二叉平衡樹又延伸出來瞭一些算法,業界常見的有AVL、和紅黑算法,所以又有以下兩種樹:
3.1.1) AVL樹:最早的平衡二叉樹之一。應用相對其他數據結構比較少。windows對進程地址空間的管理用到瞭AVL樹。
3.1.2) 紅黑樹:通過制定瞭一些紅黑標記和左右旋轉規則來保證二叉樹平衡。
紅黑樹的5條性質:
每個結點要麼是紅的,要麼是黑的。根結點是黑的。每個葉結點(葉結點即指樹尾端NIL指針或NULL結點)是黑的。如果一個結點是紅的,那麼它的倆個兒子都是黑的。對於任一結點而言,其到葉結點樹尾端NIL指針的每一條路徑都包含相同數目的黑結點。
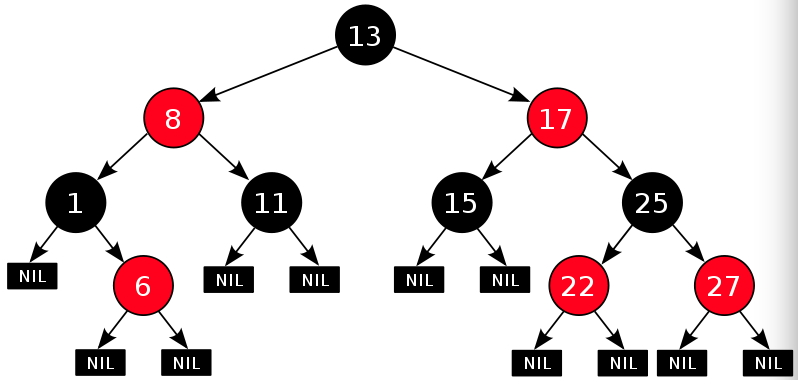
4) B-tree:又稱B樹、B-樹。又叫平衡(balance)多路查找樹。樹中每個結點最多含有m個孩子(m>=2)。它類似普通的平衡二叉樹,不同的一點是B-樹允許每個節點有更多的子節點。
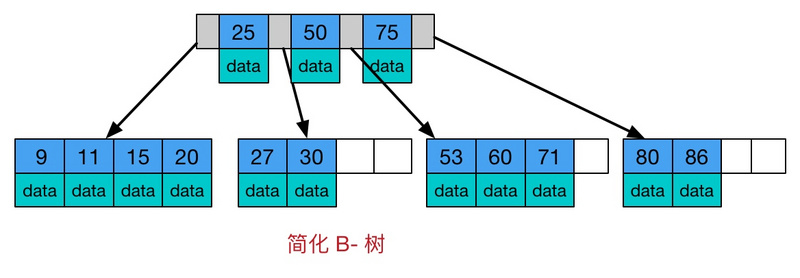
4) B+tree:又稱B+。是B-樹的變體,也是一種多路搜索樹。
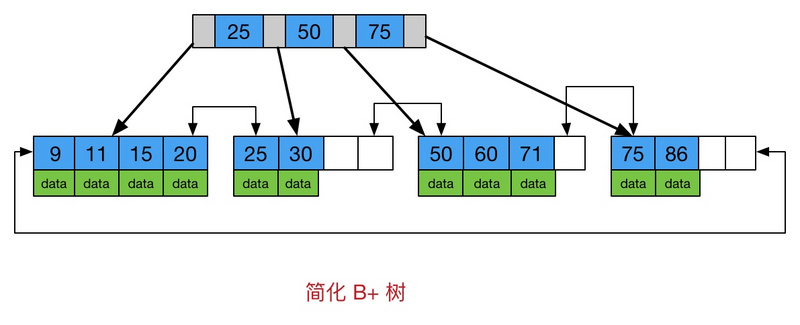
樹總結:
樹在Java裡面應用的也比較多。非排序樹,主要用來做數據儲存和展示。而排序樹,主要用來做算法和運算,HashMap裡面的TreeNode就用到瞭紅黑樹算法。而B+樹在數據庫的索引原理裡面有典型的應用。
4:Hash
Hash概念:
Hash,一般翻譯做“散列”,也有直接音譯為“哈希”的,就是把任意長度的輸入(又叫做預映射, pre-image),變換成固定長度的輸出,該輸出就是散列值。一般通過Hash算法實現。
所謂的Hash算法都是散列算法,把任意長度的輸入,變換成固定長度的輸出,該輸出就是散列值.(如:MD5,SHA1,加解密算法等)
簡單的說就是一種將任意長度的消息壓縮到某一固定長度的消息摘要的函數。
Java中的hashCode:
我們都知道所有的class都是Object的子類,既所有的class都會有默認Object.java裡面的hashCode的方法,如果自己沒有重寫,默認情況就是native方法通過對象的內存的+對象的值然後通過hash散列算法計算出來個int的數字。
最大的特性是:不同的對象,不同的值有可能計算出來的hashCode可能是一樣的。
Hash表:
Java中數據存儲方式最底層的兩種結構,一種是數組,另一種就是鏈表。而Hash表就是綜合瞭這兩種數據結構。
如:HashTable,HashMap。這個時候就得提一下HashMap的原理瞭,默認16個數組儲存,通過Hash值取模放到不同的桶裡面去。(註意:JDK1.8此處算法又做瞭改進,數組裡面的值會演變成樹形結構。)
哈希表具有較快(常量級)的查詢速度,及相對較快的增刪速度,所以很適合在海量數據的環境中使用。一般實現哈希表的方法采用“拉鏈法”,我們可以理解為“鏈表的數組”。
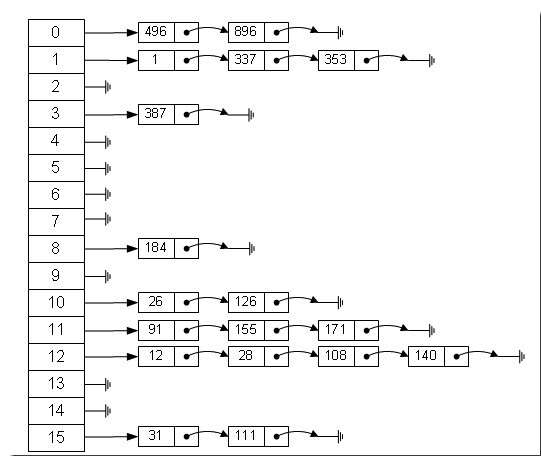
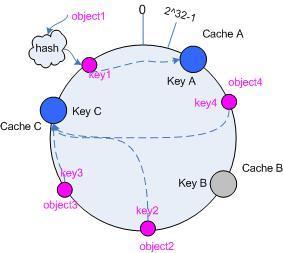
一致性Hash:
我們查看一下HashMap的原理,其實發現Hash很好的解決瞭單體應用情況下的數據查找和插入的速度問題。但是畢竟單體應用的儲存空間是有限的,所有在分佈式環境下,應運而生瞭一致性Hash算法。
用意和hashCode的用意一樣,隻不過它是取模放在不同的IP機器上而已。具體算法可以找一下相關資料。
而一致性Hash需要註意的就是默認分配的桶比較多些,而當其中一臺機器掛瞭,影響的面比較小一些。
需要註意的是,相同的內容算出來的hash一定是一樣的。既:冪等性。
第二部分:Java基本算法
理解瞭Java數據結構,還必須要掌握一些常見的基本算法。 理解算法之前必須要先理解的幾個算法的概念:
空間復雜度:一句來理解就是,此算法在規模為n的情況下額外消耗的儲存空間。
時間復雜度:一句來理解就是,此算法在規模為n的情況下,一個算法中的語句執行次數稱為語句頻度或時間頻度。
穩定性:主要是來描述算法,每次執行完,得到的結果都是一樣的,但是可以不同的順序輸入,可能消耗的時間復雜度和空間復雜度不一樣。
一、二分查找算法
二分查找又稱折半查找,優點是比較次數少,查找速度快,平均性能好,占用系統內存較少;其缺點是要求待查表為有序表,且插入刪除困難。這個是基礎,最簡單的查找算法瞭。
public static void main(String[] args) {
int srcArray[] = {3,5,11,17,21,23,28,30,32,50,64,78,81,95,101};
System.out.println(binSearch(srcArray, 28));
}
/**
* 二分查找普通循環實現
*
* @param srcArray 有序數組
* @param key 查找元素
* @return
*/
public static int binSearch(int srcArray[], int key) {
int mid = srcArray.length / 2;
// System.out.println("=:"+mid);
if (key == srcArray[mid]) {
return mid;
}
//二分核心邏輯
int start = 0;
int end = srcArray.length - 1;
while (start <= end) {
// System.out.println(start+"="+end);
mid = (end - start) / 2 + start;
if (key < srcArray[mid]) {
end = mid - 1;
} else if (key > srcArray[mid]) {
start = mid + 1;
} else {
return mid;
}
}
return -1;
}
二分查找算法如果沒有用到遞歸方法的話,隻會影響CPU。對內存模型來說影響不大。時間復雜度log2n,2的開方。空間復雜度是2。一定要牢記這個算法。應用的地方也是非常廣泛,平衡樹裡面大量采用。
二、遞歸算法
遞歸簡單理解就是方法自身調用自身。
public static void main(String[] args) {
int srcArray[] = {3,5,11,17,21,23,28,30,32,50,64,78,81,95,101};
System.out.println(binSearch(srcArray, 0,15,28));
}
/**
* 二分查找遞歸實現
*
* @param srcArray 有序數組
* @param start 數組低地址下標
* @param end 數組高地址下標
* @param key 查找元素
* @return 查找元素不存在返回-1
*/
public static int binSearch(int srcArray[], int start, int end, int key) {
int mid = (end - start) / 2 + start;
if (srcArray[mid] == key) {
return mid;
}
if (start >= end) {
return -1;
} else if (key > srcArray[mid]) {
return binSearch(srcArray, mid + 1, end, key);
} else if (key < srcArray[mid]) {
return binSearch(srcArray, start, mid - 1, key);
}
return -1;
}
遞歸幾乎會經常用到,需要註意的一點是:遞歸不光影響的CPU。JVM裡面的線程棧空間也會變大。所以當遞歸的調用鏈長的時候需要-Xss設置線程棧的大小。
三、八大排序算法
一、直接插入排序(Insertion Sort)
二、希爾排序(Shell Sort)
三、選擇排序(Selection Sort)
四、堆排序(Heap Sort)
五、冒泡排序(Bubble Sort)
六、快速排序(Quick Sort)
七、歸並排序(Merging Sort)
八、基數排序(Radix Sort)
八大算法,網上的資料就比較多瞭。
吐血推薦參考資料:git hub 八大排序算法詳解。此大神比作者講解的還詳細,作者就不在這裡,描述重復的東西瞭,作者帶領大傢把重點的兩個強調一下,此兩個是必須要掌握的。
1:冒泡排序
基本思想:
冒泡排序(Bubble Sort)是一種簡單的排序算法。它重復地走訪過要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。走訪數列的工作是重復地進行直到沒有再需要交換,也就是說該數列已經排序完成。這個算法的名字由來是因為越小的元素會經由交換慢慢“浮”到數列的頂端。
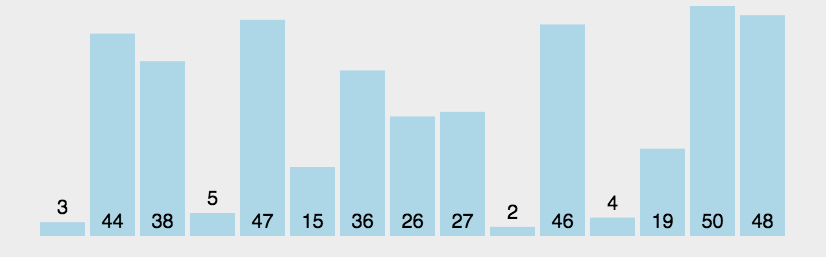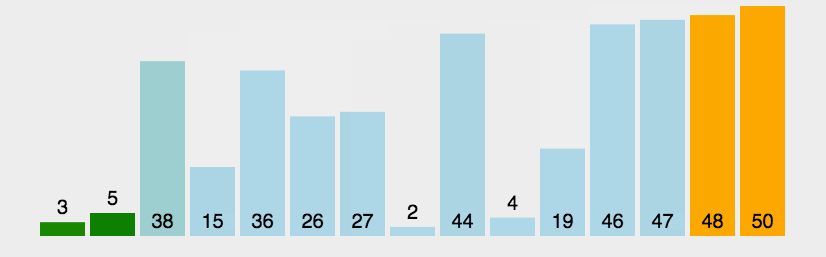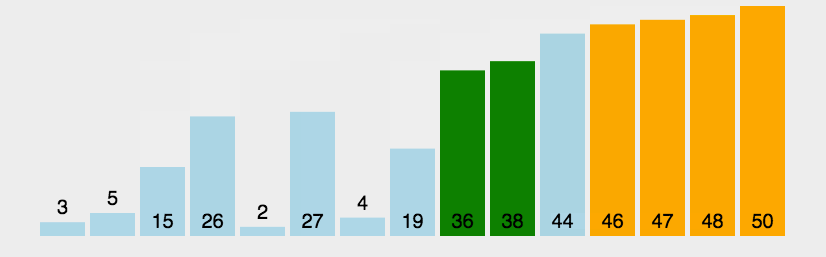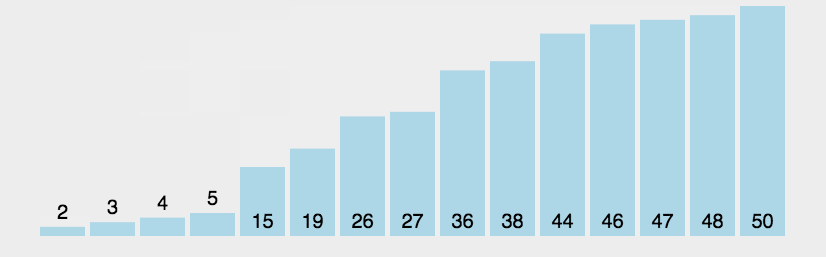
以下是冒泡排序算法復雜度:
| 平均時間復雜度 | 最好情況 | 最壞情況 | 空間復雜度 |
|---|---|---|---|
| O(n²) | O(n) | O(n²) | O(1) |
冒泡排序是最容易實現的排序, 最壞的情況是每次都需要交換, 共需遍歷並交換將近n²/2次, 時間復雜度為O(n²). 最佳的情況是內循環遍歷一次後發現排序是對的, 因此退出循環, 時間復雜度為O(n). 平均來講, 時間復雜度為O(n²). 由於冒泡排序中隻有緩存的temp變量需要內存空間, 因此空間復雜度為常量O(1).
Tips: 由於冒泡排序隻在相鄰元素大小不符合要求時才調換他們的位置, 它並不改變相同元素之間的相對順序, 因此它是穩定的排序算法.
/**
* 冒泡排序
*
* ①. 比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。
* ②. 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。這步做完後,最後的元素會是最大的數。
* ③. 針對所有的元素重復以上的步驟,除瞭最後一個。
* ④. 持續每次對越來越少的元素重復上面的步驟①~③,直到沒有任何一對數字需要比較。
* @param arr 待排序數組
*/
public static void bubbleSort(int[] arr){
for (int i = arr.length; i > 0; i--) { //外層循環移動遊標
for(int j = 0; j < i && (j+1) < i; j++){ //內層循環遍歷遊標及之後(或之前)的元素
if(arr[j] > arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
System.out.println("Sorting: " + Arrays.toString(arr));
}
}
}
}
2:快速排序
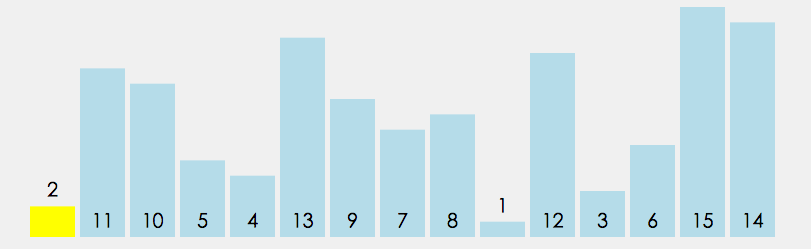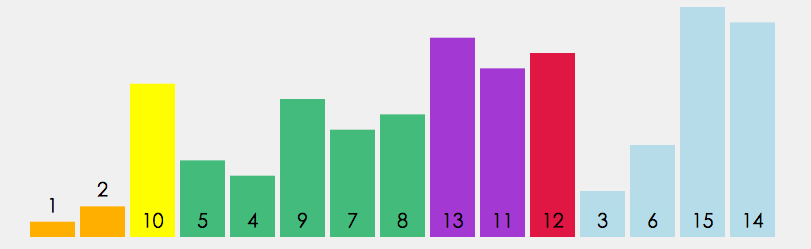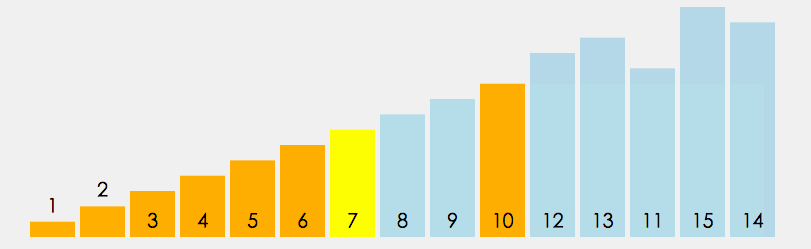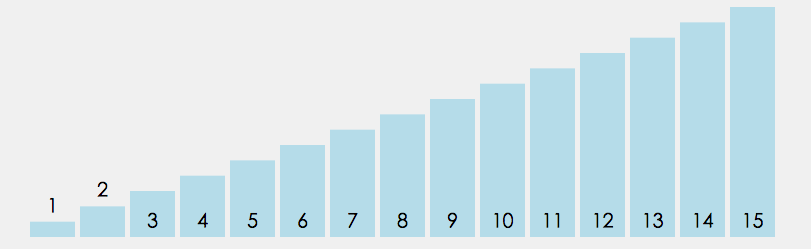
快速排序使用分治策略來把一個序列(list)分為兩個子序列(sub-lists)。步驟為:
①. 從數列中挑出一個元素,稱為”基準”(pivot)。
②. 重新排序數列,所有比基準值小的元素擺放在基準前面,所有比基準值大的元素擺在基準後面(相同的數可以到任一邊)。在這個分區結束之後,該基準就處於數列的中間位置。這個稱為分區(partition)操作。
③. 遞歸地(recursively)把小於基準值元素的子數列和大於基準值元素的子數列排序。
遞歸到最底部時,數列的大小是零或一,也就是已經排序好瞭。這個算法一定會結束,因為在每次的迭代(iteration)中,它至少會把一個元素擺到它最後的位置去。
代碼實現:
用偽代碼描述如下:
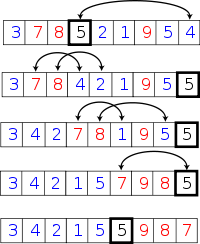
①. i = L; j = R; 將基準數挖出形成第一個坑a[i]。
②.j–,由後向前找比它小的數,找到後挖出此數填前一個坑a[i]中。
③.i++,由前向後找比它大的數,找到後也挖出此數填到前一個坑a[j]中。
④.再重復執行②,③二步,直到i==j,將基準數填入a[i]中。
快速排序采用“分而治之、各個擊破”的觀念,此為原地(In-place)分區版本。
/**
* 快速排序(遞歸)
*
* ①. 從數列中挑出一個元素,稱為"基準"(pivot)。
* ②. 重新排序數列,所有比基準值小的元素擺放在基準前面,所有比基準值大的元素擺在基準後面(相同的數可以到任一邊)。在這個分區結束之後,該基準就處於數列的中間位置。這個稱為分區(partition)操作。
* ③. 遞歸地(recursively)把小於基準值元素的子數列和大於基準值元素的子數列排序。
* @param arr 待排序數組
* @param low 左邊界
* @param high 右邊界
*/
public static void quickSort(int[] arr, int low, int high){
if(arr.length <= 0) return;
if(low >= high) return;
int left = low;
int right = high;
int temp = arr[left]; //挖坑1:保存基準的值
while (left < right){
while(left < right && arr[right] >= temp){ //坑2:從後向前找到比基準小的元素,插入到基準位置坑1中
right--;
}
arr[left] = arr[right];
while(left < right && arr[left] <= temp){ //坑3:從前往後找到比基準大的元素,放到剛才挖的坑2中
left++;
}
arr[right] = arr[left];
}
arr[left] = temp; //基準值填補到坑3中,準備分治遞歸快排
System.out.println("Sorting: " + Arrays.toString(arr));
quickSort(arr, low, left-1);
quickSort(arr, left+1, high);
}
以下是快速排序算法復雜度:
| 平均時間復雜度 | 最好情況 | 最壞情況 | 空間復雜度 |
|---|---|---|---|
| O(nlog₂n) | O(nlog₂n) | O(n²) | O(1)(原地分區遞歸版) |
快速排序排序效率非常高。 雖然它運行最糟糕時將達到O(n²)的時間復雜度, 但通常平均來看, 它的時間復雜為O(nlogn), 比同樣為O(nlogn)時間復雜度的歸並排序還要快. 快速排序似乎更偏愛亂序的數列, 越是亂序的數列, 它相比其他排序而言, 相對效率更高.