關於二分法查找Java的實現及解析
二分法查找
概述
二分查找也稱折半查找(Binary Search),它是一種效率較高的查找方法。
但是,折半查找要求線性表必須采用順序存儲結構,而且表中元素按關鍵字有序排列。
歸並排序即運用瞭二分法的思想。首先需要一個由小到大排序好的數組,先對比中間的值,如果比要找的大,則向前找,取中間值前面的一半再找中間值再對比。
如果比要找的小,則向後找,取中間值後面的一半再取中間值再對比。
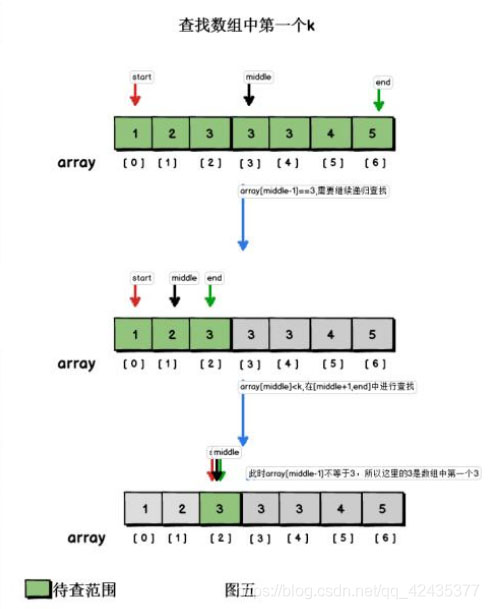
遞歸實現
這裡,我使用瞭遞歸的方法進行實現。
首先需要確認查找的范圍,即有一個左索引和右索引,每次取(left+right)/2為中間值,比較要查找的元素和中間值的大小,若中間值大,則向前找,即遞歸范圍為left ,mid-1。反之向右找,即遞歸范圍mid+1,right。若相等即為找到。
但是需要繼續向此索引的前後找找看有沒有和其相等的值,一並加入到集合中,最後返回這個集合。
遞歸實現代碼
package search;
import java.util.ArrayList;
import java.util.List;
public class BinarySearch {
public static void main(String[] args) {
int[] array = {1,1,1,2,3,4,5,6,7};
List<Integer> integers = binarySearch(array, 0, array.length - 1, 1);
// for (Integer integer : integers) {
// System.out.print(integer+ " ");
// }
System.out.println(integers);
}
public static List<Integer> binarySearch(int[] array, int left, int right, int value){
//如果左索引大於右索引,則說明全部遍歷完瞭,也沒有找到相應的值,返回空集合即可
if (left>right){
return new ArrayList<Integer>();
}
//獲取中間值的下標(二分)
int mid = (left+right)/2;
//如果要找的值比中間值小,則繼續向左找
if (value < array[mid]){
return binarySearch(array, left, mid-1, value);
//要找的值比中間值小大,則向右找
}else if (value > array[mid]){
return binarySearch(array, mid+1, right, value);
//否則,說明相等,找到瞭
}else {
//找到一個,還需要向左右找找看有沒有相同的值
List<Integer> resultList = new ArrayList();
//向左循環找,如果有,則加入到集合中
int temp = mid - 1;
while (temp>=0 && array[temp] == value){
resultList.add(temp);
temp -= 1;
}
//向右循環找,如果有,則加入到集合中
temp = mid + 1;
while (temp < array.length && array[temp] == value){
resultList.add(temp);
temp += 1;
}
//將一開始找到的那個索引頁加入到集合中。
resultList.add(mid);
return resultList;
}
}
//以下這段代碼來自百度百科,供大傢參考。
public static int binarySearch(Integer[] srcArray, int des) {
//定義初始最小、最大索引
int start = 0;
int end = srcArray.length - 1;
//確保不會出現重復查找,越界
while (start <= end) {
//計算出中間索引值
int middle = (end + start)>>>1 ;//防止溢出
if (des == srcArray[middle]) {
return middle;
//判斷下限
} else if (des < srcArray[middle]) {
end = middle - 1;
//判斷上限
} else {
start = middle + 1;
}
}
//若沒有,則返回-1
return -1;
}
}
循環實現代碼(非遞歸)
package search;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* @Author: sshdg
* @Date: 2020/9/21 9:22
*/
public class BinarySearch2 {
public static void main(String[] args) {
int[] array = {1,1,1,1,1,2,3,4,5,6,7};
System.out.println(BinarySearch2.binarySearch(array, 7));
}
public static List<Integer> binarySearch(int[] array, int key){
List<Integer> resultList = new ArrayList<>();
int start = 0;
int end = array.length - 1;
while (start <= end){
int mid = (start + end) / 2;
int midValue = array[mid];
if (key > midValue){
//key比中間值大。向右找
start = mid + 1;
} else if (key < midValue){
//key比中間值小。向左找
end = mid - 1;
} else {
//否則就找到瞭
//先向左找有沒有相同值
int temp = mid -1;
while (temp >= start && array[temp] == key){
resultList.add(temp);
temp -= 1;
}
//將一開始找到的加入結果集
resultList.add(mid);
//再向右找找有沒有相同值
temp = mid + 1;
while (temp <= end && array[temp] == key){
resultList.add(temp);
temp += 1;
}
break;
}
}
return resultList;
}
}
二分法查找(遞歸、循環)
public class BinarySearch {
/**
* @author JadeXu
* @// TODO: 2020/12/7 二分查找
* 思路:
* 1、獲取數組的中間值,先獲取下標,方便多次查找
* 奇數位的數組直接獲取中間位,偶數位的數組獲取中間的第一位或第二位都可,一般獲取第一位(因為與奇數位獲取中間值的方法一樣)
* 2、獲取查找的區間范圍,start:區間開始的下標,end:區間結束的下標
* 3、判斷查找的數和中間位的數是否相同
* 相同時,直接返回需要的數據,跳出方法
* 大於時,即數可能在中間值右邊的區間內,此時start = mid+1,即mid往後移一位,就得到瞭中間值右邊區間的開始下標
* 小於時,即數可能在中間值左邊的區間內,此時end = mid-1,即mid往前移一位,就得到瞭中間值左邊區間的結束下標
* 當一個區間裡,開始下標小於等於結束下標時,該區間才是有效區間,才能繼續查找。否則無效,返回找不到,跳出方法
*/
//循環
/**
* @param arr 已經升序好的int[]
* @param num 需要查找的數字
* @return 找到則返回下標,沒找到則返回-1
*/
private static int binarySearchByCycle(int[] arr,int num) {
int start = 0;
int end = arr.length - 1;
while (start <= end){
int mid = (start + end) / 2;
if(num == arr[mid]){
return mid;
}else if(num > arr[mid]){
start = mid + 1;
}else {
end = mid - 1;
}
}
return -1;
}
//遞歸
/**
* @param arr 已經升序好的int[]
* @param num 需要查找的數字
* @param start 區間開始下標
* @param end 區間結束下標
* @return 找到則返回下標,沒找到則返回-1
*/
private static int binarySearchByRecursion(int[] arr,int num,int start,int end) {
int mid = (start + end) / 2;
if(num == arr[mid]){
return mid;
}else if(num > arr[mid]){
start = mid + 1;
}else {
end = mid - 1;
}
if(start <= end){
mid = binarySearchByRecursion(arr,num,start,end); //遞歸繼續尋找
}else {
mid = -1;
}
return mid;
}
}
以上為個人經驗,希望能給大傢一個參考,也希望大傢多多支持WalkonNet。