C++實現LeetCode(119.楊輝三角之二)

Posted on by

[LeetCode] 119. Pascal’s Triangle II 楊輝三角之二

Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal’s triangle.

Note that the row index starts from 0.


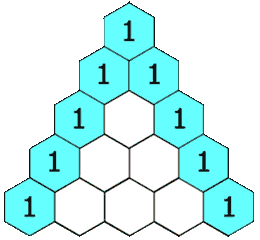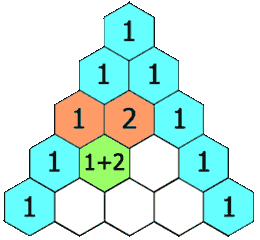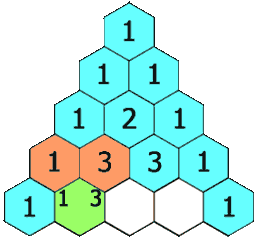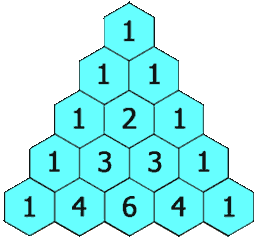
In Pascal’s triangle, each number is the sum of the two numbers directly above it.

Example:

Input: 3
Output: [1,3,3,1]

Follow up:

Could you optimize your algorithm to use only O(k) extra space?

楊輝三角想必大傢並不陌生，應該最早出現在初高中的數學中，其實就是二項式系數的一種寫法。

　　　　　　　　１
１　１
１　２　１
１　３　３　１
１　４　６　４　１
１　５　10　10　５　１
１　６　15　20　15　６　１
１　７　21　35　35　21　７　１
１　８　28　56　70　56　28　８　１

楊輝三角形第n層（頂層稱第0層，第1行，第n層即第 n+1 行，此處n為包含0在內的自然數）正好對應於二項式 \left(a+b\right)^{n} 展開的系數。例如第二層 1 2 1 是冪指數為2的二項式\left(a+b\right)^{2} 展開形式a^{2}+2ab+b^{2} 的系數。

由於題目有額外限制條件，程序隻能使用 O(k) 的額外空間，那麼這樣就不能把每行都算出來，而是要用其他的方法, 我最先考慮用的是第三條性質，算出每個組合數來生成第n行系數。本地調試輸出前十行，沒啥問題，拿到 OJ 上測試，程序在第 18 行跪瞭，中間有個系數不正確。那麼問題出在哪瞭呢，仔細找找，原來出在計算組合數那裡，由於算組合數時需要算連乘，而整型數 int 的數值范圍隻有 -32768 到 32768 之間，那麼一旦n值過大，連乘肯定無法計算。而喪心病狂的 OJ 肯定會測試到成百上千行，所以這個方法不行。那麼我們再來考慮利用第五條性質，除瞭第一個和最後一個數字之外，其他的數字都是上一行左右兩個值之和。那麼我們隻需要兩個 for 循環，除瞭第一個數為1之外，後面的數都是上一次循環的數值加上它前面位置的數值之和，不停地更新每一個位置的值，便可以得到第n行的數字，具體實現代碼如下：

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> res(rowIndex + 1);
        res[0] = 1;
        for (int i = 1; i <= rowIndex; ++i) {
            for (int j = i; j >= 1; --j) {
                res[j] += res[j - 1];
            }
        }
        return res;
    }
};

Github 同步地址：

https://github.com/grandyang/leetcode/issues/119

類似題目：

Pascal’s Triangle

參考資料：

https://leetcode.com/problems/pascals-triangle-ii/

https://leetcode.com/problems/pascals-triangle-ii/discuss/38420/Here-is-my-brief-O(k)-solution

https://leetcode.com/problems/pascals-triangle-ii/discuss/38478/My-accepted-java-solution-any-better-code

到此這篇關於C++實現LeetCode(119.楊輝三角之二)的文章就介紹到這瞭,更多相關C++實現楊輝三角之二內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet！

推薦閱讀：