Python程序流程控制實驗
1. 編寫程序計算 1+3+5+7…+99 之和。
sum=0 for i in range(1,100,2): sum+=i print(sum)
2. 編寫程序,計算 2+4+6+8…+100 之和。
sum=0 for i in range(2,101,2): sum+=i print(sum)
3. 編寫程序,使用不同的實現方法輸出 2000~3000 的所有閏年,運行效果如下圖所示。
num=0 for i in range(2000,3001): if (i%4==0 and i%100!=0) or i%400==0: num+=1 if num%8==0: print(i,end='\n') else: print(i,end='\t') else: i=i+1
4. 編寫程序,計算 Sn=1-3+5-7+9-11+……n
n=int(input('請輸入n的值:'))
##方法一:
Sn = 0
x = -1
for i in range(0,n+1):
if i % 2==0: #是偶數
x=-x
else:
Sn+=i*x
print('Sn=',Sn)
###方法二:
sum1=0
sum2=0
for j in range(1,n+1,4):
sum1+=j
for k in range(3,n+1,4):
sum2+=k
Sn=sum1-sum2
print('Sn=',Sn)
5. 編寫程序,計算 Sn=1+1/2+1/3+…1/n
n=int(input('請輸入n的值:'))
x=1
sum=0
for i in range(1,n+1,1):
x=1/i
sum+=x
print('Sn={:2.2f}'.format(sum))
6.編寫程序,打印九九乘法表。(隻要實現四種方式中的一種即可)
要求輸出九九乘法表的各種顯示效果(上三角、下三角、矩形塊等方式)
for i in range(1,10):
for j in range(1,11-i):
print("{0}*{1}={2}".format((10-i),j,(10-i)*j),end='\t')
print(end='\n')
for i in range(1,10):
for j in range(1,i+1):
print("{0}*{1}={2}".format(i,j,i*j),end='\t')
print(end='\n')
7. 編寫程序輸入三角形的3條邊,先判斷是否可以構成三角形,如果可以,則進一步求三角形的周長和面積,否則報錯“無法構成三角形!”。
其運行效果如圖下圖所示(結果均保留位小數):

import math
a=float(input('請輸入三角形的邊長a:'))
b=float(input('請輸入三角形的邊長b:'))
c=float(input('請輸入三角形的邊長c:'))
print('三角形三邊分別為:a={0},b={1},c={2}'.format(a,b,c))
l=a+b+c
h=l/2
area=math.sqrt(h*(h-a)*(h-b)*(h-c))
if a>0 and b>0 and c>0 and a+b>c and a+c>b and b+c>a:
print('三角形的周長={0}'.format(l))
print('三角形的面積={0}'.format(area))
else:
print('無法構成三角形!')
8. 編寫程序,輸入 x,根據如下公式計算分段函數 y 的值。請分別利用單分支語句雙分支結構以及條件運算語句等方法實現。
import math
x = float(input('請輸入X:'))
if x >= 0: y = (x * x - 3 * x) / (x + 1) + 2 * math.pi + math.sin(x)
if x < 0: y = math.log(-5 * x) + 6 * math.sqrt((-x + math.e ** 4)) - (x + 1) ** 3
print('方法一:x={0}, y={1}'.format(x, y)) # 一句單分支會導致錯誤
print('方法二:x={0}, y={1}'.format(x, y))
if x >= 0:
y = (x * x - 3 * x) / (x + 1) + 2 * math.pi + math.sin(x)
else:
y = math.log(-5 * x) + 6 * math.sqrt((-x + math.e ** 4)) - (x + 1) ** 3
print('方法三:x={0}, y={1}'.format(x, y))
y = (x * x - 3 * x) / (x + 1) + 2 * math.pi + math.sin(x) if (x >= 0) else \
math.log(-5 * x) + 6 * math.sqrt((-x + math.e ** 4)) - (x + 1) ** 3
print('方法四:x={0}, y={1}'.format(x, y))
9. 編寫程序,輸入一元二次方程的 3 個系數 a、b 和 c,求 ax²+bx+c=0 方程的解。結果如下圖所示
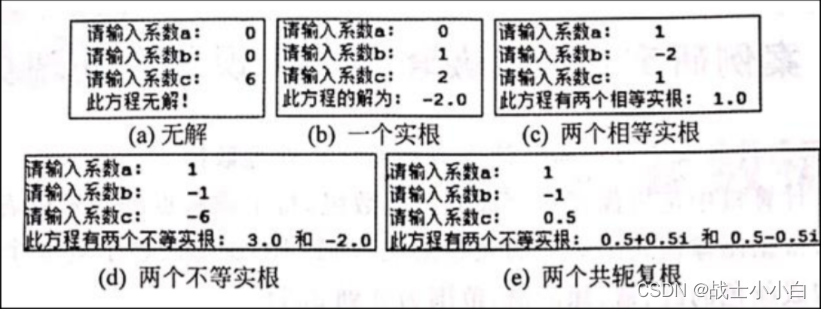
import math
a=float(input('請輸入系數a:'))
b=float(input('請輸入系數b:'))
c=float(input('請輸入系數c:'))
d=b*b-4*a*c #判別式
if a==0 and b==0:
print('此方程無解!')
elif a==0 and b!=0:
print('此方程的解為:',end='')
x=-c/b
print(x)
elif d==0: #判別式等於0
print('此方程有兩個相等實根:',end='')
x=(-b)/2*a
print(x)
elif d>0: #判別式大於0
print('此方程有兩個不等實根:',end='')
x1=((-b)+math.sqrt(d))/2*a
x2=((-b)- math.sqrt(d))/2*a
print(x1,' 和 ',x2)
elif d<0: #判別式小於0
print('此方程有兩個共軛復根:',end='')
real=(-b)/2*a #實部
imag=(math.sqrt(-d))/2*a #虛部
x1=complex(real,imag)
x2=complex(real,-imag)
print(x1,' 和 ',x2)
10. 編寫程序,輸入整數 n(n≥0),分別利用 for 循環和 while循環求 n!。
n=int(input('請輸入整數n:'))
s=1
if n<0:
n = int(input('請輸入非負整數:'))
elif n == 0:
print('0!=1')
else:
for i in range(1, n + 1):
s *= i
print(str.format(' for循環:{}!={}', n, s))
s = i = 1
while i <= n:
s *= i
i += 1
print(str.format('while循環:{}!={}', n, s))
11.編寫程序,產生兩個 0~100(包含 0 和 100)的隨機整數 a 和 b,求這兩個整數的最大公約數和最小公倍數。
import random
a=random.randint(0,100)
b=random.randint(0,100)
print(str.format('整數a={},整數b={}',a,b))
if a<b:
a,b=b,a
n1=a
n2=b
while(n2!=0): #輾轉相除法
t=n1 % n2
n1=n2
n2=t
print("最大公約數:",n1)
print("最小公倍數:",int(a*b/n1))
import random
a = random.randint(0, 100)
b = random.randint(0, 100)
def gcd(x, y):
return x if y == 0 else gcd(y,x%y)
print(str.format('整數a={},整數b={}',a,b))
print(str.format('最大公約數={},最小公倍數={}',gcd(a,b),int(a*b/gcd(a,b))))
到此這篇關於Python程序流程控制實驗的文章就介紹到這瞭,更多相關Python程序流程控制內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!