numpy稀疏矩陣的實現
1. coo存儲方式
采用三元組(row, col, data)(或稱為ijv format)的形式來存儲矩陣中非零元素的信息。
coo_matrix的優點:有利於稀疏格式之間的快速轉換(tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil();允許重復項(格式轉換的時候自動相加);能與CSR / CSC格式的快速轉換
coo_matrix的缺點:不能直接進行算術運算,包括賦值
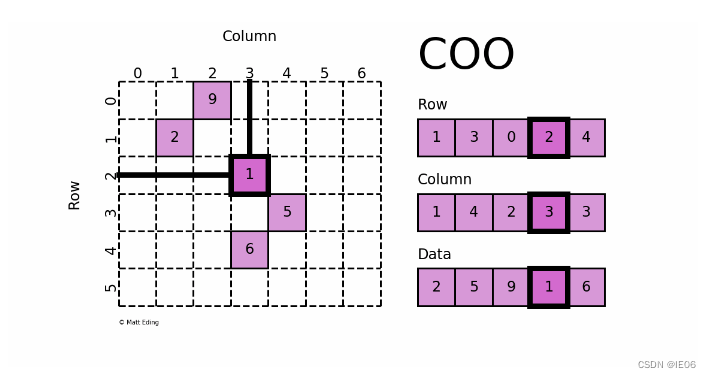
初始化方式:
coo_matrix(D), D代表密集矩陣
賦值:
>>> import numpy as np
>>> from scipy.sparse import coo_matrix
>>> _row = np.array([0, 3, 1, 0])
>>> _col = np.array([0, 3, 1, 2])
>>> _data = np.array([4, 5, 7, 9])
>>> coo = coo_matrix((_data, (_row, _col)), shape=(4, 4), dtype=np.int)
>>> coo.todense() # 通過toarray方法轉化成密集矩陣(numpy.matrix)
>>> coo.toarray() # 通過toarray方法轉化成密集矩陣(numpy.ndarray)
array([[4, 0, 9, 0],
[0, 7, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 5]])
2. dok_matrix
dok_matrix,即Dictionary Of Keys based sparse matrix,是一種類似於coo matrix但又基於字典的稀疏矩陣存儲方式,key由非零元素的的坐標值tuple(row, column)組成,value則代表數據值。dok matrix非常適合於增量構建稀疏矩陣,並一旦構建,就可以快速地轉換為coo_matrix。
>>> import numpy as np
>>> from scipy.sparse import dok_matrix
>>> np.random.seed(10)
>>> matrix = random(3, 3, format='dok', density=0.4)
>>> matrix[1, 1] = 33
>>> matrix[2, 1] = 10
>>> matrix.toarray()
array([[ 0. , 0. , 0. ],
[ 0. , 33. , 0. ],
[ 0.19806286, 10. , 0.22479665]])
>>> dict(matrix)
{(2, 0): 0.19806286475962398, (2, 1): 10.0, (2, 2): 0.22479664553084766, (1, 1): 33.0}
>>> isinstance(matrix, dict)
True
3. csr和csc存儲方式
csr_matrix,全稱Compressed Sparse Row matrix,即按行壓縮的稀疏矩陣存儲方式,由三個一維數組indptr, indices, data組成。這種格式要求矩陣元「按行順序存儲」,「每一行中的元素可以亂序存儲」。那麼對於每一行就隻需要用一個指針表示該行元素的起始位置即可。indptr存儲每一行數據元素的起始位置,indices這是存儲每行中數據的列號,與data中的元素一一對應。
csr_matrix,是按列壓縮,不再贅述

csr_matrix的優點:
高效的算術運算CSR + CSR,CSR * CSR等
高效的行切片
快速矩陣運算
csr_matrix的缺點:
列切片操作比較慢(考慮csc_matrix)
稀疏結構的轉換比較慢(考慮lil_matrix或doc_matrix)
>>> import numpy as np
>>> from scipy.sparse import csr_matrix
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csr = csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]])
4. lil_matrix
lil_matrix,即List of Lists format,又稱為Row-based linked list sparse matrix。它使用兩個嵌套列表存儲稀疏矩陣:data保存每行中的非零元素的值,rows保存每行非零元素所在的列號(列號是順序排序的)。
LIL matrix本身的設計是用來方便快捷構建稀疏矩陣實例,而算術運算、矩陣運算則轉化成CSC、CSR格式再進行,構建大型的稀疏矩陣還是推薦使用COO格式。

5. dia_matrix
dia_matrix,全稱Sparse matrix with DIAgonal storage,是一種對角線的存儲方式。如下圖中,將稀疏矩陣使用offsets和data兩個矩陣來表示。

>>> data = np.arange(15).reshape(3, -1) + 1
>>> offsets = np.array([0, -3, 2])
>>> dia = sparse.dia_matrix((data, offsets), shape=(7, 5))
>>> dia.toarray()
array([[ 1, 0, 13, 0, 0],
[ 0, 2, 0, 14, 0],
[ 0, 0, 3, 0, 15],
[ 6, 0, 0, 4, 0],
[ 0, 7, 0, 0, 5],
[ 0, 0, 8, 0, 0],
[ 0, 0, 0, 9, 0]])
6. 稀疏矩陣經驗
要有效地構造矩陣,請使用dok_matrix或lil_matrix
lil_matrix類支持基本切片和花式索引,其語法與NumPy Array類似;lil_matrix形式是基於row的,因此能夠很高效的轉為csr,但是轉為csc效率相對較低。
要執行乘法或轉置等操作,首先將矩陣轉換為CSC或CSR格式,效率高
CSR格式特別適用於快速矩陣矢量產品
CSR,CSC和COO格式之間的所有轉換都是線性復雜度。
到此這篇關於numpy稀疏矩陣的實現的文章就介紹到這瞭,更多相關numpy 稀疏矩陣內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!
推薦閱讀:
- 初識python的numpy模塊
- python中NumPy的安裝與基本操作
- R語言rhdf5讀寫hdf5並展示文件組織結構和索引數據
- python數學建模(SciPy+ Numpy+Pandas)
- Python Numpy中ndarray的常見操作