python實現高斯模糊及原理詳解

Posted on by

高斯模糊是一種常見的模糊技術，相關知識點有：高斯函數、二維卷積。

圖片

 （一）一維高斯分佈函數

一維（連續變量）高斯函數形式如下，高斯函數又稱“正態分佈函數”：

圖片

μ是分佈函數的均值（或者期望），sigma是標準差。

一維高斯分佈函數的圖形：

從圖可知，以x=0為中心，x取值距離中心越近，概率密度函數值越大，距離中心越遠，密度函數值越小。

（二）二維高斯分佈函數

二維高斯分佈函數的形式：

特別說明，當變量x和y相互獨立時，則相關系數ρ=0，二維高斯分佈函數可以簡化為：

二維高斯分佈函數的圖形：

圖片

對於一維高斯分佈，函數中心是平面上的一個點；而對於二維高斯分佈，函數中心是一個三維立體空間上的一個點，即上圖中山峰的最頂端處的點。

（三）高斯模糊

高斯模糊本質上一種數據平滑技術，可以用於一維、二維甚至多維空間。數據經高斯模糊處理之後，數據會趨向於周邊鄰近的其他數據，導致各個數據“趨同”。

在圖像領域，各個位置的像素值使用“周邊鄰居像素點加權平均”重新賦值。對於每個像素點，由於計算時均以當前像素點為中心，所以均值μ=0。使用時有2個超參數需要設置：高斯核大小和高斯函數標準差σ。高斯核大小表示“影響當前點的最大鄰域范圍”，而標準差表示“鄰域中的其他像素點對當前點的影響力”。

從下而上觀察下圖各個函數圖像，各個函數的均值相同，而方差逐步減小。

圖片

方差衡量數據的分散程度，方差越大，數據越分散，圖形就越扁平，數據的集中趨勢越弱，應用到高斯模糊中方差越大圖形越模糊。

高斯模糊涉及到2個關鍵技術點：

（1）如何計算高斯卷積核

3×3大小的高斯卷積核的計算示意圖

圖片

直接計算二維高斯函數值後，卷積核的各個位置取值（截圖自pycharm的debug）：

圖片

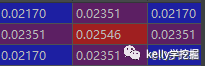
卷積核歸一化後的各個位置取值（截圖自pycharm的debug）：

高斯卷積核的python代碼：

def gaussian_kernel(self):
	kernel = np.zeros(shape=(self.kernel_size, self.kernel_size), dtype=np.float)
	radius = self.kernel_size//2
	for y in range(-radius, radius + 1):  # [-r, r]
		for x in range(-radius, radius + 1):
			# 二維高斯函數
			v = 1.0 / (2 * np.pi * self.sigma ** 2) * np.exp(-1.0 / (2 * self.sigma ** 2) * (x ** 2 + y ** 2))
			kernel[y + radius, x + radius] = v  # 高斯函數的x和y值 vs 高斯核的下標值
	kernel2 = kernel / np.sum(kernel)
	return kernel2

（2）如何在二維圖像上進行卷積

對於二維矩陣，卷積時卷積核從左向右、從上而下的滑動，對應位置求加權和。一般圖像是RGB三通道，需要逐個通道卷積，每個通道是一個二維矩陣。灰度圖隻有一個通道，直接卷積即可。

自行實現的二維離散卷積的python代碼：

def my_conv2d(inputs: np.ndarray, kernel: np.ndarray):
    # 計算需要填充的行列數目，這裡假定mode為“same”
    # 一般卷積核的hw都是奇數，這裡實現方式也是基於奇數尺寸的卷積核
    h, w = inputs.shape
    kernel = kernel[::-1, ...][..., ::-1]  # 卷積的定義，必須旋轉180度
    h1, w1 = kernel.shape
    h_pad = (h1 - 1) // 2
    w_pad = (w1 - 1) // 2
    inputs = np.pad(inputs, pad_width=[(h_pad, h_pad), (w_pad, w_pad)], mode="constant", constant_values=0)
    outputs = np.zeros(shape=(h, w))
    for i in range(h):  # 行號
        for j in range(w):  # 列號
            outputs[i, j] = np.sum(np.multiply(inputs[i: i + h1, j: j + w1], kernel))
    return outputs

scipy中已經提供二維卷積函數scipy.signal.convolve2d，可以直接調用，下圖是和自行實現的對比效果。

圖片

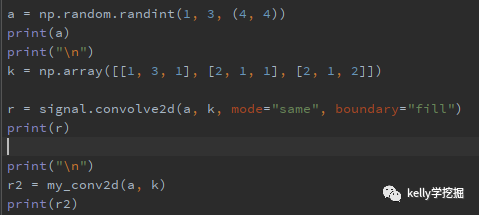
 運行之後結果一致，驗證自行實現的二維卷積正確。

圖片

補充：scipy.signal.convolve2d的參數說明

in1：輸入矩陣

in2：卷積核

mode：指示輸出矩陣的尺寸，full代表完全離散線性卷積, valid代表輸出尺寸等於輸入尺寸-卷積核+1, same代表輸出尺寸與輸入尺寸一致。

boundary：需要填充時邊界填充方式，fill代表使用常量值填充, wrap代表循環方式填充, symm代表以四周邊為對稱軸對稱填充。

fillvalue：常量填充時的填充值

（四）完整代碼和運行效果

完整的python代碼​​​​​​

 
class GaussianBlur(object):
    def __init__(self, kernel_size=3, sigma=1.5):
        self.kernel_size = kernel_size
        self.sigma = sigma
        self.kernel = self.gaussian_kernel()
 
    def gaussian_kernel(self):
        kernel = np.zeros(shape=(self.kernel_size, self.kernel_size), dtype=np.float)
        radius = self.kernel_size//2
        for y in range(-radius, radius + 1):  # [-r, r]
            for x in range(-radius, radius + 1):
                # 二維高斯函數
                v = 1.0 / (2 * np.pi * self.sigma ** 2) * np.exp(-1.0 / (2 * self.sigma ** 2) * (x ** 2 + y ** 2))
                kernel[y + radius, x + radius] = v  # 高斯函數的x和y值 vs 高斯核的下標值
        kernel2 = kernel / np.sum(kernel)
        return kernel2
 
    def filter(self, img: Image.Image):
        img_arr = np.array(img)
        if len(img_arr.shape) == 2:
            new_arr = signal.convolve2d(img_arr, self.kernel, mode="same", boundary="symm")
        else:
            h, w, c = img_arr.shape
            new_arr = np.zeros(shape=(h, w, c), dtype=np.float)
            for i in range(c):
                new_arr[..., i] = signal.convolve2d(img_arr[..., i], self.kernel, mode="same", boundary="symm")
        new_arr = np.array(new_arr, dtype=np.uint8)
        return Image.fromarray(new_arr)
 
 
def main():
    img = Image.open("Jeep-cd.jpg").convert("RGB")
    img2 = GaussianBlur(sigma=2.5).filter(img)
 
    plt.subplot(1, 2, 1)
    plt.imshow(img)
 
    plt.subplot(1, 2, 2)
    plt.imshow(img2)
 
    # dpi參數維持圖片的清晰度
    plt.savefig("gaussian.jpg", dpi=500)
    plt.show()
    pass

代碼運行效果，發現經高斯模糊處理之後，圖片發生明顯模糊。

圖片

 圖片

到此這篇關於python實現高斯模糊及原理詳解的文章就介紹到這瞭,更多相關python 高斯模糊內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet！

推薦閱讀：