pytorch神經網絡從零開始實現多層感知機

Posted on by

我們已經在數學上描述瞭多層感知機，現在讓我們嘗試自己實現一個多層感知機。為瞭與我們之前使用softmax回歸獲得的結果進行比較，我們將繼續使用Fashion-MNIST圖像分類數據集。

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化模型參數

Fashion-MNIST中的每個圖像由 28 × 28 = 784個灰度圖像值組成。所有圖像共分為10個類別。忽略像素之間的空間結構，我們可以將每個圖像視為784個輸入特征和10個類的簡單分類數據集。
首先，我們將實現一個具有單隱藏層的多層感知機，它包含256個隱藏單元。註意我們可以將這兩個量都視為超參數。通常，我們選擇2的若幹次冪作為層的寬度。
我們用幾個張量來表示我們的參數。註意，對於每一層我們都需要記錄一個權重矩陣和一個偏置向量。跟以前一樣，我們要為這些參數的損失梯度分配內存。

num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(torch.randn(
num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]

激活函數

為瞭確保我們知道一切是如何工作的，我們將使用最大值函數自己實現ReLU激活函數，而不是直接調用內置的relu函數。

def relu(X):
	a = torch.zeros_like(X)
	return torch.max(X, a)

模型

因為我們忽略瞭空間結構，所示我們使用reshape將每個二維圖像轉換為一個長度為num_inputs的向量。我們隻需幾行代碼就可以實現我們的模型。

def net(X):
	X = X.reshape((-1, num_inputs))
	H = relu(X@W1 + b1)    # 這裡“@”代表矩陣乘法
	return (H@W2 + b2)

損失函數

為瞭確保數值的穩定性，同時由於我們已經從零實現過softmax函數，因此在這裡我們直接使用高級API中的內置函數來計算softmax和交叉熵損失。

loss = nn.CrossEntropyLoss()

訓練

幸運的是，多層感知機的訓練過程與softmax回歸的訓練過程完全相同。可以直接調用d2l包的train_ch3函數，將迭代周期設置為10，並將學習率設置為0.1。

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

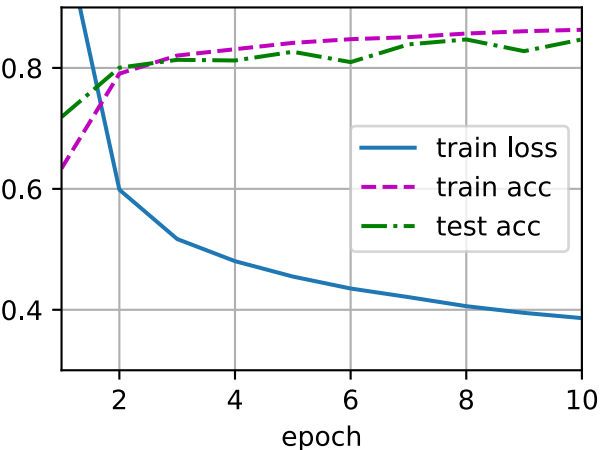
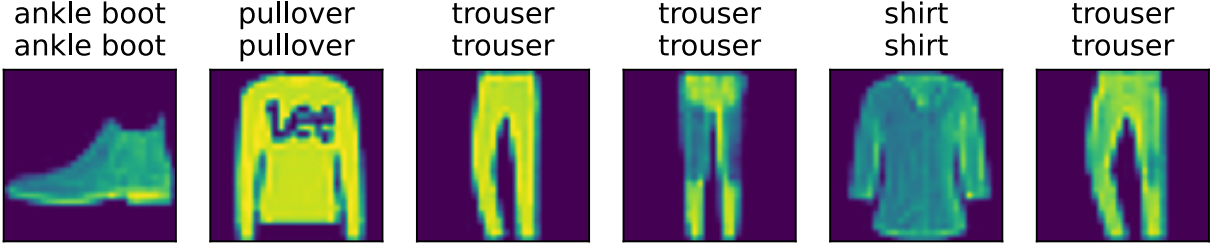
在這裡插入圖片描述

為瞭對學習到的模型進行評估，我們將在一些 測試數據上應用這個模型。

d2l.predict_ch3(net, test_iter)

在這裡插入圖片描述

以上就是pytorch神經網絡從零開始實現多層感知機的詳細內容，更多關於pytorch神經網絡多層感知機的資料請關註WalkonNet其它相關文章！

推薦閱讀：