c++基礎算法動態DP解決CoinChange問題

Posted on by

問題來源

這是Hackerrank上的一個比較有意思的問題，詳見下面的鏈接：

https://www.hackerrank.com/challenges/ctci-coin-change

問題簡述

給定m個不同面額的硬幣，C={c0, c1, c2…cm-1}，找到共有幾種不同的組合可以使得數額為n的錢換成等額的硬幣（每種硬幣可以重復使用）。
比如：給定m=3，C={2,1,3}，n=4，那麼共有4種不同的組合可以換算硬幣

{1,1,1,1}

{1,1,2}

{2,2}

{1,3}

解決方案

基本思路是從硬幣（coins）的角度出發，考慮coins[0]僅使用1次的情況下有幾種組合，coins[0]僅使用2次的情況下有幾種組合，依次類推，直到 (n – coins[0] * 使用次數) < 0 則終止，而每個 (n – coins[0]) 下又可以遞歸 (n – coins[0] – coins[1]) 的情況，直到考慮完所有的硬幣。
這樣說可能還是沒有說清楚，下面以m=3，C={1,2,3}，n=4為例，用圖來說明一下（建議結合程序一起看）。

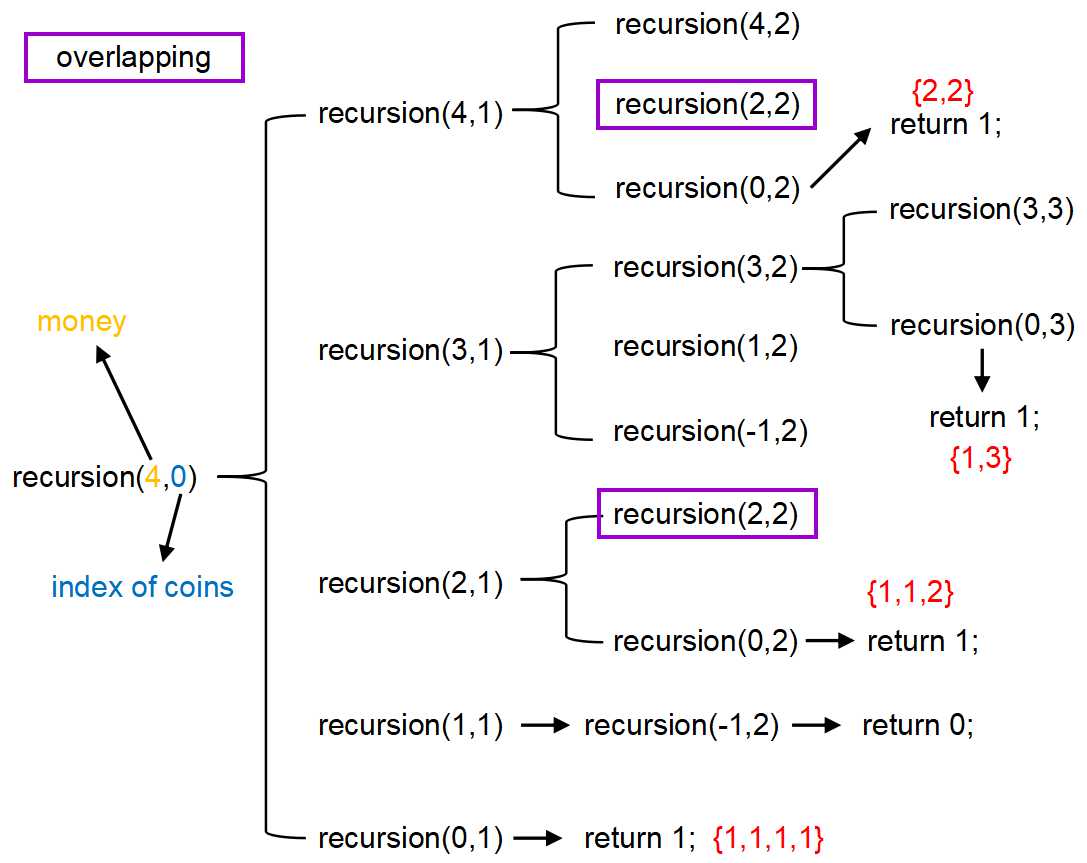
coinChange遞歸圖

圖1：coin Change不完整遞歸圖

上圖沒有畫出完整的遞歸過程（有點麻煩~偷瞭個懶），不過把能得出結果的幾條路徑都描繪出來瞭。其中，recursion(money, index)中，money指的是還沒有進行兌換的錢，index指的是要用哪個coin去兌換，比如這裡的0指的是coins[0]=1，1指的是coins[1]=2，2指的是coins[2]=3，3是不存在的，這也是程序的終止條件之一。 註意到再遞歸的過程中有重疊子問題（我用紫色標註出瞭其中一個），這就可以用動態規劃的思想來解決瞭，創建一塊空間來存儲已經算過的結果就可以瞭。 # 程序代碼 好瞭，下面直接上程序瞭，結合圖看好理解~

#include <iostream>
#include <unordered_map>
#include <string>
#include <vector>
using namespace std;
long long recursion(vector<int> &coins, int money, int index, unordered_map<string, int> &memo){
	//終止條件2個
    if (0 == money)
        return 1;
    if (index >= coins.size() || money < 0)
        return 0;
    string key = to_string(money) + " , " + to_string(index);
    //如果記錄中有的話就直接返回就好瞭
    if (memo.find(key) != memo.end())
        return memo[key];
    long long res = 0;
    int remaining = money;
    while(remaining >= 0){
        res += recursion(coins, remaining, index + 1, memo);
        remaining -= coins[index];
    }
    //記錄一下
    memo[key] = res;
    return res;
}

long long make_change(vector<int> coins, int money) {
	//用哈希表來記錄 <剩下的錢-用的硬幣>:換硬幣的組合數
    unordered_map<string, int> memo;
    long long res = recursion(coins, money, 0, memo);
    return res;
}

int main(){
    int n;
    int m;
    cin >> n >> m;
    vector<int> coins(m);
    for(int coins_i = 0;coins_i < m;coins_i++){
       cin >> coins[coins_i];
    }
    cout << make_change(coins, n) << endl;
    return 0;
}

Sample Input

10 4
2 5 3 6

Sample Output

5

真正的DP

上面的那段代碼是以自頂向下的方式來解決問題的，思路比較清晰，而真正的動態規劃是自底向上的，思路其實也差不多，下面給出代碼~

long long make_change(vector<int> coins, int money) {
    vector<long long> memo(money + 1, 0);
    memo[0] = 1;
    for (int i = 0; i < coins.size(); i++){
        for (int j = coins[i]; j <= money; j++){
            memo[j] += memo[j - coins[i]];
        }
    }
    return memo[money];
}

補充——硬幣不能重復使用

如果每種硬幣不能重復使用的話，又該怎麼辦呢？這隻需要再程序上做一些小的改動就可以瞭，真的是非常神奇~
要細細體會一下~

long long make_change(vector<int> coins, int money) {
	vector<long long> memo(money + 1, 0);
	memo[0] = 1;
	for (int i = 0; i < coins.size(); i++){
		//改動處：由從前往後改成瞭從後往前，略去瞭重復的情況
		for (int j = money; j >= coins[i]; j--){
			memo[j] += memo[j - coins[i]];
		}
	}
	return memo[money];
}

補充2——不同順序表示不同組合

然後再來變一變，如果每種硬幣可以使用無限多次，但是不同的順序表示不同的組合，那麼又有多少種組合呢？
比如：

coins = [1, 2, 3]
money = 4

可能的組合情況有：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

註意，不同的順序序列表示不同的組合~

所以結果是7。

這種情況下的代碼是：

long long make_change(vector<int> coins, int money) {
	vector<long long> memo(money + 1, 0);
	memo[0] = 1;
	//改變瞭裡外循環的順序
	for (int i = 1; i <=money; i++){
		for (int j = 0; j < coins.size(); j++){
			if (i - coins[j] >= 0)
				memo[i] += memo[i - coins[j]];
		}
	}
	return memo[money];
}

要仔細體會一下三種情況下的區別和代碼微妙的變化~

結束語

動態規劃的代碼量其實不大，但是思維量還是挺大的，要寫正確還是要折騰挺久的~
本人是初學者，如有錯誤，還請指正~希望大傢以後多多支持WalkonNet！

推薦閱讀：