python爬蟲實戰steam加密逆向RSA登錄解析
采集目標
網址:steam
工具準備
開發工具:pycharm
開發環境:python3.7, Windows10 使用工具包:requests
項目思路解析
訪問登錄頁面重登錄頁面獲取登錄接口, 先輸入錯誤的賬戶密碼去測試登錄接口。
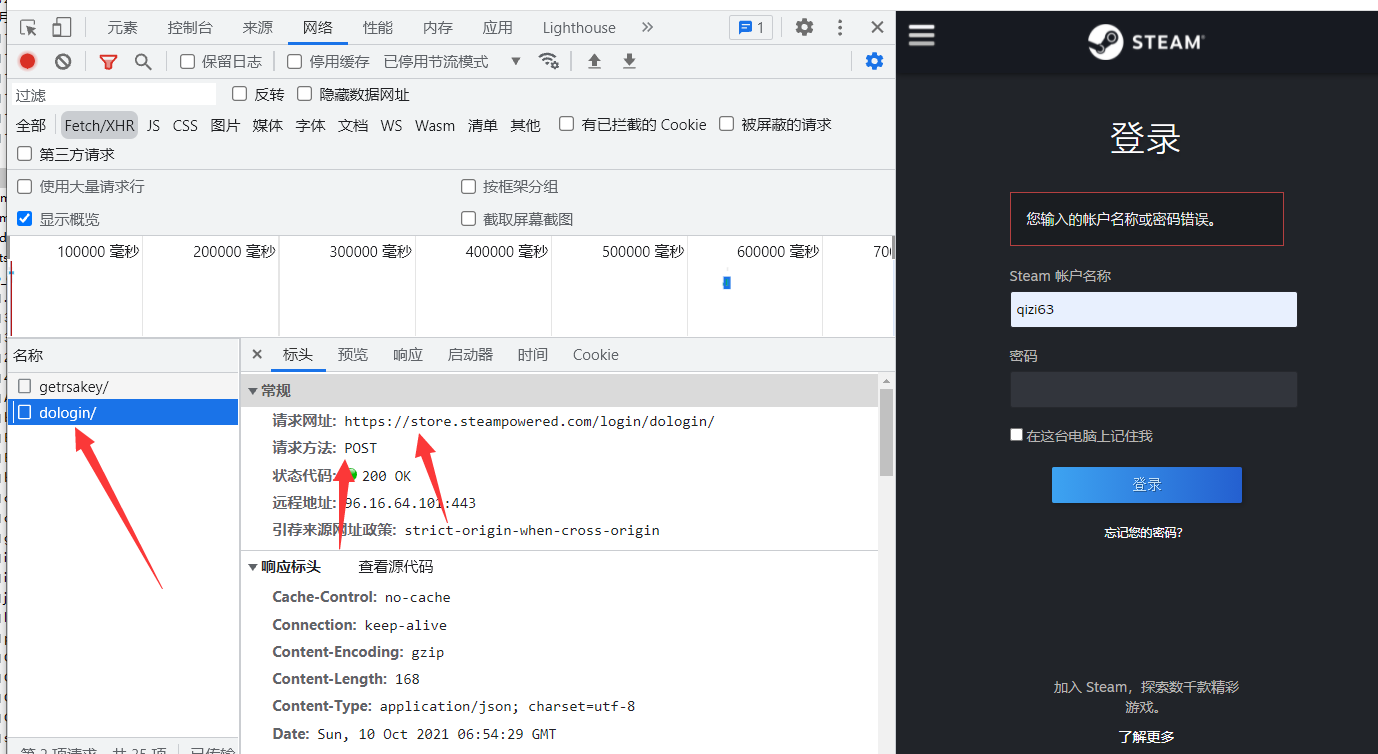
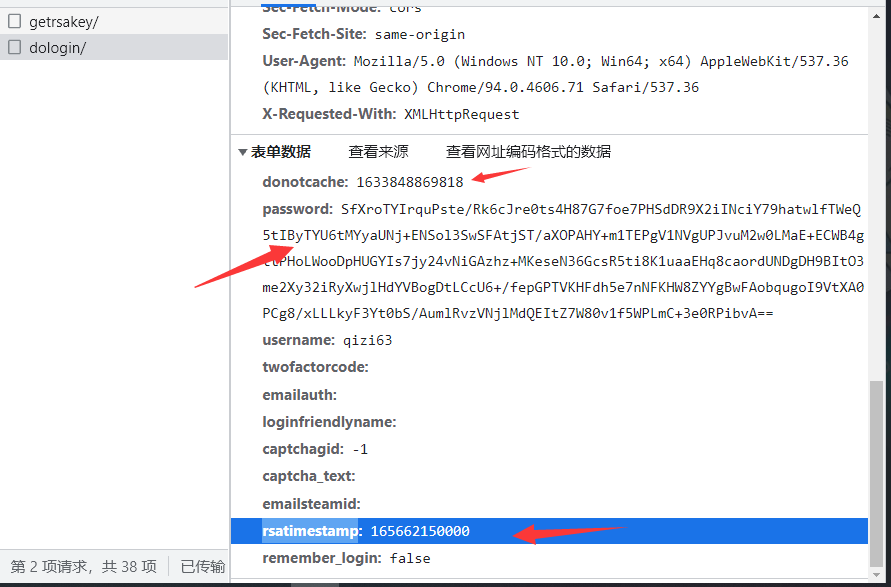
獲取到登錄的接口地址,請求方法是post請求,找到需要傳遞的參數,可以看到密碼數據是加密的第一個數據是時間戳密碼加密字段應該用的base64,rsatimestamp字段目前還不清楚是什麼,其他的都是固定數據。
找到password字段的加密位置,這裡我們直接進行搜索,找加密位置,可以通過名字來大致判斷加密文件。

在文件進行搜索,查看數據值是否存在。
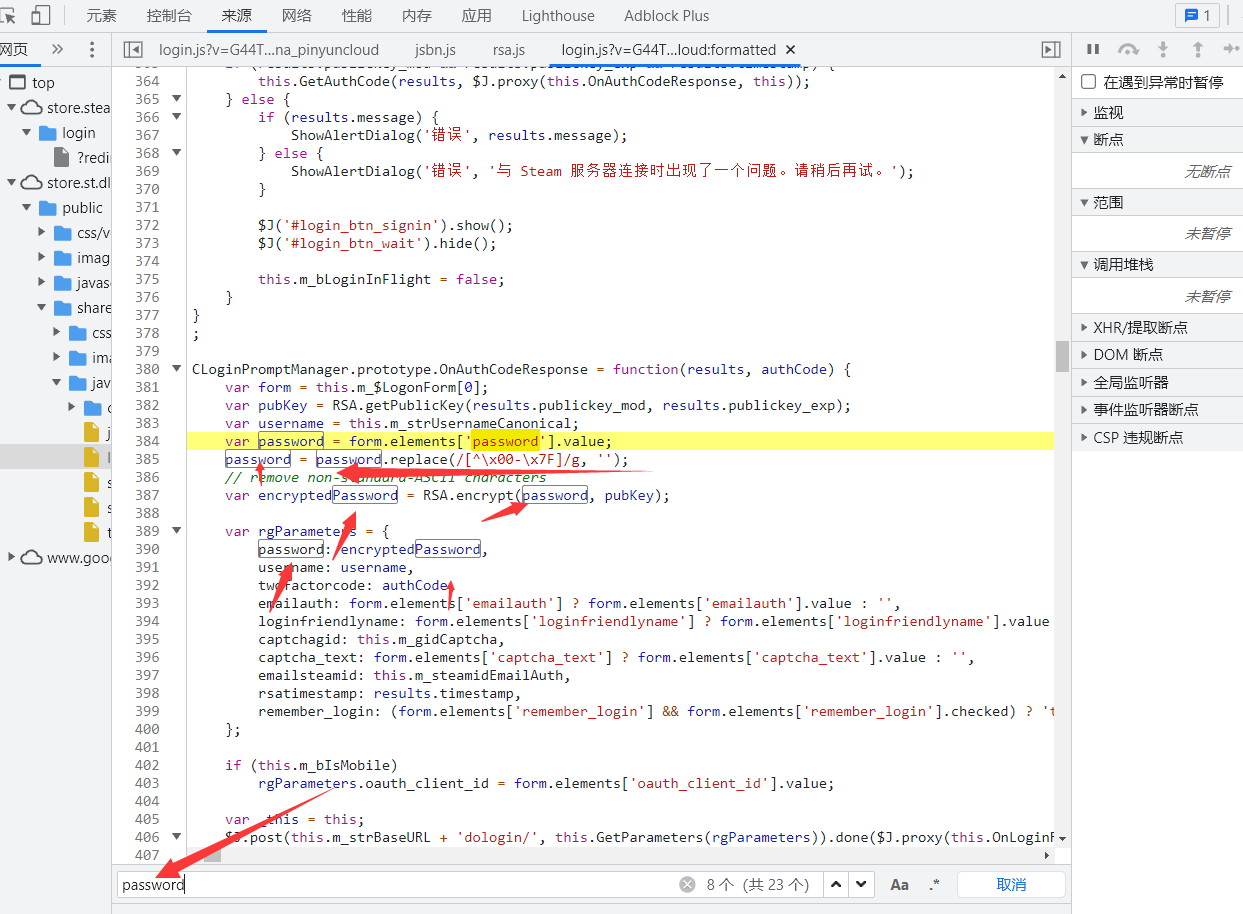
當前可以看出代碼為rsa加密,這裡辣條選擇直接補js環境,先把加密段代碼端進行添加,rsa加密的公秘鑰需要重其他它接口獲取。
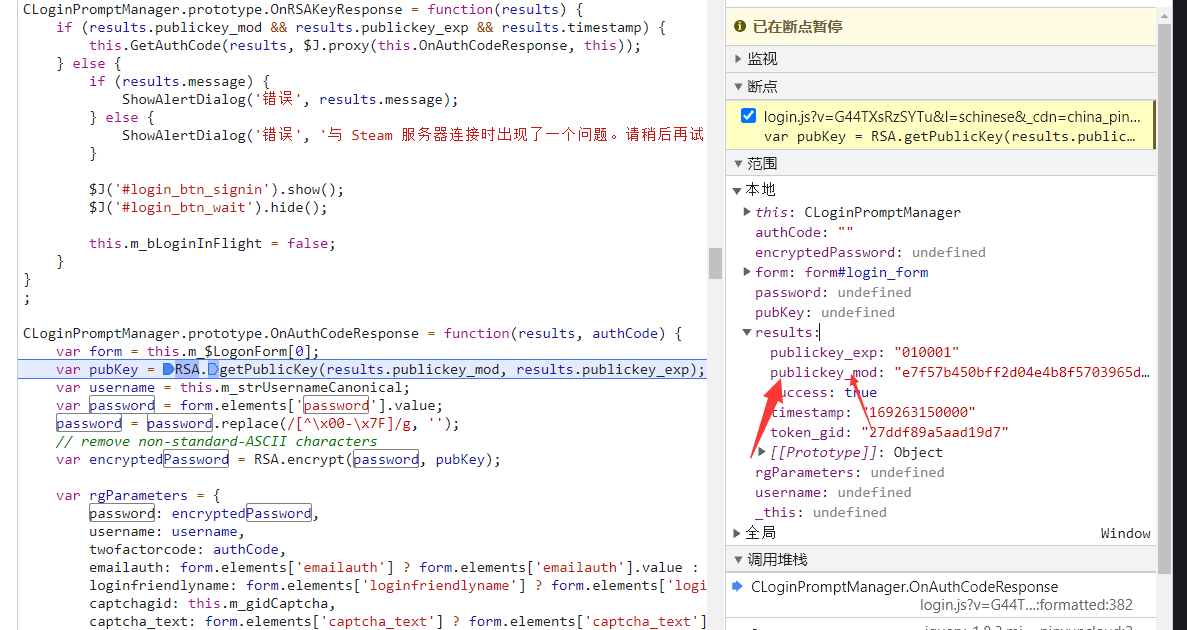
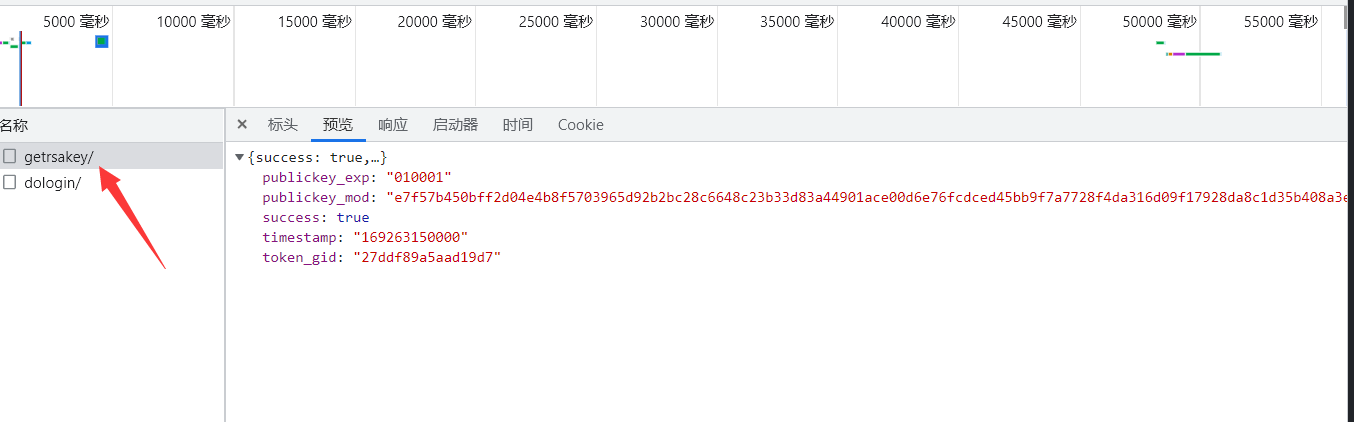
加密的秘鑰以及其他來自這個頁面,需要提取發送請求獲取到,要註意cookie需要保持一致,開始補js環境。
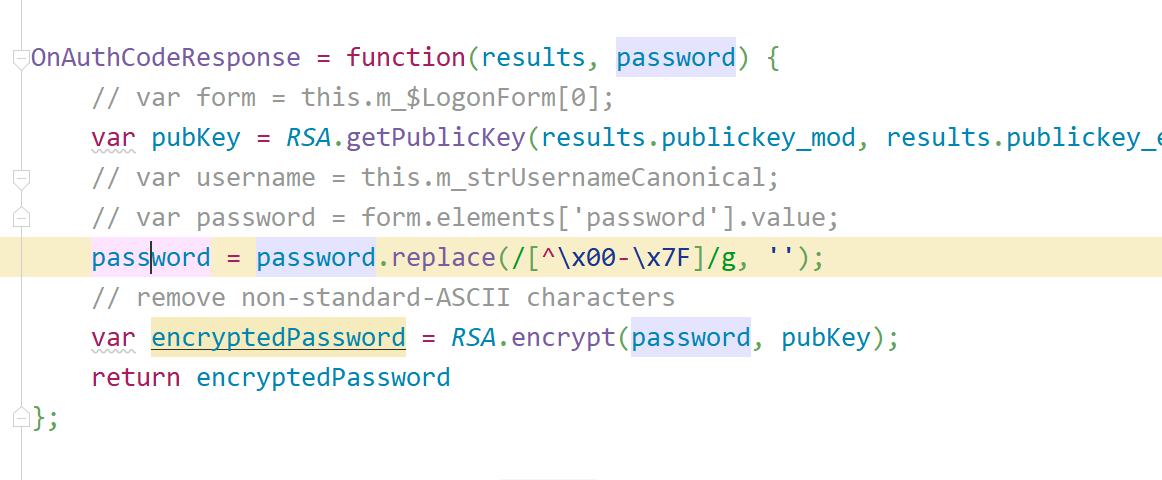
我們不需要賬號信息的獲取,可以直接註釋掉,打印數據,嘗試運行,哪裡報錯補哪裡。
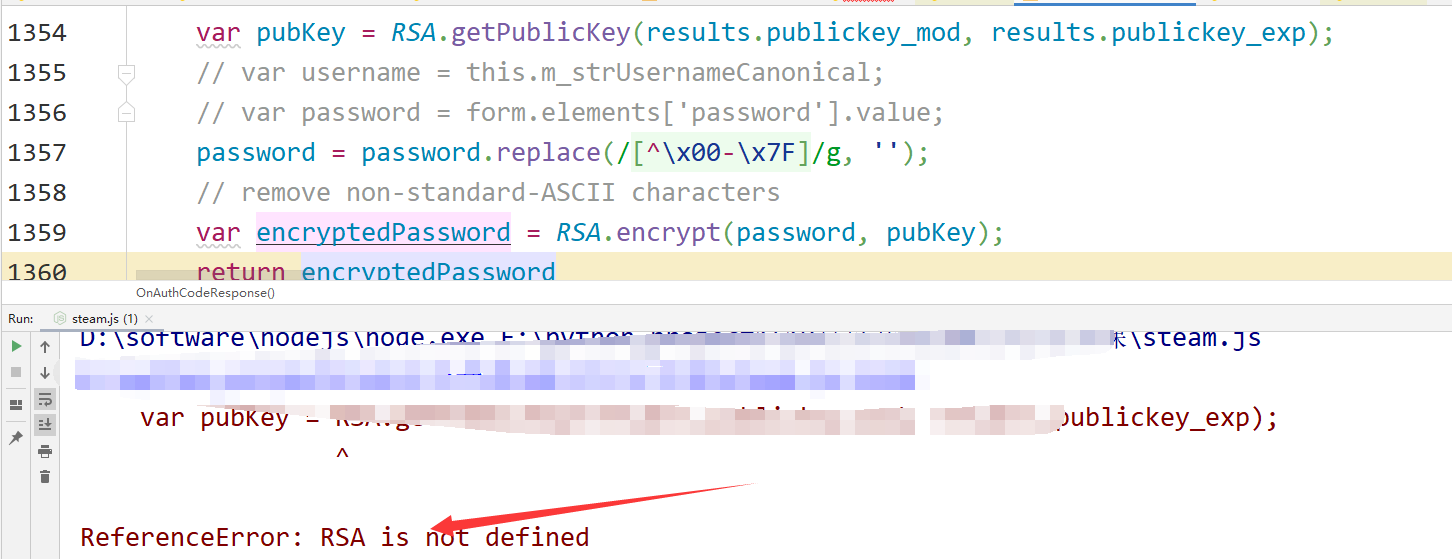
少瞭rsa功能。
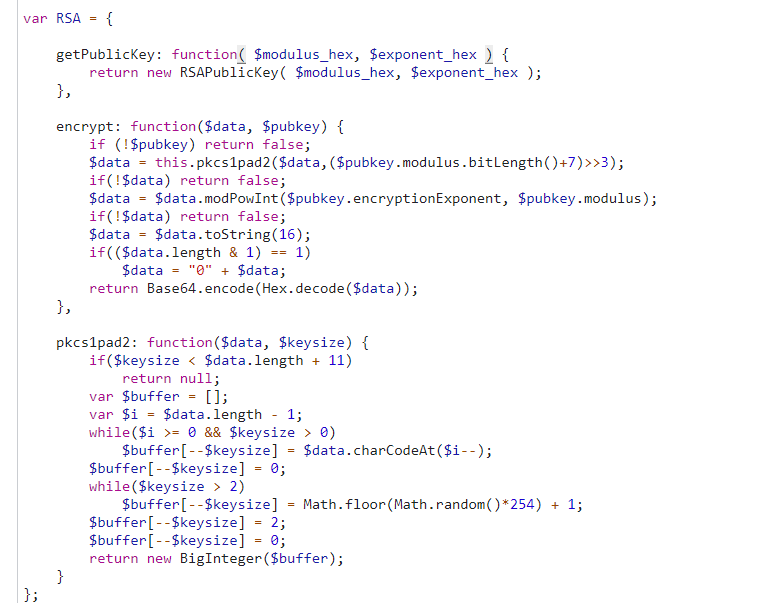
當前文件都拿過來,後面的方法也一樣的直接拿過來就行。
// Copyright (c) 2005 Tom Wu
// All Rights Reserved.
// See "LICENSE" for details.
/*
* Copyright (c) 2003-2005 Tom Wu
* All Rights Reserved.
* Permission is hereby granted, free of charge, to any person obtaining
* a copy of this software and associated documentation files (the
* "Software"), to deal in the Software without restriction, including
* without limitation the rights to use, copy, modify, merge, publish,
* distribute, sublicense, and/or sell copies of the Software, and to
* permit persons to whom the Software is furnished to do so, subject to
* the following conditions:
* The above copyright notice and this permission notice shall be
* included in all copies or substantial portions of the Software.
* THE SOFTWARE IS PROVIDED "AS-IS" AND WITHOUT WARRANTY OF ANY KIND,
* EXPRESS, IMPLIED OR OTHERWISE, INCLUDING WITHOUT LIMITATION, ANY
* WARRANTY OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE.
* IN NO EVENT SHALL TOM WU BE LIABLE FOR ANY SPECIAL, INCIDENTAL,
* INDIRECT OR CONSEQUENTIAL DAMAGES OF ANY KIND, OR ANY DAMAGES WHATSOEVER
* RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER OR NOT ADVISED OF
* THE POSSIBILITY OF DAMAGE, AND ON ANY THEORY OF LIABILITY, ARISING OUT
* OF OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
* In addition, the following condition applies:
* All redistributions must retain an intact copy of this copyright notice
* and disclaimer.
*/
// Basic JavaScript BN library - subset useful for RSA encryption.
// Bits per digit
var dbits;
// JavaScript engine analysis
var canary = 0xdeadbeefcafe;
var j_lm = ((canary&0xffffff)==0xefcafe);
// (public) Constructor
function BigInteger(a,b,c) {
if(a != null)
if("number" == typeof a) this.fromNumber(a,b,c);
else if(b == null && "string" != typeof a) this.fromString(a,256);
else this.fromString(a,b);
}
// return new, unset BigInteger
function nbi() { return new BigInteger(null); }
// am: Compute w_j += (x*this_i), propagate carries,
// c is initial carry, returns final carry.
// c < 3*dvalue, x < 2*dvalue, this_i < dvalue
// We need to select the fastest one that works in this environment.
// am1: use a single mult and divide to get the high bits,
// max digit bits should be 26 because
// max internal value = 2*dvalue^2-2*dvalue (< 2^53)
function am1(i,x,w,j,c,n) {
while(--n >= 0) {
var v = x*this[i++]+w[j]+c;
c = Math.floor(v/0x4000000);
w[j++] = v&0x3ffffff;
}
return c;
}
// am2 avoids a big mult-and-extract completely.
// Max digit bits should be <= 30 because we do bitwise ops
// on values up to 2*hdvalue^2-hdvalue-1 (< 2^31)
function am2(i,x,w,j,c,n) {
var xl = x&0x7fff, xh = x>>15;
while(--n >= 0) {
var l = this[i]&0x7fff;
var h = this[i++]>>15;
var m = xh*l+h*xl;
l = xl*l+((m&0x7fff)<<15)+w[j]+(c&0x3fffffff);
c = (l>>>30)+(m>>>15)+xh*h+(c>>>30);
w[j++] = l&0x3fffffff;
}
return c;
}
// Alternately, set max digit bits to 28 since some
// browsers slow down when dealing with 32-bit numbers.
function am3(i,x,w,j,c,n) {
var xl = x&0x3fff, xh = x>>14;
while(--n >= 0) {
var l = this[i]&0x3fff;
var h = this[i++]>>14;
var m = xh*l+h*xl;
l = xl*l+((m&0x3fff)<<14)+w[j]+c;
c = (l>>28)+(m>>14)+xh*h;
w[j++] = l&0xfffffff;
}
return c;
}
if(j_lm) {
BigInteger.prototype.am = am2;
dbits = 30;
}
else if(j_lm) {
BigInteger.prototype.am = am1;
dbits = 26;
}
else { // Mozilla/Netscape seems to prefer am3
BigInteger.prototype.am = am3;
dbits = 28;
}
BigInteger.prototype.DB = dbits;
BigInteger.prototype.DM = ((1<<dbits)-1);
BigInteger.prototype.DV = (1<<dbits);
var BI_FP = 52;
BigInteger.prototype.FV = Math.pow(2,BI_FP);
BigInteger.prototype.F1 = BI_FP-dbits;
BigInteger.prototype.F2 = 2*dbits-BI_FP;
// Digit conversions
var BI_RM = "0123456789abcdefghijklmnopqrstuvwxyz";
var BI_RC = new Array();
var rr,vv;
rr = "0".charCodeAt(0);
for(vv = 0; vv <= 9; ++vv) BI_RC[rr++] = vv;
rr = "a".charCodeAt(0);
for(vv = 10; vv < 36; ++vv) BI_RC[rr++] = vv;
rr = "A".charCodeAt(0);
for(vv = 10; vv < 36; ++vv) BI_RC[rr++] = vv;
function int2char(n) { return BI_RM.charAt(n); }
function intAt(s,i) {
var c = BI_RC[s.charCodeAt(i)];
return (c==null)?-1:c;
}
// (protected) copy this to r
function bnpCopyTo(r) {
for(var i = this.t-1; i >= 0; --i) r[i] = this[i];
r.t = this.t;
r.s = this.s;
}
// (protected) set from integer value x, -DV <= x < DV
function bnpFromInt(x) {
this.t = 1;
this.s = (x<0)?-1:0;
if(x > 0) this[0] = x;
else if(x < -1) this[0] = x+DV;
else this.t = 0;
}
// return bigint initialized to value
function nbv(i) { var r = nbi(); r.fromInt(i); return r; }
// (protected) set from string and radix
function bnpFromString(s,b) {
var k;
if(b == 16) k = 4;
else if(b == 8) k = 3;
else if(b == 256) k = 8; // byte array
else if(b == 2) k = 1;
else if(b == 32) k = 5;
else if(b == 4) k = 2;
else { this.fromRadix(s,b); return; }
this.t = 0;
this.s = 0;
var i = s.length, mi = false, sh = 0;
while(--i >= 0) {
var x = (k==8)?s[i]&0xff:intAt(s,i);
if(x < 0) {
if(s.charAt(i) == "-") mi = true;
continue;
}
mi = false;
if(sh == 0)
this[this.t++] = x;
else if(sh+k > this.DB) {
this[this.t-1] |= (x&((1<<(this.DB-sh))-1))<<sh;
this[this.t++] = (x>>(this.DB-sh));
}
else
this[this.t-1] |= x<<sh;
sh += k;
if(sh >= this.DB) sh -= this.DB;
}
if(k == 8 && (s[0]&0x80) != 0) {
this.s = -1;
if(sh > 0) this[this.t-1] |= ((1<<(this.DB-sh))-1)<<sh;
}
this.clamp();
if(mi) BigInteger.ZERO.subTo(this,this);
}
// (protected) clamp off excess high words
function bnpClamp() {
var c = this.s&this.DM;
while(this.t > 0 && this[this.t-1] == c) --this.t;
}
// (public) return string representation in given radix
function bnToString(b) {
if(this.s < 0) return "-"+this.negate().toString(b);
var k;
if(b == 16) k = 4;
else if(b == 8) k = 3;
else if(b == 2) k = 1;
else if(b == 32) k = 5;
else if(b == 4) k = 2;
else return this.toRadix(b);
var km = (1<<k)-1, d, m = false, r = "", i = this.t;
var p = this.DB-(i*this.DB)%k;
if(i-- > 0) {
if(p < this.DB && (d = this[i]>>p) > 0) { m = true; r = int2char(d); }
while(i >= 0) {
if(p < k) {
d = (this[i]&((1<<p)-1))<<(k-p);
d |= this[--i]>>(p+=this.DB-k);
}
else {
d = (this[i]>>(p-=k))&km;
if(p <= 0) { p += this.DB; --i; }
}
if(d > 0) m = true;
if(m) r += int2char(d);
}
}
return m?r:"0";
}
// (public) -this
function bnNegate() { var r = nbi(); BigInteger.ZERO.subTo(this,r); return r; }
// (public) |this|
function bnAbs() { return (this.s<0)?this.negate():this; }
// (public) return + if this > a, - if this < a, 0 if equal
function bnCompareTo(a) {
var r = this.s-a.s;
if(r != 0) return r;
var i = this.t;
r = i-a.t;
if(r != 0) return r;
while(--i >= 0) if((r=this[i]-a[i]) != 0) return r;
return 0;
}
// returns bit length of the integer x
function nbits(x) {
var r = 1, t;
if((t=x>>>16) != 0) { x = t; r += 16; }
if((t=x>>8) != 0) { x = t; r += 8; }
if((t=x>>4) != 0) { x = t; r += 4; }
if((t=x>>2) != 0) { x = t; r += 2; }
if((t=x>>1) != 0) { x = t; r += 1; }
return r;
}
// (public) return the number of bits in "this"
function bnBitLength() {
if(this.t <= 0) return 0;
return this.DB*(this.t-1)+nbits(this[this.t-1]^(this.s&this.DM));
}
// (protected) r = this << n*DB
function bnpDLShiftTo(n,r) {
var i;
for(i = this.t-1; i >= 0; --i) r[i+n] = this[i];
for(i = n-1; i >= 0; --i) r[i] = 0;
r.t = this.t+n;
r.s = this.s;
}
// (protected) r = this >> n*DB
function bnpDRShiftTo(n,r) {
for(var i = n; i < this.t; ++i) r[i-n] = this[i];
r.t = Math.max(this.t-n,0);
r.s = this.s;
}
// (protected) r = this << n
function bnpLShiftTo(n,r) {
var bs = n%this.DB;
var cbs = this.DB-bs;
var bm = (1<<cbs)-1;
var ds = Math.floor(n/this.DB), c = (this.s<<bs)&this.DM, i;
for(i = this.t-1; i >= 0; --i) {
r[i+ds+1] = (this[i]>>cbs)|c;
c = (this[i]&bm)<<bs;
}
for(i = ds-1; i >= 0; --i) r[i] = 0;
r[ds] = c;
r.t = this.t+ds+1;
r.s = this.s;
r.clamp();
}
// (protected) r = this >> n
function bnpRShiftTo(n,r) {
r.s = this.s;
var ds = Math.floor(n/this.DB);
if(ds >= this.t) { r.t = 0; return; }
var bs = n%this.DB;
var cbs = this.DB-bs;
var bm = (1<<bs)-1;
r[0] = this[ds]>>bs;
for(var i = ds+1; i < this.t; ++i) {
r[i-ds-1] |= (this[i]&bm)<<cbs;
r[i-ds] = this[i]>>bs;
}
if(bs > 0) r[this.t-ds-1] |= (this.s&bm)<<cbs;
r.t = this.t-ds;
r.clamp();
}
// (protected) r = this - a
function bnpSubTo(a,r) {
var i = 0, c = 0, m = Math.min(a.t,this.t);
while(i < m) {
c += this[i]-a[i];
r[i++] = c&this.DM;
c >>= this.DB;
}
if(a.t < this.t) {
c -= a.s;
while(i < this.t) {
c += this[i];
r[i++] = c&this.DM;
c >>= this.DB;
}
c += this.s;
}
else {
c += this.s;
while(i < a.t) {
c -= a[i];
r[i++] = c&this.DM;
c >>= this.DB;
}
c -= a.s;
}
r.s = (c<0)?-1:0;
if(c < -1) r[i++] = this.DV+c;
else if(c > 0) r[i++] = c;
r.t = i;
r.clamp();
}
// (protected) r = this * a, r != this,a (HAC 14.12)
// "this" should be the larger one if appropriate.
function bnpMultiplyTo(a,r) {
var x = this.abs(), y = a.abs();
var i = x.t;
r.t = i+y.t;
while(--i >= 0) r[i] = 0;
for(i = 0; i < y.t; ++i) r[i+x.t] = x.am(0,y[i],r,i,0,x.t);
r.s = 0;
r.clamp();
if(this.s != a.s) BigInteger.ZERO.subTo(r,r);
}
// (protected) r = this^2, r != this (HAC 14.16)
function bnpSquareTo(r) {
var x = this.abs();
var i = r.t = 2*x.t;
while(--i >= 0) r[i] = 0;
for(i = 0; i < x.t-1; ++i) {
var c = x.am(i,x[i],r,2*i,0,1);
if((r[i+x.t]+=x.am(i+1,2*x[i],r,2*i+1,c,x.t-i-1)) >= x.DV) {
r[i+x.t] -= x.DV;
r[i+x.t+1] = 1;
}
}
if(r.t > 0) r[r.t-1] += x.am(i,x[i],r,2*i,0,1);
r.s = 0;
r.clamp();
}
// (protected) divide this by m, quotient and remainder to q, r (HAC 14.20)
// r != q, this != m. q or r may be null.
function bnpDivRemTo(m,q,r) {
var pm = m.abs();
if(pm.t <= 0) return;
var pt = this.abs();
if(pt.t < pm.t) {
if(q != null) q.fromInt(0);
if(r != null) this.copyTo(r);
return;
}
if(r == null) r = nbi();
var y = nbi(), ts = this.s, ms = m.s;
var nsh = this.DB-nbits(pm[pm.t-1]); // normalize modulus
if(nsh > 0) { pm.lShiftTo(nsh,y); pt.lShiftTo(nsh,r); }
else { pm.copyTo(y); pt.copyTo(r); }
var ys = y.t;
var y0 = y[ys-1];
if(y0 == 0) return;
var yt = y0*(1<<this.F1)+((ys>1)?y[ys-2]>>this.F2:0);
var d1 = this.FV/yt, d2 = (1<<this.F1)/yt, e = 1<<this.F2;
var i = r.t, j = i-ys, t = (q==null)?nbi():q;
y.dlShiftTo(j,t);
if(r.compareTo(t) >= 0) {
r[r.t++] = 1;
r.subTo(t,r);
}
BigInteger.ONE.dlShiftTo(ys,t);
t.subTo(y,y); // "negative" y so we can replace sub with am later
while(y.t < ys) y[y.t++] = 0;
while(--j >= 0) {
// Estimate quotient digit
var qd = (r[--i]==y0)?this.DM:Math.floor(r[i]*d1+(r[i-1]+e)*d2);
if((r[i]+=y.am(0,qd,r,j,0,ys)) < qd) { // Try it out
y.dlShiftTo(j,t);
r.subTo(t,r);
while(r[i] < --qd) r.subTo(t,r);
}
}
if(q != null) {
r.drShiftTo(ys,q);
if(ts != ms) BigInteger.ZERO.subTo(q,q);
}
r.t = ys;
r.clamp();
if(nsh > 0) r.rShiftTo(nsh,r); // Denormalize remainder
if(ts < 0) BigInteger.ZERO.subTo(r,r);
}
// (public) this mod a
function bnMod(a) {
var r = nbi();
this.abs().divRemTo(a,null,r);
if(this.s < 0 && r.compareTo(BigInteger.ZERO) > 0) a.subTo(r,r);
return r;
}
// Modular reduction using "classic" algorithm
function Classic(m) { this.m = m; }
function cConvert(x) {
if(x.s < 0 || x.compareTo(this.m) >= 0) return x.mod(this.m);
else return x;
}
function cRevert(x) { return x; }
function cReduce(x) { x.divRemTo(this.m,null,x); }
function cMulTo(x,y,r) { x.multiplyTo(y,r); this.reduce(r); }
function cSqrTo(x,r) { x.squareTo(r); this.reduce(r); }
Classic.prototype.convert = cConvert;
Classic.prototype.revert = cRevert;
Classic.prototype.reduce = cReduce;
Classic.prototype.mulTo = cMulTo;
Classic.prototype.sqrTo = cSqrTo;
// (protected) return "-1/this % 2^DB"; useful for Mont. reduction
// justification:
// xy == 1 (mod m)
// xy = 1+km
// xy(2-xy) = (1+km)(1-km)
// x[y(2-xy)] = 1-k^2m^2
// x[y(2-xy)] == 1 (mod m^2)
// if y is 1/x mod m, then y(2-xy) is 1/x mod m^2
// should reduce x and y(2-xy) by m^2 at each step to keep size bounded.
// JS multiply "overflows" differently from C/C++, so care is needed here.
function bnpInvDigit() {
if(this.t < 1) return 0;
var x = this[0];
if((x&1) == 0) return 0;
var y = x&3; // y == 1/x mod 2^2
y = (y*(2-(x&0xf)*y))&0xf; // y == 1/x mod 2^4
y = (y*(2-(x&0xff)*y))&0xff; // y == 1/x mod 2^8
y = (y*(2-(((x&0xffff)*y)&0xffff)))&0xffff; // y == 1/x mod 2^16
// last step - calculate inverse mod DV directly;
// assumes 16 < DB <= 32 and assumes ability to handle 48-bit ints
y = (y*(2-x*y%this.DV))%this.DV; // y == 1/x mod 2^dbits
// we really want the negative inverse, and -DV < y < DV
return (y>0)?this.DV-y:-y;
}
// Montgomery reduction
function Montgomery(m) {
this.m = m;
this.mp = m.invDigit();
this.mpl = this.mp&0x7fff;
this.mph = this.mp>>15;
this.um = (1<<(m.DB-15))-1;
this.mt2 = 2*m.t;
}
// xR mod m
function montConvert(x) {
var r = nbi();
x.abs().dlShiftTo(this.m.t,r);
r.divRemTo(this.m,null,r);
if(x.s < 0 && r.compareTo(BigInteger.ZERO) > 0) this.m.subTo(r,r);
return r;
}
// x/R mod m
function montRevert(x) {
var r = nbi();
x.copyTo(r);
this.reduce(r);
return r;
}
// x = x/R mod m (HAC 14.32)
function montReduce(x) {
while(x.t <= this.mt2) // pad x so am has enough room later
x[x.t++] = 0;
for(var i = 0; i < this.m.t; ++i) {
// faster way of calculating u0 = x[i]*mp mod DV
var j = x[i]&0x7fff;
var u0 = (j*this.mpl+(((j*this.mph+(x[i]>>15)*this.mpl)&this.um)<<15))&x.DM;
// use am to combine the multiply-shift-add into one call
j = i+this.m.t;
x[j] += this.m.am(0,u0,x,i,0,this.m.t);
// propagate carry
while(x[j] >= x.DV) { x[j] -= x.DV; x[++j]++; }
}
x.clamp();
x.drShiftTo(this.m.t,x);
if(x.compareTo(this.m) >= 0) x.subTo(this.m,x);
}
// r = "x^2/R mod m"; x != r
function montSqrTo(x,r) { x.squareTo(r); this.reduce(r); }
// r = "xy/R mod m"; x,y != r
function montMulTo(x,y,r) { x.multiplyTo(y,r); this.reduce(r); }
Montgomery.prototype.convert = montConvert;
Montgomery.prototype.revert = montRevert;
Montgomery.prototype.reduce = montReduce;
Montgomery.prototype.mulTo = montMulTo;
Montgomery.prototype.sqrTo = montSqrTo;
// (protected) true iff this is even
function bnpIsEven() { return ((this.t>0)?(this[0]&1):this.s) == 0; }
// (protected) this^e, e < 2^32, doing sqr and mul with "r" (HAC 14.79)
function bnpExp(e,z) {
if(e > 0xffffffff || e < 1) return BigInteger.ONE;
var r = nbi(), r2 = nbi(), g = z.convert(this), i = nbits(e)-1;
g.copyTo(r);
while(--i >= 0) {
z.sqrTo(r,r2);
if((e&(1<<i)) > 0) z.mulTo(r2,g,r);
else { var t = r; r = r2; r2 = t; }
}
return z.revert(r);
}
// (public) this^e % m, 0 <= e < 2^32
function bnModPowInt(e,m) {
var z;
if(e < 256 || m.isEven()) z = new Classic(m); else z = new Montgomery(m);
return this.exp(e,z);
}
// protected
BigInteger.prototype.copyTo = bnpCopyTo;
BigInteger.prototype.fromInt = bnpFromInt;
BigInteger.prototype.fromString = bnpFromString;
BigInteger.prototype.clamp = bnpClamp;
BigInteger.prototype.dlShiftTo = bnpDLShiftTo;
BigInteger.prototype.drShiftTo = bnpDRShiftTo;
BigInteger.prototype.lShiftTo = bnpLShiftTo;
BigInteger.prototype.rShiftTo = bnpRShiftTo;
BigInteger.prototype.subTo = bnpSubTo;
BigInteger.prototype.multiplyTo = bnpMultiplyTo;
BigInteger.prototype.squareTo = bnpSquareTo;
BigInteger.prototype.divRemTo = bnpDivRemTo;
BigInteger.prototype.invDigit = bnpInvDigit;
BigInteger.prototype.isEven = bnpIsEven;
BigInteger.prototype.exp = bnpExp;
// public
BigInteger.prototype.toString = bnToString;
BigInteger.prototype.negate = bnNegate;
BigInteger.prototype.abs = bnAbs;
BigInteger.prototype.compareTo = bnCompareTo;
BigInteger.prototype.bitLength = bnBitLength;
BigInteger.prototype.mod = bnMod;
BigInteger.prototype.modPowInt = bnModPowInt;
// "constants"
BigInteger.ZERO = nbv(0);
BigInteger.ONE = nbv(1);
// Copyright (c) 2005 Tom Wu
// All Rights Reserved.
// See "LICENSE" for details.
// Extended JavaScript BN functions, required for RSA private ops.
// (public)
function bnClone() { var r = nbi(); this.copyTo(r); return r; }
// (public) return value as integer
function bnIntValue() {
if(this.s < 0) {
if(this.t == 1) return this[0]-this.DV;
else if(this.t == 0) return -1;
}
else if(this.t == 1) return this[0];
else if(this.t == 0) return 0;
// assumes 16 < DB < 32
return ((this[1]&((1<<(32-this.DB))-1))<<this.DB)|this[0];
}
// (public) return value as byte
function bnByteValue() { return (this.t==0)?this.s:(this[0]<<24)>>24; }
// (public) return value as short (assumes DB>=16)
function bnShortValue() { return (this.t==0)?this.s:(this[0]<<16)>>16; }
// (protected) return x s.t. r^x < DV
function bnpChunkSize(r) { return Math.floor(Math.LN2*this.DB/Math.log(r)); }
// (public) 0 if this == 0, 1 if this > 0
function bnSigNum() {
if(this.s < 0) return -1;
else if(this.t <= 0 || (this.t == 1 && this[0] <= 0)) return 0;
else return 1;
}
// (protected) convert to radix string
function bnpToRadix(b) {
if(b == null) b = 10;
if(this.signum() == 0 || b < 2 || b > 36) return "0";
var cs = this.chunkSize(b);
var a = Math.pow(b,cs);
var d = nbv(a), y = nbi(), z = nbi(), r = "";
this.divRemTo(d,y,z);
while(y.signum() > 0) {
r = (a+z.intValue()).toString(b).substr(1) + r;
y.divRemTo(d,y,z);
}
return z.intValue().toString(b) + r;
}
// (protected) convert from radix string
function bnpFromRadix(s,b) {
this.fromInt(0);
if(b == null) b = 10;
var cs = this.chunkSize(b);
var d = Math.pow(b,cs), mi = false, j = 0, w = 0;
for(var i = 0; i < s.length; ++i) {
var x = intAt(s,i);
if(x < 0) {
if(s.charAt(i) == "-" && this.signum() == 0) mi = true;
continue;
}
w = b*w+x;
if(++j >= cs) {
this.dMultiply(d);
this.dAddOffset(w,0);
j = 0;
w = 0;
}
}
if(j > 0) {
this.dMultiply(Math.pow(b,j));
this.dAddOffset(w,0);
}
if(mi) BigInteger.ZERO.subTo(this,this);
}
// (protected) alternate constructor
function bnpFromNumber(a,b,c) {
if("number" == typeof b) {
// new BigInteger(int,int,RNG)
if(a < 2) this.fromInt(1);
else {
this.fromNumber(a,c);
if(!this.testBit(a-1)) // force MSB set
this.bitwiseTo(BigInteger.ONE.shiftLeft(a-1),op_or,this);
if(this.isEven()) this.dAddOffset(1,0); // force odd
while(!this.isProbablePrime(b)) {
this.dAddOffset(2,0);
if(this.bitLength() > a) this.subTo(BigInteger.ONE.shiftLeft(a-1),this);
}
}
}
else {
// new BigInteger(int,RNG)
var x = new Array(), t = a&7;
x.length = (a>>3)+1;
b.nextBytes(x);
if(t > 0) x[0] &= ((1<<t)-1); else x[0] = 0;
this.fromString(x,256);
}
}
// (public) convert to bigendian byte array
function bnToByteArray() {
var i = this.t, r = new Array();
r[0] = this.s;
var p = this.DB-(i*this.DB)%8, d, k = 0;
if(i-- > 0) {
if(p < this.DB && (d = this[i]>>p) != (this.s&this.DM)>>p)
r[k++] = d|(this.s<<(this.DB-p));
while(i >= 0) {
if(p < 8) {
d = (this[i]&((1<<p)-1))<<(8-p);
d |= this[--i]>>(p+=this.DB-8);
}
else {
d = (this[i]>>(p-=8))&0xff;
if(p <= 0) { p += this.DB; --i; }
}
if((d&0x80) != 0) d |= -256;
if(k == 0 && (this.s&0x80) != (d&0x80)) ++k;
if(k > 0 || d != this.s) r[k++] = d;
}
}
return r;
}
function bnEquals(a) { return(this.compareTo(a)==0); }
function bnMin(a) { return(this.compareTo(a)<0)?this:a; }
function bnMax(a) { return(this.compareTo(a)>0)?this:a; }
// (protected) r = this op a (bitwise)
function bnpBitwiseTo(a,op,r) {
var i, f, m = Math.min(a.t,this.t);
for(i = 0; i < m; ++i) r[i] = op(this[i],a[i]);
if(a.t < this.t) {
f = a.s&this.DM;
for(i = m; i < this.t; ++i) r[i] = op(this[i],f);
r.t = this.t;
}
else {
f = this.s&this.DM;
for(i = m; i < a.t; ++i) r[i] = op(f,a[i]);
r.t = a.t;
}
r.s = op(this.s,a.s);
r.clamp();
}
// (public) this & a
function op_and(x,y) { return x&y; }
function bnAnd(a) { var r = nbi(); this.bitwiseTo(a,op_and,r); return r; }
// (public) this | a
function op_or(x,y) { return x|y; }
function bnOr(a) { var r = nbi(); this.bitwiseTo(a,op_or,r); return r; }
// (public) this ^ a
function op_xor(x,y) { return x^y; }
function bnXor(a) { var r = nbi(); this.bitwiseTo(a,op_xor,r); return r; }
// (public) this & ~a
function op_andnot(x,y) { return x&~y; }
function bnAndNot(a) { var r = nbi(); this.bitwiseTo(a,op_andnot,r); return r; }
// (public) ~this
function bnNot() {
var r = nbi();
for(var i = 0; i < this.t; ++i) r[i] = this.DM&~this[i];
r.t = this.t;
r.s = ~this.s;
return r;
}
// (public) this << n
function bnShiftLeft(n) {
var r = nbi();
if(n < 0) this.rShiftTo(-n,r); else this.lShiftTo(n,r);
return r;
}
// (public) this >> n
function bnShiftRight(n) {
var r = nbi();
if(n < 0) this.lShiftTo(-n,r); else this.rShiftTo(n,r);
return r;
}
// return index of lowest 1-bit in x, x < 2^31
function lbit(x) {
if(x == 0) return -1;
var r = 0;
if((x&0xffff) == 0) { x >>= 16; r += 16; }
if((x&0xff) == 0) { x >>= 8; r += 8; }
if((x&0xf) == 0) { x >>= 4; r += 4; }
if((x&3) == 0) { x >>= 2; r += 2; }
if((x&1) == 0) ++r;
return r;
}
// (public) returns index of lowest 1-bit (or -1 if none)
function bnGetLowestSetBit() {
for(var i = 0; i < this.t; ++i)
if(this[i] != 0) return i*this.DB+lbit(this[i]);
if(this.s < 0) return this.t*this.DB;
return -1;
}
// return number of 1 bits in x
function cbit(x) {
var r = 0;
while(x != 0) { x &= x-1; ++r; }
return r;
}
// (public) return number of set bits
function bnBitCount() {
var r = 0, x = this.s&this.DM;
for(var i = 0; i < this.t; ++i) r += cbit(this[i]^x);
return r;
}
// (public) true iff nth bit is set
function bnTestBit(n) {
var j = Math.floor(n/this.DB);
if(j >= this.t) return(this.s!=0);
return((this[j]&(1<<(n%this.DB)))!=0);
}
// (protected) this op (1<<n)
function bnpChangeBit(n,op) {
var r = BigInteger.ONE.shiftLeft(n);
this.bitwiseTo(r,op,r);
return r;
}
// (public) this | (1<<n)
function bnSetBit(n) { return this.changeBit(n,op_or); }
// (public) this & ~(1<<n)
function bnClearBit(n) { return this.changeBit(n,op_andnot); }
// (public) this ^ (1<<n)
function bnFlipBit(n) { return this.changeBit(n,op_xor); }
// (protected) r = this + a
function bnpAddTo(a,r) {
var i = 0, c = 0, m = Math.min(a.t,this.t);
while(i < m) {
c += this[i]+a[i];
r[i++] = c&this.DM;
c >>= this.DB;
}
if(a.t < this.t) {
c += a.s;
while(i < this.t) {
c += this[i];
r[i++] = c&this.DM;
c >>= this.DB;
}
c += this.s;
}
else {
c += this.s;
while(i < a.t) {
c += a[i];
r[i++] = c&this.DM;
c >>= this.DB;
}
c += a.s;
}
r.s = (c<0)?-1:0;
if(c > 0) r[i++] = c;
else if(c < -1) r[i++] = this.DV+c;
r.t = i;
r.clamp();
}
// (public) this + a
function bnAdd(a) { var r = nbi(); this.addTo(a,r); return r; }
// (public) this - a
function bnSubtract(a) { var r = nbi(); this.subTo(a,r); return r; }
// (public) this * a
function bnMultiply(a) { var r = nbi(); this.multiplyTo(a,r); return r; }
// (public) this / a
function bnDivide(a) { var r = nbi(); this.divRemTo(a,r,null); return r; }
// (public) this % a
function bnRemainder(a) { var r = nbi(); this.divRemTo(a,null,r); return r; }
// (public) [this/a,this%a]
function bnDivideAndRemainder(a) {
var q = nbi(), r = nbi();
this.divRemTo(a,q,r);
return new Array(q,r);
}
// (protected) this *= n, this >= 0, 1 < n < DV
function bnpDMultiply(n) {
this[this.t] = this.am(0,n-1,this,0,0,this.t);
++this.t;
this.clamp();
}
// (protected) this += n << w words, this >= 0
function bnpDAddOffset(n,w) {
while(this.t <= w) this[this.t++] = 0;
this[w] += n;
while(this[w] >= this.DV) {
this[w] -= this.DV;
if(++w >= this.t) this[this.t++] = 0;
++this[w];
}
}
// A "null" reducer
function NullExp() {}
function nNop(x) { return x; }
function nMulTo(x,y,r) { x.multiplyTo(y,r); }
function nSqrTo(x,r) { x.squareTo(r); }
NullExp.prototype.convert = nNop;
NullExp.prototype.revert = nNop;
NullExp.prototype.mulTo = nMulTo;
NullExp.prototype.sqrTo = nSqrTo;
// (public) this^e
function bnPow(e) { return this.exp(e,new NullExp()); }
// (protected) r = lower n words of "this * a", a.t <= n
// "this" should be the larger one if appropriate.
function bnpMultiplyLowerTo(a,n,r) {
var i = Math.min(this.t+a.t,n);
r.s = 0; // assumes a,this >= 0
r.t = i;
while(i > 0) r[--i] = 0;
var j;
for(j = r.t-this.t; i < j; ++i) r[i+this.t] = this.am(0,a[i],r,i,0,this.t);
for(j = Math.min(a.t,n); i < j; ++i) this.am(0,a[i],r,i,0,n-i);
r.clamp();
}
// (protected) r = "this * a" without lower n words, n > 0
// "this" should be the larger one if appropriate.
function bnpMultiplyUpperTo(a,n,r) {
--n;
var i = r.t = this.t+a.t-n;
r.s = 0; // assumes a,this >= 0
while(--i >= 0) r[i] = 0;
for(i = Math.max(n-this.t,0); i < a.t; ++i)
r[this.t+i-n] = this.am(n-i,a[i],r,0,0,this.t+i-n);
r.clamp();
r.drShiftTo(1,r);
}
// Barrett modular reduction
function Barrett(m) {
// setup Barrett
this.r2 = nbi();
this.q3 = nbi();
BigInteger.ONE.dlShiftTo(2*m.t,this.r2);
this.mu = this.r2.divide(m);
this.m = m;
}
function barrettConvert(x) {
if(x.s < 0 || x.t > 2*this.m.t) return x.mod(this.m);
else if(x.compareTo(this.m) < 0) return x;
else { var r = nbi(); x.copyTo(r); this.reduce(r); return r; }
}
function barrettRevert(x) { return x; }
// x = x mod m (HAC 14.42)
function barrettReduce(x) {
x.drShiftTo(this.m.t-1,this.r2);
if(x.t > this.m.t+1) { x.t = this.m.t+1; x.clamp(); }
this.mu.multiplyUpperTo(this.r2,this.m.t+1,this.q3);
this.m.multiplyLowerTo(this.q3,this.m.t+1,this.r2);
while(x.compareTo(this.r2) < 0) x.dAddOffset(1,this.m.t+1);
x.subTo(this.r2,x);
while(x.compareTo(this.m) >= 0) x.subTo(this.m,x);
}
// r = x^2 mod m; x != r
function barrettSqrTo(x,r) { x.squareTo(r); this.reduce(r); }
// r = x*y mod m; x,y != r
function barrettMulTo(x,y,r) { x.multiplyTo(y,r); this.reduce(r); }
Barrett.prototype.convert = barrettConvert;
Barrett.prototype.revert = barrettRevert;
Barrett.prototype.reduce = barrettReduce;
Barrett.prototype.mulTo = barrettMulTo;
Barrett.prototype.sqrTo = barrettSqrTo;
// (public) this^e % m (HAC 14.85)
function bnModPow(e,m) {
var i = e.bitLength(), k, r = nbv(1), z;
if(i <= 0) return r;
else if(i < 18) k = 1;
else if(i < 48) k = 3;
else if(i < 144) k = 4;
else if(i < 768) k = 5;
else k = 6;
if(i < 8)
z = new Classic(m);
else if(m.isEven())
z = new Barrett(m);
else
z = new Montgomery(m);
// precomputation
var g = new Array(), n = 3, k1 = k-1, km = (1<<k)-1;
g[1] = z.convert(this);
if(k > 1) {
var g2 = nbi();
z.sqrTo(g[1],g2);
while(n <= km) {
g[n] = nbi();
z.mulTo(g2,g[n-2],g[n]);
n += 2;
}
}
var j = e.t-1, w, is1 = true, r2 = nbi(), t;
i = nbits(e[j])-1;
while(j >= 0) {
if(i >= k1) w = (e[j]>>(i-k1))&km;
else {
w = (e[j]&((1<<(i+1))-1))<<(k1-i);
if(j > 0) w |= e[j-1]>>(this.DB+i-k1);
}
n = k;
while((w&1) == 0) { w >>= 1; --n; }
if((i -= n) < 0) { i += this.DB; --j; }
if(is1) { // ret == 1, don't bother squaring or multiplying it
g[w].copyTo(r);
is1 = false;
}
else {
while(n > 1) { z.sqrTo(r,r2); z.sqrTo(r2,r); n -= 2; }
if(n > 0) z.sqrTo(r,r2); else { t = r; r = r2; r2 = t; }
z.mulTo(r2,g[w],r);
}
while(j >= 0 && (e[j]&(1<<i)) == 0) {
z.sqrTo(r,r2); t = r; r = r2; r2 = t;
if(--i < 0) { i = this.DB-1; --j; }
}
}
return z.revert(r);
}
// (public) gcd(this,a) (HAC 14.54)
function bnGCD(a) {
var x = (this.s<0)?this.negate():this.clone();
var y = (a.s<0)?a.negate():a.clone();
if(x.compareTo(y) < 0) { var t = x; x = y; y = t; }
var i = x.getLowestSetBit(), g = y.getLowestSetBit();
if(g < 0) return x;
if(i < g) g = i;
if(g > 0) {
x.rShiftTo(g,x);
y.rShiftTo(g,y);
}
while(x.signum() > 0) {
if((i = x.getLowestSetBit()) > 0) x.rShiftTo(i,x);
if((i = y.getLowestSetBit()) > 0) y.rShiftTo(i,y);
if(x.compareTo(y) >= 0) {
x.subTo(y,x);
x.rShiftTo(1,x);
}
else {
y.subTo(x,y);
y.rShiftTo(1,y);
}
}
if(g > 0) y.lShiftTo(g,y);
return y;
}
// (protected) this % n, n < 2^26
function bnpModInt(n) {
if(n <= 0) return 0;
var d = this.DV%n, r = (this.s<0)?n-1:0;
if(this.t > 0)
if(d == 0) r = this[0]%n;
else for(var i = this.t-1; i >= 0; --i) r = (d*r+this[i])%n;
return r;
}
// (public) 1/this % m (HAC 14.61)
function bnModInverse(m) {
var ac = m.isEven();
if((this.isEven() && ac) || m.signum() == 0) return BigInteger.ZERO;
var u = m.clone(), v = this.clone();
var a = nbv(1), b = nbv(0), c = nbv(0), d = nbv(1);
while(u.signum() != 0) {
while(u.isEven()) {
u.rShiftTo(1,u);
if(ac) {
if(!a.isEven() || !b.isEven()) { a.addTo(this,a); b.subTo(m,b); }
a.rShiftTo(1,a);
}
else if(!b.isEven()) b.subTo(m,b);
b.rShiftTo(1,b);
}
while(v.isEven()) {
v.rShiftTo(1,v);
if(ac) {
if(!c.isEven() || !d.isEven()) { c.addTo(this,c); d.subTo(m,d); }
c.rShiftTo(1,c);
}
else if(!d.isEven()) d.subTo(m,d);
d.rShiftTo(1,d);
}
if(u.compareTo(v) >= 0) {
u.subTo(v,u);
if(ac) a.subTo(c,a);
b.subTo(d,b);
}
else {
v.subTo(u,v);
if(ac) c.subTo(a,c);
d.subTo(b,d);
}
}
if(v.compareTo(BigInteger.ONE) != 0) return BigInteger.ZERO;
if(d.compareTo(m) >= 0) return d.subtract(m);
if(d.signum() < 0) d.addTo(m,d); else return d;
if(d.signum() < 0) return d.add(m); else return d;
}
var lowprimes = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,349,353,359,367,373,379,383,389,397,401,409,419,421,431,433,439,443,449,457,461,463,467,479,487,491,499,503,509];
var lplim = (1<<26)/lowprimes[lowprimes.length-1];
// (public) test primality with certainty >= 1-.5^t
function bnIsProbablePrime(t) {
var i, x = this.abs();
if(x.t == 1 && x[0] <= lowprimes[lowprimes.length-1]) {
for(i = 0; i < lowprimes.length; ++i)
if(x[0] == lowprimes[i]) return true;
return false;
}
if(x.isEven()) return false;
i = 1;
while(i < lowprimes.length) {
var m = lowprimes[i], j = i+1;
while(j < lowprimes.length && m < lplim) m *= lowprimes[j++];
m = x.modInt(m);
while(i < j) if(m%lowprimes[i++] == 0) return false;
}
return x.millerRabin(t);
}
// (protected) true if probably prime (HAC 4.24, Miller-Rabin)
function bnpMillerRabin(t) {
var n1 = this.subtract(BigInteger.ONE);
var k = n1.getLowestSetBit();
if(k <= 0) return false;
var r = n1.shiftRight(k);
t = (t+1)>>1;
if(t > lowprimes.length) t = lowprimes.length;
var a = nbi();
for(var i = 0; i < t; ++i) {
a.fromInt(lowprimes[i]);
var y = a.modPow(r,this);
if(y.compareTo(BigInteger.ONE) != 0 && y.compareTo(n1) != 0) {
var j = 1;
while(j++ < k && y.compareTo(n1) != 0) {
y = y.modPowInt(2,this);
if(y.compareTo(BigInteger.ONE) == 0) return false;
}
if(y.compareTo(n1) != 0) return false;
}
}
return true;
}
// protected
BigInteger.prototype.chunkSize = bnpChunkSize;
BigInteger.prototype.toRadix = bnpToRadix;
BigInteger.prototype.fromRadix = bnpFromRadix;
BigInteger.prototype.fromNumber = bnpFromNumber;
BigInteger.prototype.bitwiseTo = bnpBitwiseTo;
BigInteger.prototype.changeBit = bnpChangeBit;
BigInteger.prototype.addTo = bnpAddTo;
BigInteger.prototype.dMultiply = bnpDMultiply;
BigInteger.prototype.dAddOffset = bnpDAddOffset;
BigInteger.prototype.multiplyLowerTo = bnpMultiplyLowerTo;
BigInteger.prototype.multiplyUpperTo = bnpMultiplyUpperTo;
BigInteger.prototype.modInt = bnpModInt;
BigInteger.prototype.millerRabin = bnpMillerRabin;
// public
BigInteger.prototype.clone = bnClone;
BigInteger.prototype.intValue = bnIntValue;
BigInteger.prototype.byteValue = bnByteValue;
BigInteger.prototype.shortValue = bnShortValue;
BigInteger.prototype.signum = bnSigNum;
BigInteger.prototype.toByteArray = bnToByteArray;
BigInteger.prototype.equals = bnEquals;
BigInteger.prototype.min = bnMin;
BigInteger.prototype.max = bnMax;
BigInteger.prototype.and = bnAnd;
BigInteger.prototype.or = bnOr;
BigInteger.prototype.xor = bnXor;
BigInteger.prototype.andNot = bnAndNot;
BigInteger.prototype.not = bnNot;
BigInteger.prototype.shiftLeft = bnShiftLeft;
BigInteger.prototype.shiftRight = bnShiftRight;
BigInteger.prototype.getLowestSetBit = bnGetLowestSetBit;
BigInteger.prototype.bitCount = bnBitCount;
BigInteger.prototype.testBit = bnTestBit;
BigInteger.prototype.setBit = bnSetBit;
BigInteger.prototype.clearBit = bnClearBit;
BigInteger.prototype.flipBit = bnFlipBit;
BigInteger.prototype.add = bnAdd;
BigInteger.prototype.subtract = bnSubtract;
BigInteger.prototype.multiply = bnMultiply;
BigInteger.prototype.divide = bnDivide;
BigInteger.prototype.remainder = bnRemainder;
BigInteger.prototype.divideAndRemainder = bnDivideAndRemainder;
BigInteger.prototype.modPow = bnModPow;
BigInteger.prototype.modInverse = bnModInverse;
BigInteger.prototype.pow = bnPow;
BigInteger.prototype.gcd = bnGCD;
BigInteger.prototype.isProbablePrime = bnIsProbablePrime;
// BigInteger interfaces not implemented in jsbn:
// BigInteger(int signum, byte[] magnitude)
// double doubleValue()
// float floatValue()
// int hashCode()
// long longValue()
// static BigInteger valueOf(long val)
var RSAPublicKey = function($modulus_hex, $encryptionExponent_hex) {
this.modulus = new BigInteger( $modulus_hex, 16);
this.encryptionExponent = new BigInteger( $encryptionExponent_hex, 16);
};
var Base64 = {
base64: "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/=",
encode: function($input) {
if (!$input) {
return false;
}
var $output = "";
var $chr1, $chr2, $chr3;
var $enc1, $enc2, $enc3, $enc4;
var $i = 0;
do {
$chr1 = $input.charCodeAt($i++);
$chr2 = $input.charCodeAt($i++);
$chr3 = $input.charCodeAt($i++);
$enc1 = $chr1 >> 2;
$enc2 = (($chr1 & 3) << 4) | ($chr2 >> 4);
$enc3 = (($chr2 & 15) << 2) | ($chr3 >> 6);
$enc4 = $chr3 & 63;
if (isNaN($chr2)) $enc3 = $enc4 = 64;
else if (isNaN($chr3)) $enc4 = 64;
$output += this.base64.charAt($enc1) + this.base64.charAt($enc2) + this.base64.charAt($enc3) + this.base64.charAt($enc4);
} while ($i < $input.length);
return $output;
},
decode: function($input) {
if(!$input) return false;
$input = $input.replace(/[^A-Za-z0-9\+\/\=]/g, "");
var $output = "";
var $enc1, $enc2, $enc3, $enc4;
var $i = 0;
do {
$enc1 = this.base64.indexOf($input.charAt($i++));
$enc2 = this.base64.indexOf($input.charAt($i++));
$enc3 = this.base64.indexOf($input.charAt($i++));
$enc4 = this.base64.indexOf($input.charAt($i++));
$output += String.fromCharCode(($enc1 << 2) | ($enc2 >> 4));
if ($enc3 != 64) $output += String.fromCharCode((($enc2 & 15) << 4) | ($enc3 >> 2));
if ($enc4 != 64) $output += String.fromCharCode((($enc3 & 3) << 6) | $enc4);
} while ($i < $input.length);
return $output;
}
};
var Hex = {
hex: "0123456789abcdef",
encode: function($input) {
if(!$input) return false;
var $output = "";
var $k;
var $i = 0;
do {
$k = $input.charCodeAt($i++);
$output += this.hex.charAt(($k >> 4) &0xf) + this.hex.charAt($k & 0xf);
} while ($i < $input.length);
return $output;
},
decode: function($input) {
if(!$input) return false;
$input = $input.replace(/[^0-9abcdef]/g, "");
var $output = "";
var $i = 0;
do {
$output += String.fromCharCode(((this.hex.indexOf($input.charAt($i++)) << 4) & 0xf0) | (this.hex.indexOf($input.charAt($i++)) & 0xf));
} while ($i < $input.length);
return $output;
}
};
var RSA = {
getPublicKey: function( $modulus_hex, $exponent_hex ) {
return new RSAPublicKey( $modulus_hex, $exponent_hex );
},
encrypt: function($data, $pubkey) {
if (!$pubkey) return false;
$data = this.pkcs1pad2($data,($pubkey.modulus.bitLength()+7)>>3);
if(!$data) return false;
$data = $data.modPowInt($pubkey.encryptionExponent, $pubkey.modulus);
if(!$data) return false;
$data = $data.toString(16);
if(($data.length & 1) == 1)
$data = "0" + $data;
return Base64.encode(Hex.decode($data));
},
pkcs1pad2: function($data, $keysize) {
if($keysize < $data.length + 11)
return null;
var $buffer = [];
var $i = $data.length - 1;
while($i >= 0 && $keysize > 0)
$buffer[--$keysize] = $data.charCodeAt($i--);
$buffer[--$keysize] = 0;
while($keysize > 2)
$buffer[--$keysize] = Math.floor(Math.random()*254) + 1;
$buffer[--$keysize] = 2;
$buffer[--$keysize] = 0;
return new BigInteger($buffer);
}
};
OnAuthCodeResponse = function(results, password) {
// var form = this.m_$LogonForm[0];
var pubKey = RSA.getPublicKey(results.publickey_mod, results.publickey_exp);
// var username = this.m_strUsernameCanonical;
// var password = form.elements['password'].value;
password = password.replace(/[^\x00-\x7F]/g, '');
// remove non-standard-ASCII characters
var encryptedPassword = RSA.encrypt(password, pubKey);
return encryptedPassword
};
console.log(OnAuthCodeResponse({'success': 'True', 'publickey_mod': 'aef25caaaba051405eb6be0ee34e927aa7378248279345a5c9cdb4f873de605e81167608b3f8592b7692d592373dae0b3b8e878dbcb3c25dda0d83d8b0b5e5432e59d33210749537f596841b7bd989594e6109d2ab63aed23052b0667de72c22e64f2e09a55066bf861bcf24f79336e75caff55887409c695bdf232d846b9e73a89a2df20a28fb580a504188f4a9e16e759e7aa5f454ce6e03aebf998cbc6ed478c24069af6ee8e06954fb9748bc387d811bfb33bc8d00b5400134bcbb8e872be4e8e60924754c10c522539dd1feeebc71f36c3f1d0484a914b8cbfb9966b403923d98821f02de5ec5d3ffba0b022dbf7cbfcec3fb88278bee580fe8f40960f9', 'publickey_exp': '010001', 'timestamp': '133267600000', 'token_gid': '27ddf868c7def6b4'}, '12345'))
// Gq8LwJWnpwJS438pSVx7qnOW0gGGAv7gZbZKmbQtVcww4wVqck0FPUYScf8IyBz7DIbNawHVrx4lShLCS2oOPqxKNV6IybKESkARGXV4TqiVHF36oXejbO89zFWop5JDBeZl1nbV2y99fbSqAx2P/oxt3lm33xebkwc42KJqK1sAHK+dZ8YVT1Ji9J3JNeTVZvoH/4I5oRkb2ai5DsURllQkGvut3b9eGx6MSumCTp0YCVGjE4oE9WSq8Gvq7sD7F8QNobfRGUKk1TvcYmeqwDtSTGQWascbAic7+/yKV0ej2AyHyIQ/nnUMWjI4HWDRAqxyAHKkB6mPFLKKJZiQLQ==
簡易源碼分享
import time
import execjs
import requests
login_url = 'https://store.steampowered.com/login/dologin/'
get_rsa_key_url = 'https://store.steampowered.com/login/getrsakey/'
headers = {
'Host': 'store.steampowered.com',
'Origin': 'https://store.steampowered.com',
'Referer': 'https://store.steampowered.com/login/?redir=&redir_ssl=1&snr=1_4_4__global-header',
'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/91.0.4472.124 Safari/537.36Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/94.0.4606.71 Safari/537.36'
}
session = requests.session()
def get_rsa_key(username):
data = {
'donotcache': str(int(time.time() * 1000)),
'username': username
}
response = session.post(url=get_rsa_key_url, data=data, headers=headers).json()
print(response)
return response
def get_encrypted_password(password, rsa_key_dict):
f = open('steam.js', 'r', encoding='utf-8')
steampowered_js = f.read()
f.close()
encrypted_password = execjs.compile(steampowered_js).call('OnAuthCodeResponse', password, rsa_key_dict)
return encrypted_password
def login(username, encrypted_password, rsa_key_dict):
data = {
'donotcache': str(int(time.time() * 1000)),
'password': encrypted_password,
'username': username,
'twofactorcode': '',
'emailauth': '',
'loginfriendlyname': '',
'emailsteamid': '',
'rsatimestamp': rsa_key_dict['timestamp'],
'remember_login': False,
'tokentype': '-1'
}
print(data)
response = session.post(url=login_url, data=data, headers=headers)
print(response.text)
def main():
username = input('請輸入登錄賬號: ')
password = input('請輸入登錄密碼: ')
# 獲取 RSA 加密所需 key 等信息
rsa_key_dict = get_rsa_key(username)
# 獲取加密後的密碼
encrypted_password = get_encrypted_password(password, rsa_key_dict)
# print(encrypted_password)
# 攜帶 用戶名、加密後的密碼、cookies、驗證碼等登錄
login(username, encrypted_password, rsa_key_dict)
if __name__ == '__main__':
main()
以上就是python爬蟲實戰steam加密逆向RSA登錄解析的詳細內容,更多關於爬蟲steam加密逆向RSA登錄的資料請關註WalkonNet其它相關文章!
推薦閱讀:
- Python幹貨實戰之逆向登錄世界上最大的遊戲平臺Stream
- C++實現LeetCode(91.解碼方法)
- C++實現LeetCode(14.最長共同前綴)
- Java Big Number操作BigInteger及BigDecimal類詳解
- Java 處理超大數類型之BigInteger案例詳解