python光學仿真實現光線追跡折射與反射的實現

Posted on by

折射與反射

光線與光學元件相互作用，無非隻有兩件事，反射和透射。而就目前看來，我們所常用的光學元件，也無非有兩種表面，即平面和球面，二維化之後就簡化成瞭射線與線段，射線與劣弧的關系。

平面反射

無論從哪個角度來看，平面的反射折射都要比球面更簡單，而反射問題要比折射問題更簡單，所以，我們首先處理平面的反射問題。

反射定律即入射角等於反射角，心念及此，最為循規蹈矩的思路必然是先找到入射光線和平面的夾角，然後用這個夾角和平面(在二維空間中是一條直線)在空間中的斜率，由這個斜率與入射角得到出射光的斜率，然後就可以得到出射光的方程。

這個方法的問題是需要反復使用三角函數和反三角函數，而三角函數和反三角函數並非嚴格意義上的互為相反，所以在傳參的過程中，可能會遇到一些麻煩。

相對來說，比較不容易出錯的方法是，尋找入射點關於法線的對稱點，那麼這個對稱點與交點的連線，便是出射光的方程。

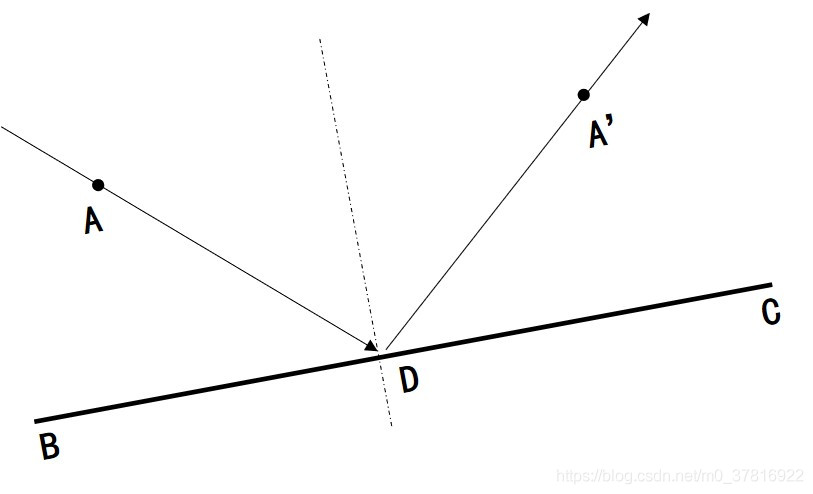
在這裡插入圖片描述

在這裡插入圖片描述

平面折射

折射與反射的思路如出一轍，最原始的想法仍舊是獲取入射角，然後根據折射定律求出射角，然後再按照出射角解出出射光的表達式。這個思路的難點仍舊在三角函數與反函數的轉化上。

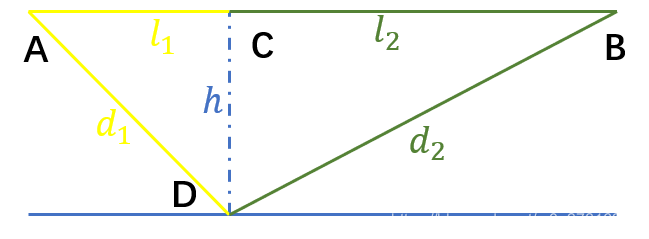
在這裡插入圖片描述

在這裡插入圖片描述

在這裡插入圖片描述

至此，我們發現折射與反射在表達形式上是相通的，如果令入射點關於法線做垂線，垂足為C，約定這條垂線與出射光線的交點為出射點B，那麼出射點到垂足的距離BC與入射點到垂足的距離AC之間是滿足比例關系的。當入射光線和反射光線的折射率相等時，這個比例為1，否則比例為 λ \lambda λ。

我們還能發現，這個 λ \lambda λ不一定有解，因為分母中有一個根號表達式，當內部的值小於0時，自然無解。這與我們的物理直覺是符合的，即並不是所有的入射光線都有折射光線，當折射光線消失的時候，就發生瞭全反射。

所以，當務之急是根據入射點找垂足，易得

在這裡插入圖片描述

那麼對於我們所熟知的折射問題，即可令入射點關於反射平面做一次對稱，再關於發現做一次定比延長線的對稱，即可得到出射點。

python實現

至此，我們已經完全建立瞭一套反射與折射的關系，代碼如下：

#得到點關於直線的對稱點,k為比例系數
def getSymDot(point,line,k=1):
    return tuple((np.array(getPedal(point,line))*(1+k)-point)/k)
#得到直線的垂足
def getPedal(point,line):
    a,b,c=line
    x0,y0 = point
    y1 = (a**2*y0-a*b*x0-b*c)/(a**2+b**2)
    x1 = (b**2*x0-a*b*y0-a*c)/(a**2+b**2)
    return (x1,y1)

函數getSymDot即通過輸入點和線來求解對稱點，其思路是把點關於線對稱的問題轉化為點關於垂足對稱的問題。所以引用瞭getPedal函數，這個函數通過輸入一點和線來返回過點做線的垂線所得到的垂足。

所有代碼都是對上述數學公式的簡單復現。

def cataDioLine(abc=[1,-1,1],line=[2,-1,1],
                sPoint=[],cross=[],n1=1,n2=1.5):
    normal = [-line[1],line[0],line[1]*cross[0]-line[0]*cross[1]]#法線
    flecDot = getSymDot(sPoint,normal)
    flec=getABC([cross,flecDot])
    dPara = np.sqrt(line[0]**2+line[1]**2)
    dNormal = np.abs(np.array(normal).dot(list(sPoint)+[1]))/dPara#到法線距離
    dPane = np.abs(np.array(line).dot(list(sPoint)+[1]))/dPara#到反射面距離
    if dNormal == 0:
        return flec,abc
    delt = (n2/n1)**2*(1+(dPane/dNormal)**2)-1#判定全反射
    if delt>0:
        k =dPane/dNormal/np.sqrt(delt)
        fracDot = getSymDot(sPoint,normal,k)
        fracDot = getSymDot(fracDot,line)
        frac = getABC([cross,fracDot])
        return flec,frac
    return flec,[0,0,0]

函數cataDioLine則是反射折射的實現函數。註意，在此引入的getABC並不是此前定義的通過點和角度求表達式的函數，而是通過兩點轉[a,b,c]的函數。

那麼我們是否可以寫一個同名函數來實現不同的功能呢？很遺憾的是，Python不支持函數的重載，所以隻能將同名函數封裝在一起：

def getABC(*par):
    if len(par)==1:     #此時傳入的參數為點對dots=[(x0,y0),(x1,y1)]
        dots = par[0]
        abc = [dots[1][1]-dots[0][1],
                dots[0][0]-dots[1][0], 
                -np.linalg.det(dots)]
        return np.array(abc)/(np.sqrt(abc[0]**2+abc[1]**2))
    elif len(par)==2:   #此時傳入的參數為點和角度(x0,y0),theta
        theta,sPoint = par
        a,b = [np.sin(theta),-np.cos(theta)]
        c = -(a*sPoint[0]+b*sPoint[1])
        return [a,b,c]

看到輸入參數(*par)，我們很多人可能會產生某些不是很美妙的聯想，但不要興奮，這隻是python的一種傳參方式。(*args)表示將傳入的參數組成一個列表args；(**kargs)表示將傳入的參數組成一個字典kargs。

弧面問題

光線在弧面上的反射問題，是典型的那種看似復雜實則簡單的紙老虎問題，簡單到我們隻要找到法線就能輕松地轉化為平面問題。

所以，問題被簡單地轉化為求解圓的切線問題——這個切線即反射平面。由於數學過程過於簡單，就不寫公式瞭，讀者可以試著看代碼反推公式。

#獲取過交點的圓弧的切線
def getTangent(corss=[0,1],circle=[0,0,1]):
    a = corss[0]-circle[0]
    b = corss[1]-circle[1]
    c = -a*corss[0]-b*corss[1]
    return [a,b,c]

至此，我們就可以得到一個完整的折射反射問題的求解方案：

#光在直線或弧線表面的反折射
def cataDio(abc=[1,-1,1],dots=[(0,2),(2,2)],
            sPoint=[-2,-1],n1=1,n2=1.5):
    cross = getCross(abc,dots,sPoint)           #獲取交點
    if cross == []:
        return [],[],[]
    if len(dots)==3:
        line = getTangent(cross,arc2cir(dots))  #圓上切線
    elif len(dots)==2:
        line = getABC(dots)
    flec,frac = cataDioLine(abc,line,sPoint,cross,n1,n2)
    return cross,flec,frac

當然，這裡的getCross也需要重新寫成不僅適合直線，而且適合弧線的形式：

def getCross(abc=[1,-1,0],dots=[[0,-1],[0,1],[0.5,0]],point=[]):
    if len(dots)==3:
        return getCrossArc(abc,dots,point)
    if len(dots)==2:
        return getCrossDots(abc,dots,point)

這時我們發現用兩個點表示線段，三個點表示弧線還是比較舒服的一種做法，至少二者在表達形式上的統一似乎能為我們帶來某種內心的愉悅。

以上就是python光學仿真實現光線追跡折射與反射的實現的詳細內容，更多關於python光線追跡的資料請關註WalkonNet其它相關文章！

推薦閱讀：