Python演化計算基準函數詳解
基準函數是測試演化計算算法性能的函數集,由於大部分基準函數集都是C/C++編寫,Python編寫的基準函數比較少,因此本文實現瞭13個常用基準函數的Python版。
基準函數定義
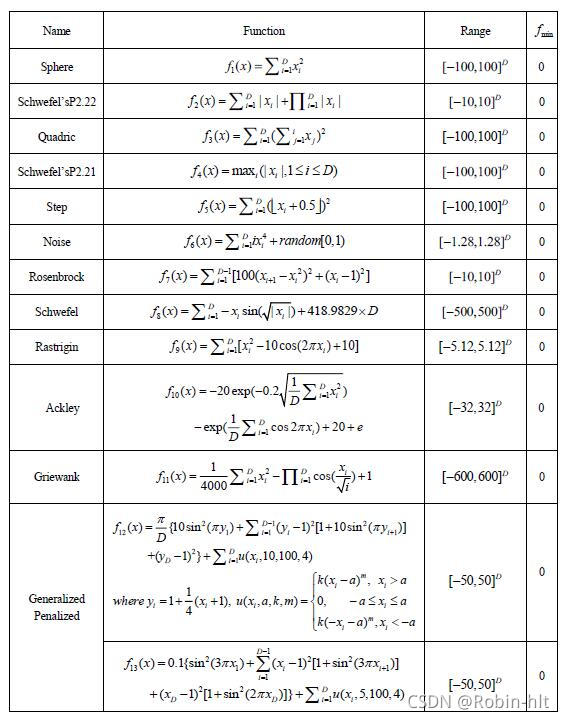
代碼實現
benchmark.py
import numpy as np
import copy
"""
Author : Robin_Hua
update time : 2021.10.14
version : 1.0
"""
class Sphere:
def __init__(self, x):
self.x = x
def getvalue(self):
res = np.sum(self.x**2)
return res
class Schwefel2_22:
def __init__(self, x):
self.x = x
def getvalue(self):
res = np.sum(np.abs(self.x)) + np.prod(np.abs(self.x))
return res
class Noise:
def __init__(self,x):
self.x = x
def getvalue(self):
d = self.x.shape[0]
res = np.sum(np.arange(1, d + 1) * self.x ** 4) + np.random.random()
return res
class Schwefel2_21:
def __init__(self,x):
self.x = x
def getvalue(self):
res = np.max(np.abs(self.x))
return res
class Step:
def __init__(self,x):
self.x = x
def getvalue(self):
res = np.sum(int(self.x + 0.5) ** 2)
return res
class Rosenbrock:
def __init__(self,x):
self.x = x
def getvalue(self):
d = self.x.shape[0]
res = np.sum(np.abs(100*(self.x[1:] - self.x[:-1]**2)**2 + (1 - self.x[:-1])**2))
return res
class Schwefel:
def __init__(self,x):
self.x = x
def getvalue(self):
d = self.x.shape[0]
res = 418.9829*d - np.sum(self.x * np.sin(np.sqrt(np.abs(self.x))))
return res
class Rastrigin:
def __init__(self,x):
self.x = x
def getvalue(self):
d = self.x.shape[0]
res = 10 * d + np.sum(self.x ** 2 - 10 * np.cos(2 * np.pi * self.x))
return res
class Ackley:
def __init__(self,x):
self.x = x
def getvalue(self):
d = self.x.shape[0]
res = - 20 * np.exp(-0.2 * np.sqrt(np.mean(self.x ** 2)))
res = res - np.exp(np.mean(np.cos(2 * np.pi * self.x))) + 20 + np.exp(1)
return res
class Griewank:
def __init__(self,x):
self.x = x
def getvalue(self):
d = self.x.shape[0]
i = np.arange(1, d + 1)
res = 1 + np.sum(self.x ** 2) / 4000 - np.prod(np.cos(self.x / np.sqrt(i)))
return res
class Generalized_Penalized:
def __init__(self,x):
self.x = x
def u(self,a,k,m):
temp = copy.deepcopy(self.x)
temp[-a <= temp.any() <= a] = 0
temp[temp > a] = k*(temp[temp > a]-a)**m
temp[temp < -a] = k * (-temp[temp < -a] - a) ** m
"""
temp = np.zeros_like(self.x)
d = self.x.shape[0]
for i in range(d):
if self.x[i]>a:
temp[i] = k*(self.x[i]-a)**m
elif self.x[i]<-a:
temp[i] = k * (-self.x[i] - a) ** m
else:
pass
"""
return temp
def getvalue(self):
d = self.x.shape[0]
y = 1+1/4*(self.x+1)
res = np.pi/d*(10*np.sin(np.pi*y[0])**2+np.sum((y[:-1]-1)**2*(1+10*np.sin(np.pi*y[1:])**2))+(y[-1]-1)**2)+np.sum(self.u(10,100,4))
return res
def benchmark_func(x,func_num):
func = func_list[func_num]
res = func(x)
return res
func_list = [Sphere,Schwefel2_22,Noise,Schwefel2_21,Step,Rosenbrock,Schwefel,Rastrigin,Ackley,Griewank,Generalized_Penalized]
調用方法
輸入為向量x和函數編號func_num
import benchmark import numpy as np vector = np.random.random(30) value = benchmark.benchmark_func(x=vector,func_num=0).getvalue()
總結
本篇文章就到這裡瞭,希望能夠給你帶來幫助,也希望您能夠多多關註WalkonNet的更多內容!
推薦閱讀:
- 初識python的numpy模塊
- Python數據分析 Numpy 的使用方法
- Python機器學習三大件之一numpy
- python數據分析Numpy庫的常用操作
- Python Numpy中ndarray的常見操作