Java 二叉樹遍歷特別篇之Morris遍歷
在前面,我們簡單提及過二叉樹的遍歷方式,有遞歸和非遞歸兩個版本的遍歷。仔細想一想,不管是遞歸的,還是非遞歸的遍歷,兩種版本的遍歷都是需要耗費大量的、額外的空間。比如當我們二叉樹的高度有100層,那麼遞歸時,系統就會一直壓棧,最壞情況下,一直要壓入100次遍歷的遞歸函數,因為此處的空間復雜度是跟這顆二叉樹的高度相關的。所以有人就在想,有沒有什麼方式,能夠使這個空間復雜度再壓縮一點呢?

前期文章:二叉樹的非遞歸遍歷
本期文章源碼:GitHub
有,肯定是有的。那就是今天的主題:Morris遍歷。這種思想就能使二叉樹的遍歷,空間復雜度為O(1)。那我們直接開始吧!
一、Morris
在講解之前,我們來分析一下。為什麼遍歷二叉樹需要壓棧?
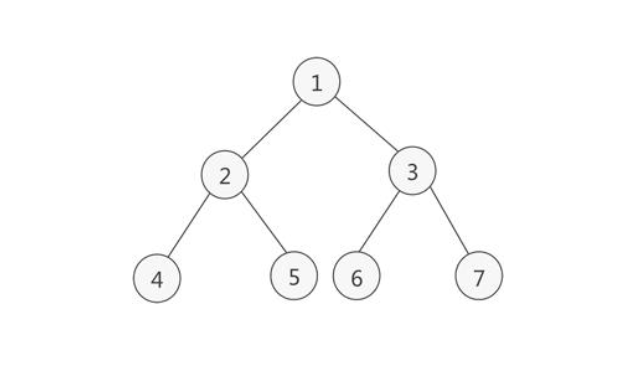
觀察上面這顆二叉樹,腦補一下。當我們一直往下遍歷時,走到值為4的節點,打印輸出4後,我該怎麼回到2節點? 每個節點都是隻有指向左右孩子的引用,並沒有指向父節點的引用。
所以在遍歷4節點的時候,會提前將2節點的所有信息,放入棧裡面,隻有在4節點遍歷完成之後,才會彈出棧裡的信息(2節點)。然後繼續遍歷其他的節點。
這也就是為什麼遍歷二叉樹需要壓棧的原因。
那麼我們就在想啊,有沒有種方法,能夠不壓棧,就能從4節點直接返回到2節點呢? 那就是利用4節點的右孩子引用。因為4節點是葉子節點,沒有左右孩子節點的。 我們將4節點的右孩子引用,指向2節點,這樣就能夠從4節點直接返回到2節點瞭。具體的圖片如下:

上圖橙色的線條,是Morris方法的作用,就是改變某些節點的右孩子引用。然後在具體的遍歷過程中,我們將橙色線條擦除即可。保證跟原二叉樹一模一樣。這就是Morris的思想。 那麼問題來瞭,我們該如何畫這些橙色的線條呢?
前提:我們準備兩個引用變量:cur和mostRight。 cur表示當前遍歷的節點;mostRight表示cur節點左子樹中,往右邊遍歷,第一個沒有右孩子的節點。舉個例子:上圖中cur是1節點,則mostRight就是1節點左子樹中,往右下角遍歷,5節點就是第一個沒有右孩子的節點。
Morris遍歷細節:(cur初始化為根結點)
如果cur沒有左孩子,cur就向右孩子移動。(cur = cur.right)
如果cur有左孩子,那就找到cur左子樹中,最靠右的節點mostRight:
- 如果mostRight的右孩子是null,說明是第一次遍歷到mostRight。此時讓mostRight的右孩子指向cur。
- 如果mostRight的右孩子是cur,說明是第二次遍歷到mostRight。此時讓mostRight的右孩子等於null即可。
遍歷結束條件:cur等於null時
偽代碼:
public void morris(Node root) {
if (root == null) {
return;
}
Node cur = root;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight 不等於null) {
1、循環找到mostRight節點
2、判斷mustRight的右孩子是否為null
}
//mostRight等於null時
cur = cur.right; //向右子樹移動
}
}
上面的偽代碼就是大致的框架結構,具體的代碼如下:
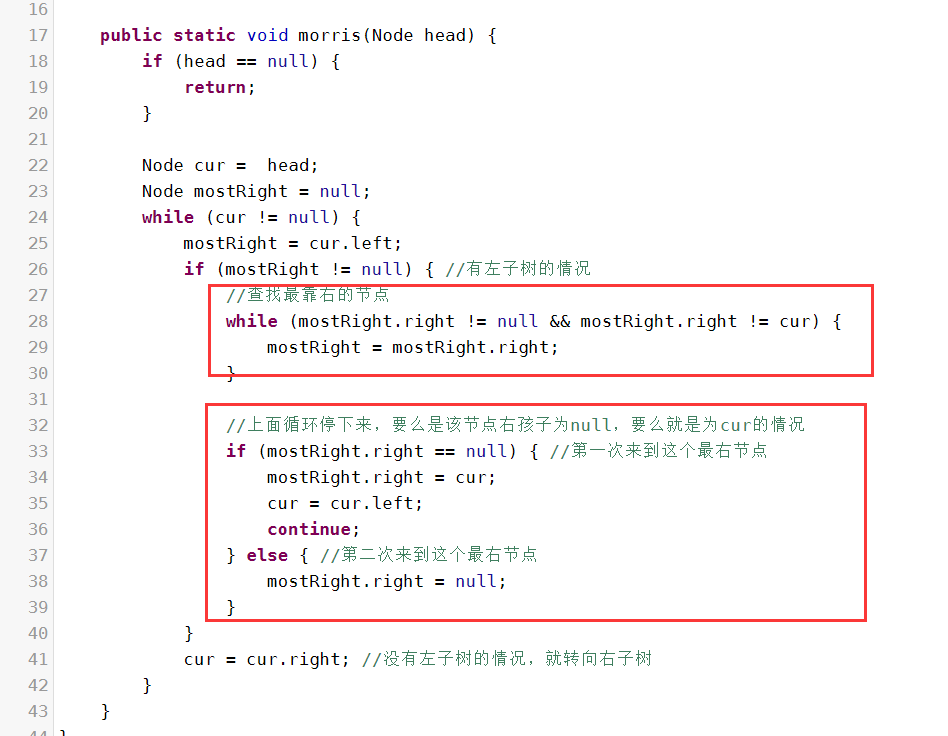
值得註意的是,當第一次遍歷到mostRight時,讓mostRight的右孩子指向cur之後,cur 再往左子樹走,然後應該再寫一句continue。讓代碼繼續往cur的左子樹繼續遍歷。
可能有的同學分不清,什麼時候是第一次遍歷到mostRight,什麼是第二次遍歷到mostRight。簡單點說,第一次就是mostRight的右孩子是null時,此時我們需要將右孩子指向cur;第二次是mostRight的右孩子指向cur的時候,此時我們需要將右孩子重新改回來,改為null。
關於前序、中序、後序遍歷,都是在Morris的基礎之上,添加printf即可。具體的,請往下看。
二、前序遍歷
我們都知道前序遍歷的順序是:頭左右。
而Morris改前序遍歷,非常簡單。記住兩個點,你就能獨自改前序遍歷。
- 如果cur節點沒有左孩子,那就打印當前cur的值
- 如果是第一次遍歷到mostRight節點,那就打印當前cur的值
就以上兩個點,添加到代碼裡面即可。

其他的代碼,原封不動。隻添加這兩句代碼即可完成前序遍歷。
三、中序遍歷
前序遍歷順序:左頭右。
中序跟前序的遍歷,這裡很相似,也是記住兩個點即可:
- 如果cur沒有左孩子,直接打印輸出cur的值
- 如果mostRight是第二次遍歷到,那就打印輸出cur的值
跟前序遍歷的區別隻是mostRight這裡,前序是第一次遍歷到mostRight就打印cur,中序是第二次遍歷到就打印。

當然,這兩個printf可以提取出來,寫一行即可。這裡隻是為瞭讓大傢清晰地認識到中序遍歷。
四、後序遍 歷(較難)
Morris改後序遍歷,稍微有一點點難,因為Morris遍歷出來的左右結果,都滿足一個規律:當前節點沒有左子樹,那麼隻會遍歷一次這個節點;當前節點有左子樹,那麼會有mostRight節點會返回到cur節點,也就是說有左孩子的節點,會遍歷兩次。
後序遍歷是每個節點,遍歷到第3次的時候,才打印輸出,現在可好,Morris遍歷最多隻能遍歷到2次,那該如何是好???
不急,我們來看一張圖:

不難發現,紅色的數值就是後序遍歷的結果。對比下左邊的二叉樹,紅色線條的指向,從左到右,從下到上的打印順序,竟然跟後序遍歷的結果是一樣的。
那我們就以這個為切入點,當遍歷cur的時候,我們就可以打印cur左子樹的最靠右的那一排的節點。比如cur等於1節點的時候,我們就可以打印2、5節點。
要滿足從下到上的打印順序,最容易想到的就是搞一個棧,壓棧進行,然後再依次彈出棧並打印。這樣的話,空間復雜度就不是O(1)瞭。 大傢是否還記得逆序單鏈表?我們將那一排的節點,進行逆序,然後打印輸出之後,再逆序回來即可。
//逆序那一排節點
public Node reverseList(Node node) {
Node pre = null;
Node next = null;
while (node != null) {
next = node.right; //逆序右子樹那一排節點
node.right = pre;
pre = node;
node = next;
}
return pre;
}
逆序完成之後,打印輸出即可,然後在逆序回來,保持原來的狀態
public void printList(Node node) {
Node newHead = reverseList(node); //逆序
node = newHead; //先保存newHead,等會逆序
while (newHead != null) {
System.out.print(newHead.val + " ");
newHead = newHead.right; //向右子樹走
}
reverseList(node); //逆序回來,保持原狀態
}
上面兩個方法,就能實現打印行為。現在的問題是,怎麼進行調用???
Morris遍歷,有的節點會遍歷到一次,而有的節點會遍歷到兩次。牢牢抓住這兩種情況,Morris遍歷就簡單瞭。
這裡的後序遍歷,還是跟前序和中序差不多,隻是打印函數,我們在第二次遍歷到mostRight調用即可。
比如:在上圖中,第二次遍歷到mostRight等於4節點時,我們就調用打印函數,傳遞的參數是cur的左孩子。再比如:第二次遍歷到mostRight等於5節點時,此時調用printList(cur.left),此時的cur是1節點。
看代碼更清晰:

最後切記,當24行~43行的循環結束後,還剩下整棵樹的最靠右的那一排節點沒有打印(對應上圖就是:1、3、7節點還沒打印),要單獨調用打印函數,傳遞根結點即可。
好啦,以上全部就是Morris遍歷二叉樹的全部情況,牢牢抓住cur節點有沒有左子樹的情況,應該就能很好理解瞭。

到此這篇關於Java 二叉樹遍歷特別篇之Morris遍歷的文章就介紹到這瞭,更多相關Java 二叉樹遍歷 內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!