詳談浮點精度(float、double)運算不精確的原因
為什麼浮點精度運算會有問題
我們平常使用的編程語言大多都有一個問題——浮點型精度運算會不準確。比如
double num = 0.1 + 0.1 + 0.1; // 輸出結果為 0.30000000000000004 double num2 = 0.65 - 0.6; // 輸出結果為 0.05000000000000004
筆者在測試的時候發現 C/C++ 竟然不會出現這種問題,我最初以為是編譯器優化,把這個問題解決瞭。但是 C/C++ 如果能解決其他語言為什麼不跟進?根據這個問題的產生原因來看,編譯器優化解決這個問題邏輯不通。後來發現是打印的方法有問題,打印輸出方法會四舍五入。使用 printf(“%0.17f\n”, num); 以及 cout << setprecision(17) << num2 << endl; 多打印幾位小數即可看到精度運算不準確的問題。
那麼精度運算不準確這是為什麼呢?
我們接下來就需要從計算機所有數據的表現形式二進制說起瞭。如果大傢很瞭解二進制與十進制的相互轉換,那麼就能輕易的知道精度運算不準確的問題原因是什麼瞭。如果不知道就讓我們一起回顧一下十進制與二進制的相互轉換流程。
一般情況下二進制轉為十進制我們所使用的是按權相加法。十進制轉二進制是除2取餘,逆序排列法。很熟的同學可以略過。
// 二進制到十進制 10010 = 0 * 2^0 + 1 * 2^1 + 0 * 2^2 + 0 * 2^3 + 1 * 2^4 = 18 // 十進制到二進制 18 / 2 = 9 .... 0 9 / 2 = 4 .... 1 4 / 2 = 2 .... 0 2 / 2 = 1 .... 0 1 / 2 = 0 .... 1 10010
那麼,問題來瞭十進制小數和二進制小數是如何相互轉換的呢?
十進制小數到二進制小數一般是整數部分除 2 取餘,逆序排列,小數部分使用乘 2 取整數位,順序排列。二進制小數到十進制小數還是使用按權相加法。
// 二進制到十進制 10.01 = 1 * 2^-2 + 0 * 2^-1 + 0 * 2^0 + 1 * 2^1 = 2.25 // 十進制到二進制 // 整數部分 2 / 2 = 1 .... 0 1 / 2 = 0 .... 1 // 小數部分 0.25 * 2 = 0.5 .... 0 0.5 * 2 = 1 .... 1 // 結果 10.01
轉小數我們也瞭解瞭,接下來我們回歸正題,為什麼浮點運算會有精度不準確的問題。接下來我們看一個簡單的例子 2.1 這個十進制數轉成二進制是什麼樣子的。
2.1 分成兩部分 // 整數部分 2 / 2 = 1 .... 0 1 / 2 = 0 .... 1 // 小數部分 0.1 * 2 = 0.2 .... 0 0.2 * 2 = 0.4 .... 0 0.4 * 2 = 0.8 .... 0 0.8 * 2 = 1.6 .... 1 0.6 * 2 = 1.2 .... 1 0.2 * 2 = 0.4 .... 0 0.4 * 2 = 0.8 .... 0 0.8 * 2 = 1.6 .... 1 0.6 * 2 = 1.2 .... 1 0.2 * 2 = 0.4 .... 0 0.4 * 2 = 0.8 .... 0 0.8 * 2 = 1.6 .... 1 0.6 * 2 = 1.2 .... 1 ............
落入無限循環結果為 10.0001100110011…….. , 我們的計算機在存儲小數時肯定是有長度限制的,所以會進行截取部分小數進行存儲,從而導致計算機存儲的數值隻能是個大概的值,而不是精確的值。
從這裡看出來我們的計算機根本就無法使用二進制來精確的表示 2.1 這個十進制數字的值,連表示都無法精確表示出來,計算肯定是會出現問題的。
精度運算丟失的解決辦法
現有有三種辦法
- 如果業務不是必須非常精確的要求可以采取四舍五入的方法來忽略這個問題。
- 轉成整型再進行計算。
- 使用 BCD 碼存儲和運算二進制小數(感興趣的同學可自行搜索學習)。
一般每種語言都用高精度運算的解決方法(比一般運算耗費性能),比如 Python 的 decimal 模塊,Java 的 BigDecimal,但是一定要把小數轉成字符串傳入構造,不然還是有坑,其他語言大傢可以自行尋找一下。
# Python 示例
from decimal import Decimal
num = Decimal('0.1') + Decimal('0.1') + Decimal('0.1')
print(num)
// Java 示例
import java.math.BigDecimal;
BigDecimal add = new BigDecimal("0.1").add(new BigDecimal("0.1")).add(new BigDecimal("0.1"));
System.out.println(add);
拓展:詳解浮點型
上面既然提到瞭浮點型的存儲是有限制,那麼我們看一下我們的計算機是如何存儲浮點型的,是不是真的正如我們上面提到的有小數長度的限制。
那我們就以 Float 的數據存儲結構來說,根據 IEEE 標準浮點型分為符號位,指數位和尾數位三部分(各部分大小詳情見下圖)。
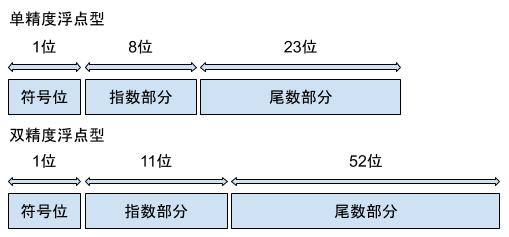
IEEE 754 標準
一般情況下我們表示一個很大或很小的數通常使用科學記數法,例如:1000.00001 我們一般表示為 1.00000001 * 10^3,或者 0.0001001 一般表示為 1.001 * 10^-4。
符號位
0 是正數,1 是負數
指數位
指數很有意思因為它需要表示正負,所以人們創造瞭一個叫 EXCESS 的系統。這個系統是什麼意思呢?它規定 最大值 / 2 – 1 表示指數為 0。我們使用單精度浮點型舉個例子,單精度浮點型指數位一共有八位,表示的十進制數最大就是 255。那麼 255 / 2 – 1 = 127,127 就代表指數為 0。如果指數位存儲的十進制數據為 128 那麼指數就是 128 – 127 = 1,如果存儲的為 126,那麼指數就是 126 – 127 = -1。
尾數位
比如上述例子中 1.00000001 以及 1.001 就屬於尾數,但是為什麼叫尾數呢?因為在二進制中比如 1.xx 這個小數,小數點前面的 1 是永遠存在的,存瞭也是浪費空間不如多存一位小數,所以尾數位隻會存儲小數部分。也就是上述例子中的 00000001 以及 001 存儲這樣的數據。

IEEE 754 標準
通過上述程序我們得到的存儲 1.25 的 float 二進制結構的具體值為 00111111101000000000000000000000 ,我們拆分一下 0 為符號位他是個正值。01111111 為指數位,01000000000000000000000 是尾數。接下來我們驗證一下 01111111 轉為十進制是 127,那麼經過計算指數為 0。尾數是 01000000000000000000000 加上默認省略的 1 為 1.01(省略後面多餘的 0),轉換為十進制小數就是 1.25。
以上為個人經驗,希望能給大傢一個參考,也希望大傢多多支持WalkonNet。
推薦閱讀:
- Python浮點數取整、格式化和NaN處理的操作方法
- Java精確計算BigDecimal類詳解
- Java BigDecimal案例詳解
- Java學習筆記:關於Java double類型相加問題
- java BigDecimal類案例詳解