C語言數據結構與算法之圖的遍歷(一)
引入
在數據結構中常見的有深度優先搜索和廣度優先搜索。為什麼叫深度和廣度呢?其實是針對圖的遍歷而言的,請看下面這個圖:
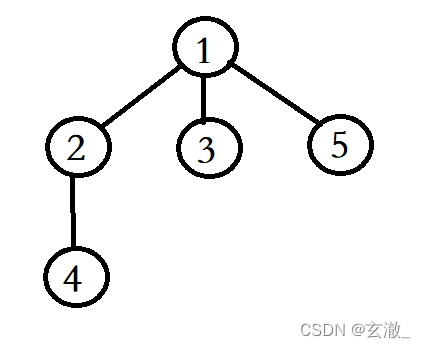
圖是由一些小圓點(稱為頂點) 和 連接這些點的直線 (稱為邊)組成的。
例如上圖就是由5個頂點(編號為 1,2,3,4,5) 和5條邊(1-2,1-3,1-4,2-4)組成。
現在我們從1號頂點開始遍歷這個圖,遍歷就是把圖的每一個頂點都訪問一次。使用深度優先搜索將會得到如下的結果。
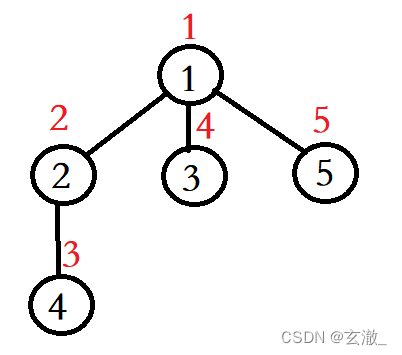
圖中每個頂點旁邊的數表示這個頂點是第幾個被訪問到的,我們稱之為 —— 時間戳
深度優先搜索
使用深度優先搜索來遍歷這個圖的過程:
首先從一個未走過的頂點作為起始頂點,比如以1號頂點作為起點。沿1號頂點的邊去嘗試其他它未走過的頂點,首先發現的是2號頂點還沒被走過,於是來到瞭2號頂點。
再以2號頂點作為出發點繼續嘗試訪問其他未走到過的頂點,這樣又來到瞭4號頂點。
再以4號頂點作為出發點繼續嘗試訪問其他未走過的頂點。但是,此時在4號頂點的周圍已經沒有其他的頂點瞭,所以需要返回到2號頂點。返回到2號頂點後,發現沿2號頂點也不能在訪問到其他未走到的點瞭,此時又需要返回到1號頂點。
繼續以1號頂點嘗試訪問其他頂點,我們來到瞭3號點。以此類推,我們最後來到瞭5號點。到此,所以的頂點都走過瞭,遍歷結束
深度優先搜索的主要思想是:
首先以一個未被訪問的頂點作為起始頂點,沿當前頂點的邊走到未被訪問過的頂點
當沒有未訪問過的頂點時,則回到上一個頂點,繼續試探訪問別的頂點,直到所有的頂點都被訪問過。
顯然,深度優先搜索是沿著圖的某一條分支遍歷直至末端,然後回溯,再沿另一條實現相同的遍歷,直到所以的頂點都被訪問完為止。
代碼實現
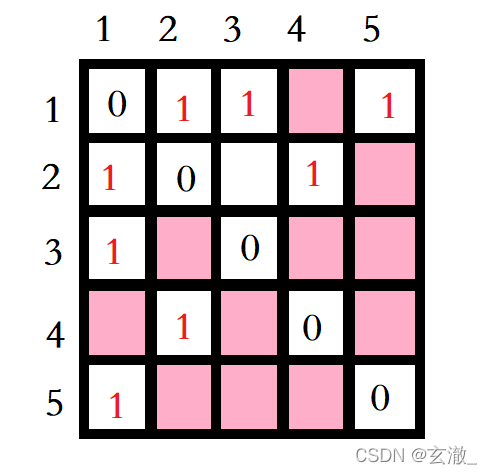
上面的二維數組中 第i行第j列就是表示頂點i到頂點j是否有邊。
1表示有邊,x表示沒有邊,0表示頂點自己到自己。
我們將這種方法稱為 —— 圖的鄰接矩陣儲存法。
細心的朋友可能會發現這張圖沿著對角線全部是0,因為上面這張圖是 無向圖。
所謂無向圖就是指圖的邊沒有方向。例如邊 1 – 5 表示 1號頂點可以到 5號頂點,5號頂點也可以到1號頂點。
接下來就是解決怎麼用深度優先搜索來實現遍歷瞭:
void dfs(int cur) //cur是當前所在的頂點編號
{
printf("%d", cur);
sum++; //每訪問一個點就sum++
if (sum == n) return; //所有的頂點都訪問過瞭
for (i = 1; i <= n; i++) //從1到n的頂點依次嘗試,看看有哪些頂點與當前頂點cur有邊相連
{
//判斷當前頂點cur到頂點i是否有邊,並判斷頂點i是否已被訪問過
{
if (e[cur][i] == 1 && book[i] == 0)
{
book[i] = 1; //標記頂點i已經訪問過
dfs(i); //從頂點i出發繼續遍歷
}
}
}
return;
}
在上面的代碼中 變量 cur 存儲的是當前正在遍歷的點,二維數組e存儲的就是圖的邊(鄰接矩陣),數組book用來標記哪些頂點已經訪問過,變量sum用來記錄已經訪問多少個頂點,變量你存儲的是圖的頂點總個數。
完整代碼
#include <stdio.h>
int book[101], sum, n, e[101][101];
void dfs(int cur) //cur是當前所在的頂點編號
{
printf("%d", cur);
sum++; //每訪問一個點就sum++
if (sum == n) return; //所有的頂點都訪問過瞭
for (i = 1; i <= n; i++) //從1到n的頂點依次嘗試,看看有哪些頂點與當前頂點cur有邊相連
{
//判斷當前頂點cur到頂點i是否有邊,並判斷頂點i是否已被訪問過
{
if (e[cur][i] == 1 && book[i] == 0)
{
book[i] = 1; //標記頂點i已經訪問過
dfs(i); //從頂點i出發繼續遍歷
}
}
}
return;
}
int main()
{
int i, j, m, a, b;
scanf("%d %d", &n, &m);
//初始化二維矩陣
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if (i == j) e[i][j] = 0;
else e[i][j] = 99999999; //我們假設99999999為x
//讀入頂點之間的邊
for (i = 1; i <= n; i++)
{
scanf("%d %d", &a, &b);
e[a][b] = 1;
e[b][a] = 1; //因為該圖為無向圖
}
//從1號頂點出發
book[1] = 1; //標記1號頂點已經訪問
dfs(1); //從1號頂點開始遍歷
return 0;
}
到此這篇關於C語言數據結構與算法之圖的遍歷(一)的文章就介紹到這瞭,更多相關C語言數據結構 圖的遍歷內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!