Java實現赫夫曼樹(哈夫曼樹)的創建
一、赫夫曼樹是什麼?
給定N個權值作為N個葉子結點,構造一棵二叉樹,若該樹的帶權路徑長度(WPL)達到最小,稱這樣的二叉樹為最優二叉樹,也稱為哈夫曼樹(Huffman Tree)。哈夫曼樹是帶權路徑長度最短的樹,權值較大的結點離根較近。
圖1 一棵赫夫曼樹
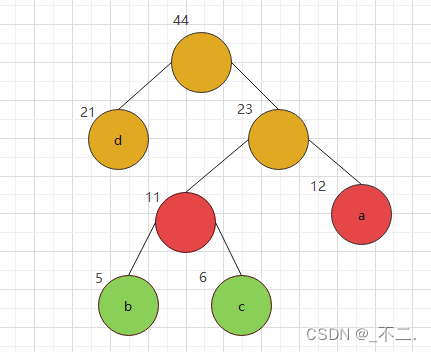
1.路徑和路徑長度
在一棵樹中,從一個結點往下可以達到的孩子或孫子結點之間的通路,稱為路徑。
例如圖1根節點到b節點之間的通路稱為一條路徑。
在一條路徑中,每經過一個結點,路徑長度都要加 1 。若規定根結點的層數為1,則從根結點到第L層結點的路徑長度為L-1。
例如圖1根節點到c節點的路徑長度為 4 – 1 = 3
2.節點的權和帶權路徑長度
若將樹中結點賦給一個有著某種含義的數值,則這個數值稱為該結點的權。
例如圖1中abcd節點的權值分別為12、5、6、21
結點的帶權路徑長度為:從根結點到該結點之間的路徑長度與該結點的權的乘積。
例如圖1節點c的帶權路徑長度為 3 * 6 = 18
3.樹的帶權路徑長度
樹的帶權路徑長度規定為所有葉子結點的帶權路徑長度之和,記為WPL。
例如上圖中的樹的WPL = (5 + 6)* 3 + 12 * 2 + 21 = 78
二、創建赫夫曼樹
1.圖文創建過程
假設有n個權值,則構造出的哈夫曼樹有n個葉子結點。 n個權值分別設為 w1、w2、…、wn,則哈夫曼樹的構造規則為:

例如有四個葉子節點 a b c d 權值分別為 12、5、6、21
創建赫夫曼樹前森林如下
(1) 將w1、w2、…,wn看成是有n 棵樹的森林(每棵樹僅有一個結點);
(2) 在森林中選出兩個根結點的權值最小的樹合並,作為一棵新樹的左、右子樹,且新樹的根結點權值為其左、右子樹根結點權值之和;
在森林中取出 b c節點 形成一棵新樹M
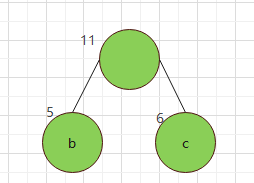
(3)從森林中刪除選取的兩棵樹,並將新樹加入森林;
將新樹M添加到森林後 森林如下
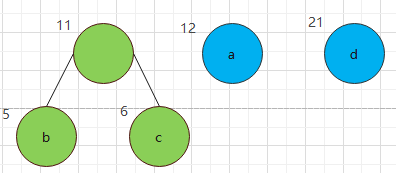
(4)重復(2)、(3)步,直到森林中隻剩一棵樹為止,該樹即為所求得的哈夫曼樹。
** 4.1重復步驟(2)
在森林中取出權為11的節點以及a節點組成一棵新樹N
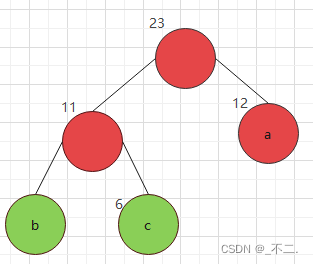
** 4.2重復步驟(3)
將新樹N添加到森林中 森林如下
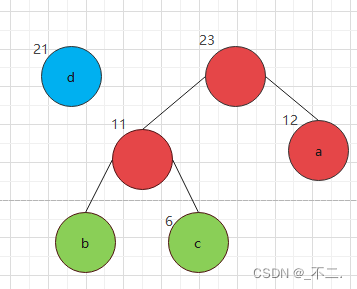
** 4.3重復步驟(2)
在森林中取出b節點和權為23的節點組成一棵新樹S
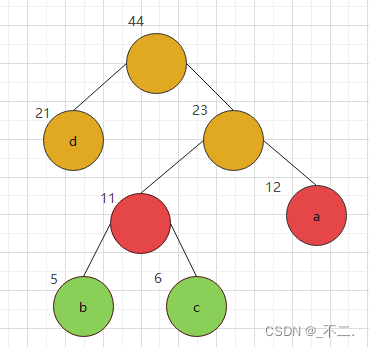
則新樹S就是我們要創建的赫夫曼樹
2.代碼實現
創建赫夫曼樹的過程中,為確保每次從森林中取出的節點為最小值,這裡采用快速排序算法,每次取出節點前,將森林中的樹按照權值從小到大重新排列一次
節點的結構如下:
class Node implements Comparable<Node> {
private int element; //節點的權
private Node left; //節點的左子樹
private Node right; //節點的右子樹
//構造器
public Node(int aElement) {
this.element = aElement;
}
public int getElement() {
return element;
}
public void setElement(int element) {
this.element = element;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
//前序遍歷
public void preOrder() {
System.out.print(this + " ");
if (this.getLeft() != null) {
this.getLeft().preOrder();
}
if (this.getRight() != null) {
this.getRight().preOrder();
}
}
@Override
public String toString() {
return element + "";
}
@Override
public int compareTo(Node o) {
return this.getElement() - o.getElement(); //從小大到排序
}
}
完整代碼如下:
package com.xx.huffmantree;
import java.util.*;
/**
* @author 謝鑫
* @version 1.0
* @date 2021/12/7 16:31
* 赫夫曼樹
*/
public class HuffmanTreeDemo {
public static void main(String[] args) {
int[] arr = {12, 5, 6, 21};
HuffmanTree huffmanTree = new HuffmanTree();
Node root = huffmanTree.creTree(arr);
huffmanTree.preOrder(root);
}
}
class HuffmanTree {
public Node creTree(int[] aArr) {
List<Node> list = new ArrayList<>(); //用於存放數組元素
//將數組放存放list中
for (int element : aArr) {
list.add(new Node(element));
}
while (list.size() > 1) { //循環創建樹
Collections.sort(list); //從小到大排序
//從list中從小取出兩個節點
Node left = list.get(0);
Node right = list.get(1);
//初始化小樹根節點
Node root = new Node(left.getElement() + right.getElement()); //小樹根節點為左右子樹節點element值的和
//構建小樹
root.setLeft(left);
root.setRight(right);
list.add(root); //將小樹根節點再次添加到list中
//移除集合中已經參與構建過樹的節點
list.remove(left);
list.remove(right);
// list.remove(0);
// list.remove(0); //取出兩個隊頭元素 也可
}
return list.get(0);
}
//前序遍歷
public void preOrder(Node aRoot) {
if (aRoot != null) {
aRoot.preOrder();
} else {
System.out.println("此樹為空, 無法完成前序遍歷!");
}
}
}
class Node implements Comparable<Node> {
private int element; //節點的權
private Node left; //節點的左子樹
private Node right; //節點的右子樹
//構造器
public Node(int aElement) {
this.element = aElement;
}
public int getElement() {
return element;
}
public void setElement(int element) {
this.element = element;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
//前序遍歷
public void preOrder() {
System.out.print(this + " ");
if (this.getLeft() != null) {
this.getLeft().preOrder();
}
if (this.getRight() != null) {
this.getRight().preOrder();
}
}
@Override
public String toString() {
return element + "";
}
@Override
public int compareTo(Node o) {
return this.getElement() - o.getElement(); //從小大到排序
}
}
最後我們采用前序遍歷輸出我們創建的赫夫曼樹,結果如下

到此這篇關於Java實現赫夫曼樹(哈夫曼樹)的創建的文章就介紹到這瞭,更多相關Java赫夫曼樹內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!