MATLAB 如何求取離散點的曲率最大值
我就廢話不多說瞭,大傢還是直接看代碼吧~
x0 = linspace(0.1,2,100);%x0,y0驗證函數離散點,可以非等間隔
y0 = 1./x0;
h1 = abs(diff(x0)) ;
h = [h1 h1(end)];
ht = h;
yapp1 = gradient(y0)./ht; %matlab數值近似
yapp2 = del2(y0)./ht; %matlab數值近似
k2 = abs(yapp2)./(1+yapp1.^2).^(3/2);
figure
plot(k2)
title('曲率曲線')
[~,maxFlag] = max(k2);%曲率最大位置
x_max = x0(maxFlag);
y_max = y0(maxFlag);
%畫出圖像 標註曲率最大點
figure
plot(x0,y0,'.-');
hold on;
plot(x_max,y_max,'rp')
title('標註最大曲率點')
xlabel('log10((norm(B*Xk-L)))')
ylabel('log10((norm(Xk)))')

補充:MATLAB 插值+計算離散點曲率
思路:點足夠密的話直接用 diff、gradient 求曲率,稀疏的話先插值再算曲率。
公式:
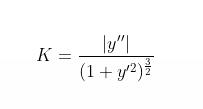
點密的情況 輸入曲線坐標(1-2)求一、二階導數(4-9)通過公式求得曲率(10)
x = 0:0.01:7;
y = cos(x*0.5*pi);
h1 = abs(diff(x));
h = [h1 h1(end)];
ht = h;
y1 = gradient(y)./ht;
y2 = gradient(y1)./ht;
curv = abs(y2)./sqrt((1+y1.^2).^3);
plot(x,y,'-',x,curv,'--r);
legend('Raw Data, 'Curvature','Location',"best");
grid on
圖像與下文理論值圖像相同
點稀疏的情況
1、輸入散點坐標(1-2)
2、用樣條曲線(B-Spline)等方法插值得到擬合曲線(3-4)
3、diff、gradient 函數求擬合曲線的一、二階導數(6-11)
4、通過公式求得曲率(12)
例:餘弦函數取 8 個點,用 B-Spline 插值
x = 0:1:7;
y = cos(x*0.5*pi);
xx = 0:0.01:7;
yy = spline(x,y,xx);
h1 = abs(diff(xx));
h = [h1 h1(end)];
ht = h;
yy1 = gradient(yy)./ht;
yy2 = gradient(yy1)./ht;
curv = abs(yy2)./sqrt((1+yy1.^2).^3);
plot(xx,yy,'-',xx,curv,'--r',x,y,'o-');
legend('B-Spline', 'Curvature','Raw Data','Location',"best");
grid on
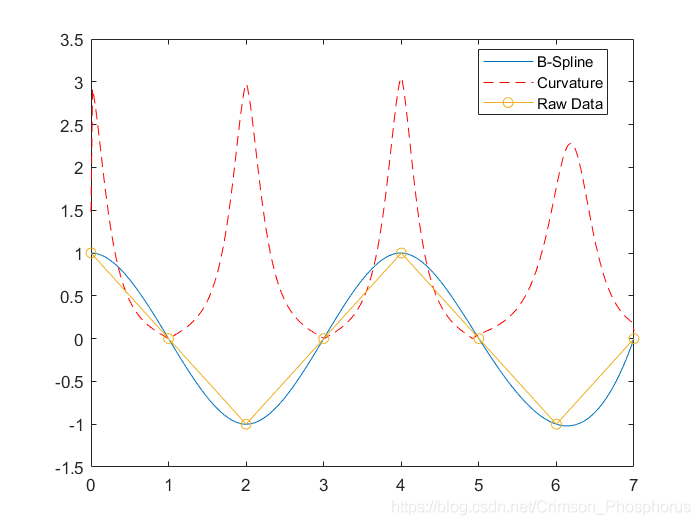
補充用法
求最大曲率並在圖中標出
[max_val,max_ind]=max(curv); hold on plot(xx(max_ind),yy(max_ind),'*r');
與理論值(餘弦函數曲線)對比
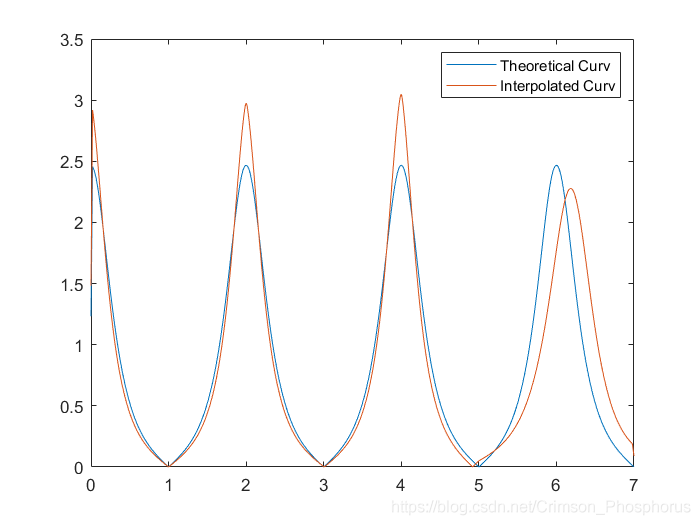
曲率對比
幾種插值方法對比
列舉四種方法,分別為:分段線性插值、三次樣條曲線(B-Spline)插值、三次 Hermite 插值(PCHIP)、修正 Akima 分段三次 Hermite 插值(Akima)
Case 1: 三維螺線
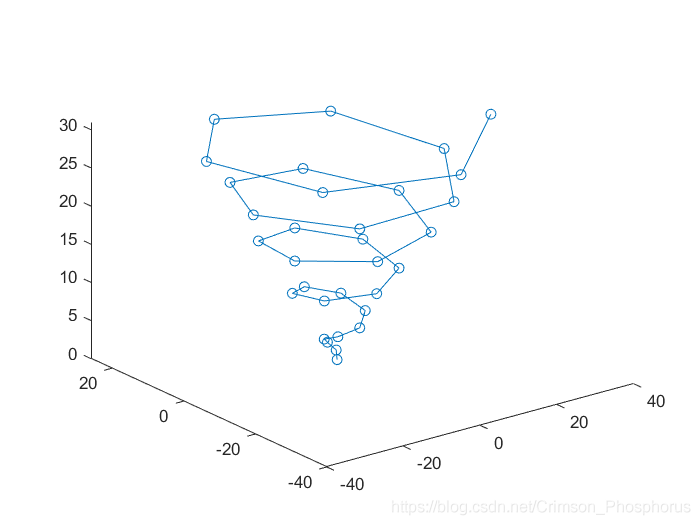
三維螺線散點
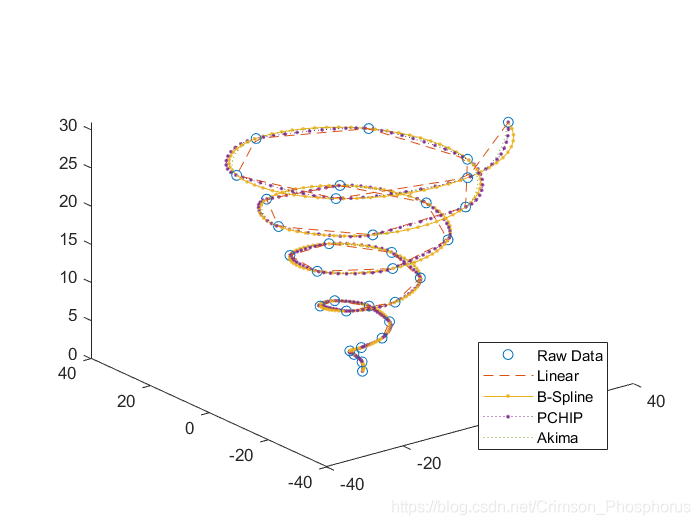
插值
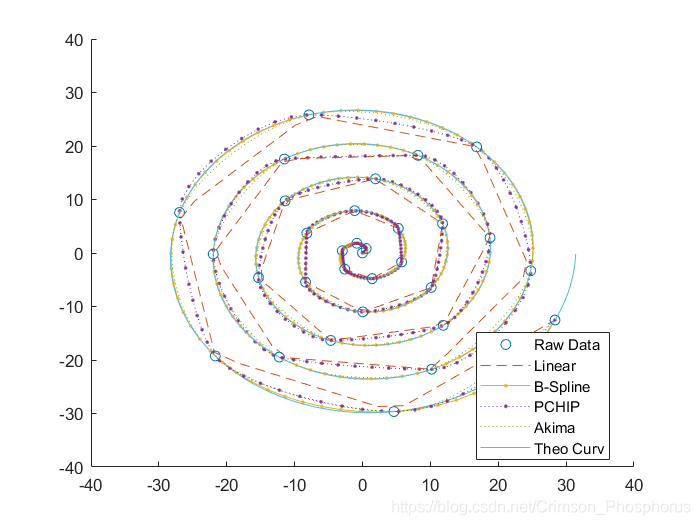
俯視
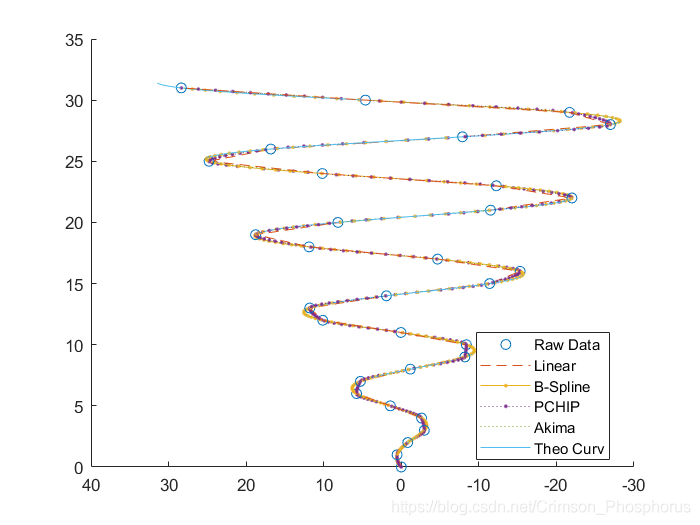
側視
Case 2:二維梯形波
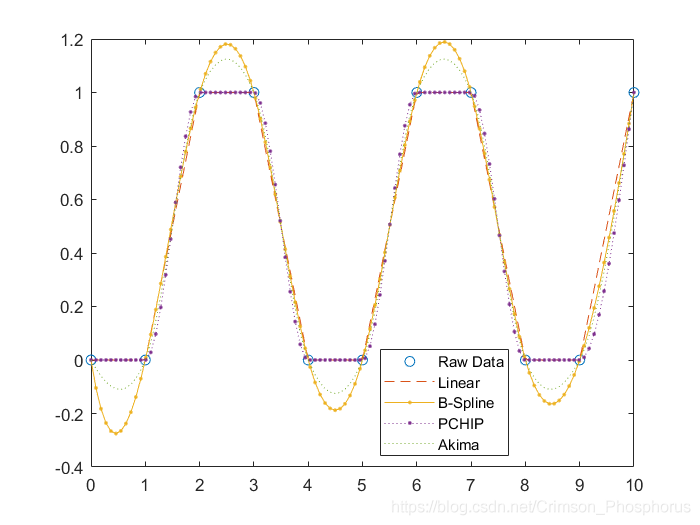
二維梯形波
Case 3:三維不規則折線
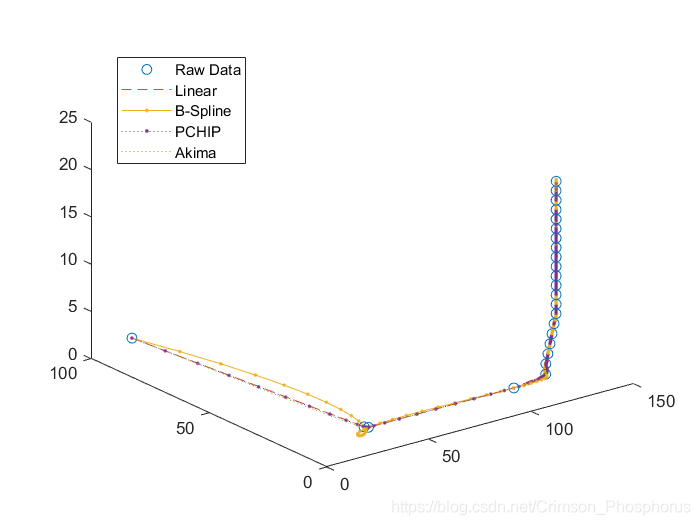
三維不規則折線(不等間距)
對比可得:
Case 1:B-Spline>Akima>PCHIP>Linear
Case 2:Linear>PCHIP>Akima>B-Spline
Case 3:Linear≈PCHIP≈Akima>B-Spline
故在插值的時候需要選擇適合的計算方法
以上為個人經驗,希望能給大傢一個參考,也希望大傢多多支持WalkonNet。如有錯誤或未考慮完全的地方,望不吝賜教。
推薦閱讀:
- None Found