AI:如何訓練機器學習的模型

1.Training: 如何訓練模型

一句話理解機器學習一般訓練過程 ：通過有標簽樣本來調整（學習）並確定所有權重Weights和偏差Bias的理想值。

訓練的目標：最小化損失函數

（損失函數下面馬上會介紹）

機器學習算法在訓練過程中，做的就是：檢查多個樣本並嘗試找出可最大限度地減少損失的模型；目標就是將損失(Loss)最小化

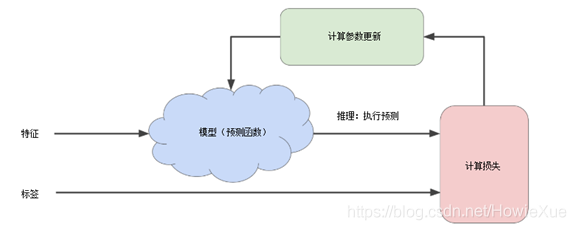
上圖就是一般模型訓練的一般過程（試錯過程），其中

• 模型： 將一個或多個特征作為輸入，然後返回一個預測 (y’) 作為輸出。為瞭進行簡化，不妨考慮一種采用一個特征並返回一個預測的模型，如下公式（其中b為 bias，w為weight）

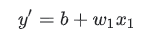
• 計算損失：通過損失函數，計算該次參數（bias、weight）下的loss。
• 計算參數更新：檢測損失函數的值，並為參數如bias、weight生成新值，以降低損失為最小。

例如：使用梯度下降法，因為通過計算整個數據集中w每個可能值的損失函數來找到收斂點這種方法效率太低。所以通過梯度能找到損失更小的方向，並迭代。

舉個TensorFlow代碼栗子，對應上面公式在代碼中定義該線性模型：

y_output = tf.multiply(w,x) + b

假設該模型應用於房價預測，那麼y_output為預測的房價，x為輸入的房子特征值（如房子位置、面積、樓層等）

2. Loss Function:損失和損失函數

損失是一個數值 表示對於單個樣本而言模型預測的準確程度。

如果模型的預測完全準確，則損失為零，否則損失會較大。

訓練模型的目標是從所有樣本中找到一組平均損失“較小”的權重和偏差。

損失函數的目標：準確找到預測值和真實值的差距

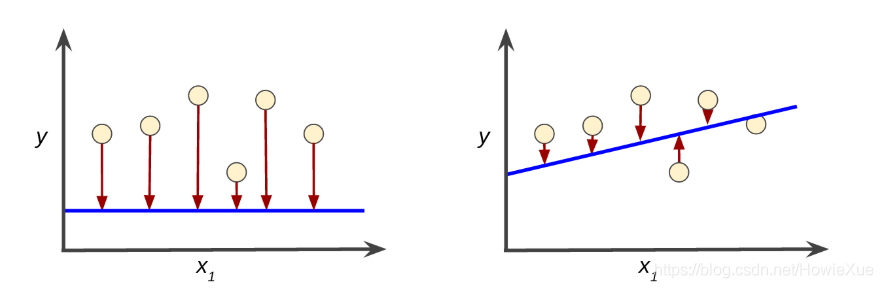
如圖 紅色箭頭表示損失，藍線表示預測。明顯左側模型的損失較大；右側模型的損失較小

要確定loss，模型必須定義損失函數 loss function。例如，線性回歸模型通常將均方誤差用作損失函數，而邏輯回歸模型則使用對數損失函數。

正確的損失函數，可以起到讓預測值一直逼近真實值的效果，當預測值和真實值相等時，loss值最小。

舉個TensorFlow代碼栗子，在代碼中定義一個損失loss_price 表示房價預測時的loss，使用最小二乘法作為損失函數：

loss_price = tr.reduce_sum(tf.pow(y_real - y_output), 2)

這裡，y_real是代表真實值，y_output代表模型輸出值（既上文公式的y’ ），因為有的時候這倆差值會是負數，所以會對誤差開平方，具體可以搜索下最小二乘法公式

3. Gradient Descent:梯度下降法

理解梯度下降就好比在山頂以最快速度下山：

好比道士下山，如何在一座山頂上，找到最短的路徑下山，並且確定最短路徑的方向

原理上就是凸形問題求最優解，因為隻有一個最低點；即隻存在一個斜率正好為 0 的位置。這個最小值就是損失函數收斂之處。

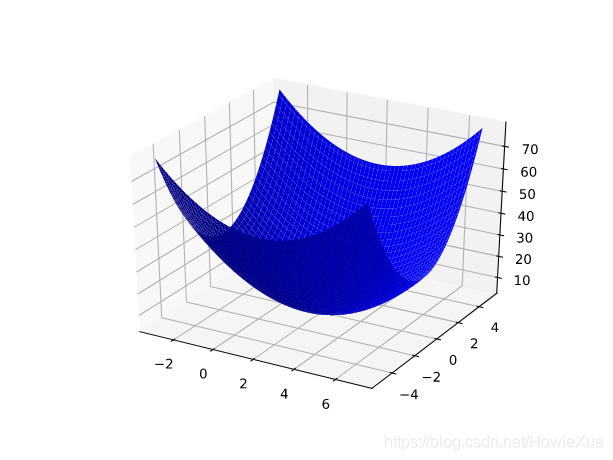
通過計算整個數據集中 每個可能值的損失函數來找到收斂點這種方法效率太低。我們來研究一種更好的機制，這種機制在機器學習領域非常熱門，稱為梯度下降法。

梯度下降法的目標：尋找梯度下降最快的那個方向

梯度下降法的第一個階段是為 選擇一個起始值（起點）。起點並不重要；因此很多算法就直接將 設為 0 或隨機選擇一個值。下圖顯示的是我們選擇瞭一個稍大於 0 的起點：

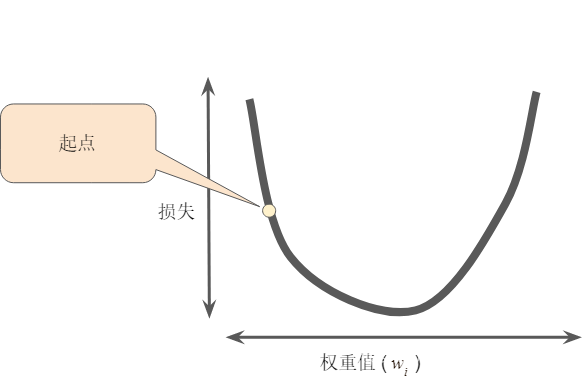
然後，梯度下降法算法會計算損失曲線在起點處的梯度。簡而言之，梯度是偏導數的矢量；它可以讓您瞭解哪個方向距離目標“更近”或“更遠”。請註意，損失相對於單個權重的梯度（如圖 所示）就等於導數。

請註意，梯度是一個矢量，因此具有以下兩個特征：

• 方向
• 大小

梯度始終指向損失函數中增長最為迅猛的方向。梯度下降法算法會沿著負梯度的方向走一步，以便盡快降低損失

為瞭確定損失函數曲線上的下一個點，梯度下降法算法會將梯度大小的一部分與起點相加

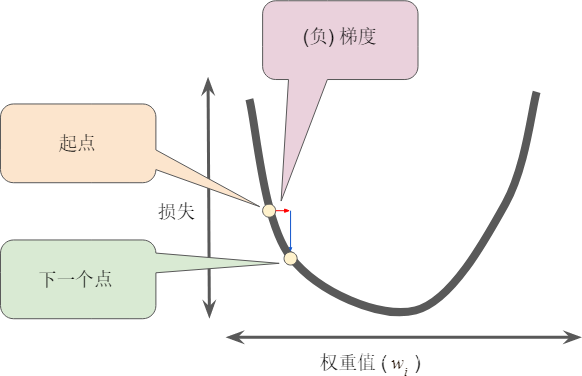
然後，梯度下降法會重復此過程，逐漸接近最低點。（找到瞭方向）

• 隨機梯度下降法SGD：解決數據過大，既一個Batch過大問題，每次迭代隻是用一個樣本（Batch為1），隨機表示各個batch的一個樣本都是隨機選擇。

4. Learning Rate:學習速率

好比上面下山問題中，每次下山的步長。

因為梯度矢量具有方向和大小，梯度下降法算法用梯度乘以一個稱為學習速率（有時也稱為步長）的標量，以確定下一個點的位置。這是超參數，用來調整AI算法速率

例如，如果梯度大小為 2.5，學習速率為 0.01，則梯度下降法算法會選擇距離前一個點 0.025 的位置作為下一個點。

超參數是編程人員在機器學習算法中用於調整的旋鈕。大多數機器學習編程人員會花費相當多的時間來調整學習速率。如果您選擇的學習速率過小，就會花費太長的學習時間：

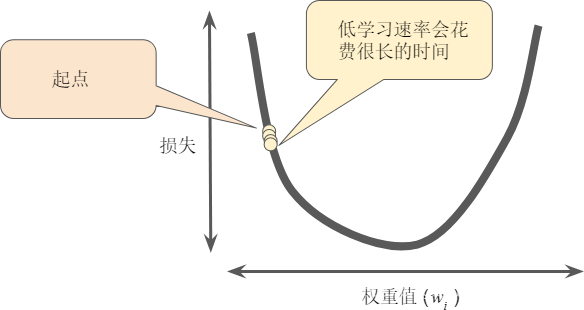
繼續上面的栗子，實現梯度下降代碼為：

train_step = tf.train.GradientDescentOptimizer(0.025).minimize(loss_price)

這裡設置梯度下降學習率為0.025, GradientDescentOptimizer()就是使用的隨機梯度下降算法， 而loss_price是由上面的損失函數獲得的loss

至此有瞭模型、損失函數以及梯度下降函數，就可以進行模型訓練階段瞭：

Session = tf.Session()
Session.run(init)
for _ in range(1000):
	Session.run(train_step, feed_dict={x:x_data, y:y_data}) 

這裡可以通過for設置固定的training 次數，也可以設置條件為損失函數的值低於設定值，

x_data y_data則為訓練所用真實數據，x y 是輸入輸出的placeholder（代碼詳情參見TensorFlow API文檔）

5. 擴展：BP神經網絡訓練過程

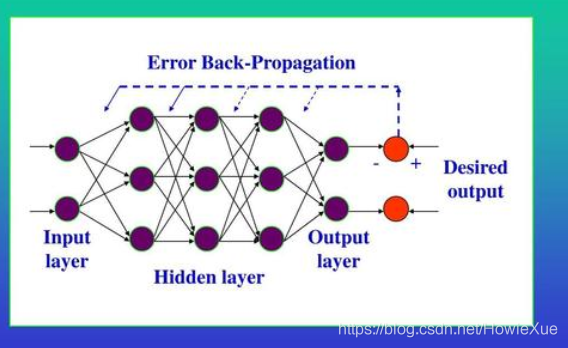
BP（BackPropagation）網絡的訓練，是反向傳播算法的過程，是由數據信息的正向傳播和誤差Error的反向傳播兩個過程組成。

反向傳播算法是神經網絡算法的核心，其數學原理是：鏈式求導法則

• 正向傳播過程：

輸入層通過接收輸入數據，傳遞給中間層（各隱藏層）神經元，每一個神經元進行數據處理變換，然後通過最後一個隱藏層傳遞到輸出層對外輸出。

• 反向傳播過程：

正向傳播後通過真實值和輸出值得到誤差Error，當Error大於設定值，既實際輸出與期望輸出差別過大時，進入誤差反向傳播階段：

Error通過輸出層，按照誤差梯度下降的方式，如上面提到的隨機梯度下降法SGD，反向修正各層參數（如Weights），向隱藏層、輸入層逐層反轉。

通過不斷的正向、反向傳播，直到輸出的誤差減少到預定值，或到達最大訓練次數。

到此這篇關於AI:如何訓練機器學習的模型的文章就介紹到這瞭,相信對你有所幫助，更多相關機器學習內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章，希望大傢以後多多支持WalkonNet！

推薦閱讀：

None Found