利用java實現二叉搜索樹
二叉搜索樹的定義
- 它是一顆二叉樹
- 任一節點的左子樹上的所有節點的值一定小於該節點的值
- 任一節點的右子樹上的所有節點的值一定大於該節點的值
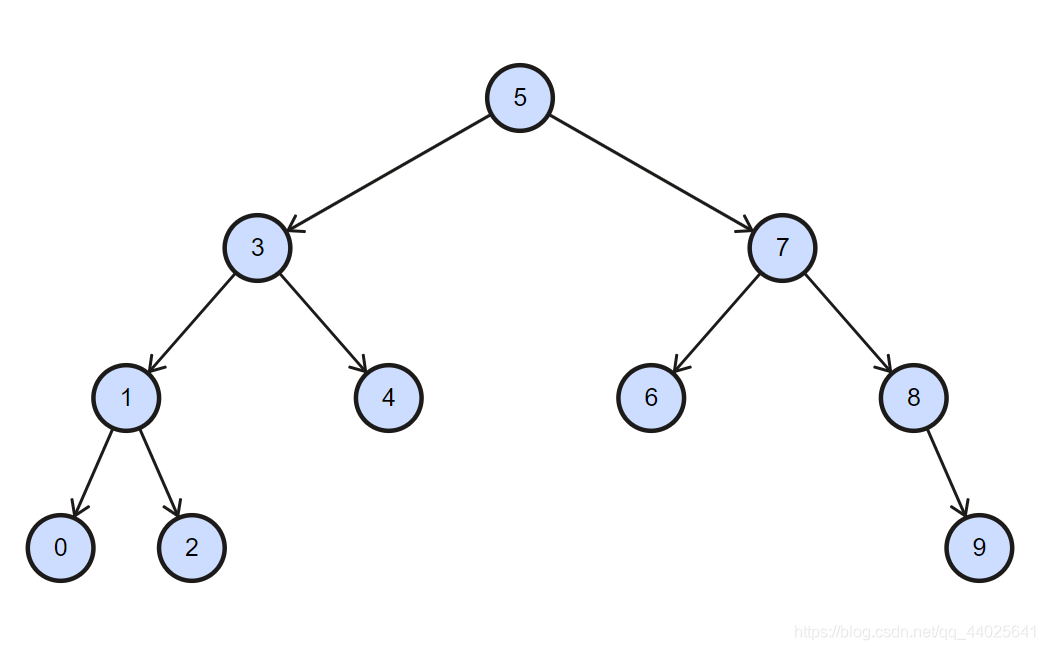
特點: 二叉搜索樹的中序遍歷結果是有序的(升序)!
實現一顆二叉搜索樹
- 實現二叉搜索樹,將實現插入,刪除,查找三個方面
- 二叉搜索樹的節點是不可以進行修改的,如果修改,則可能會導致搜索樹的錯誤
二叉搜索樹的定義類
- 二叉搜索樹的節點類 ——
class Node - 二叉搜索樹的屬性:要找到一顆二叉搜索樹隻需要知道這顆樹的根節點。
public class BST {
static class Node {
private int key;
private Node left;
private Node right;
public Node(int key) {
this.key = key;
}
}
private Node root;//BST的根節點
}
二叉搜索樹的查找
- 二叉搜索樹的查找思路:
- ①如果要查找的值等於當前節點的值,那麼,就找到瞭
- ②如果要查找的值小於當前節點的值,那麼,就往當前節點的左子樹走
- ③如果要查找的值大於當前節點的值,那麼,就往當前節點的右子樹走
- 最終,如果走到空瞭還沒有找到,就說明不存在這個
key
/**
* 查找是否存在節點
*
* 思路:根據二叉排序樹的特點:
* ①如果要查找的值小於當前節點的值,那麼,就往當前節點的左子樹走
* ②如果要查找的值大於當前節點的值,那麼,就往當前節點的右子樹走
*
* @param key 帶查找的key
* @return boolean是否存在
*/
public boolean find(int key) {
Node cur = root;
while (cur != null) {
if (key < root.key) {
cur = cur.left;
} else if (key > root.key) {
cur = cur.right;
} else {
return true;
}
}
return false;
}
二叉搜索樹的插入
- 二叉搜索樹的插入思路:
- 思路和查找一樣的,隻是我們這次要進行的是插入操作,那麼我們還需要一個
parent節點,來時刻記錄當前節點的雙親節點即: - ①如果要插入的值等於當前節點的值,那麼,無法插入(不可出現重復的
key) - ②如果要插入的值小於當前節點的值,那麼,就往當前節點的左子樹走
- ③如果要插入的值大於當前節點的值,那麼,就往當前節點的右子樹走
- 最終,如果走到空瞭,就說明不存在重復的
key,隻要往雙親節點的後面插就好瞭,就是合適的位置,具體往左邊還是右邊插入,需要比較待插入節點的key和parent的key
/**
* 往二叉樹中插入節點
*
* 思路如下:
*
* @param key 待插入的節點
*/
public void insert(int key) {
if (root == null) { //如果是空樹,那麼,直接插入
root = new Node(key);
return;
}
Node cur = root;
Node parent = null; //parent 為cur的父節點
while (true) {
if (cur == null) { //在遍歷過程中,找到瞭合適是位置,就指針插入(沒有重復節點)
if (parent.key < key) {
parent.right = new Node(key);
} else {
parent.left = new Node(key);
}
return;
}
if (key < cur.key) {
parent = cur;
cur = cur.left;
} else if (key > cur.key) {
parent = cur;
cur = cur.right;
} else {
throw new RuntimeException("插入失敗,已經存在key");
}
}
}
二叉搜索樹的刪除
- 二叉搜索樹的刪除思路:(詳細的思路看註釋)
- 首先,需要先找到是否存在
key節點,如果存在,則刪除,如果不存在則刪除錯誤 - 對於,如果存在,則分為三種情況:
- ①要刪除的節點,沒有左孩子
Ⅰ:要刪除的節點為根節點:root = delete.right;
Ⅱ:要刪除的節點為其雙親節點的左孩子:parent.left = delete.right;
Ⅲ:要刪除的節點為其雙親節點的右孩子:parent.right = delete.right;
- ②要刪除的節點,沒有右孩子
Ⅰ:要刪除的節點為根節點:root = delete.left;
Ⅱ:要刪除的節點為其雙親節點的左孩子:parent.left = delete.left;
Ⅲ:要刪除的節點為其雙親節點的右孩子:parent.right = delete.left;
- ③要刪除的節點,既有左孩子又有右孩子:
此時我們需要找到整顆二叉樹中第一個大於待刪除節點的節點,然後替換他倆的值,最後,把找到的節點刪除
Ⅰ:找到的節點的雙親節點為待刪除的節點:delete.key = find.key; findParent.right = find.right;
Ⅱ:找到的節點的雙親節點不是待刪除的節點:delete.key = find.key; findParent.left = find.right;
/**
* 刪除樹中節點
*
* 思路如下:
*
* @param key 待刪除的節點
*/
public void remove(int key) {
if (root == null) {
throw new RuntimeException("為空樹,刪除錯誤!");
}
Node cur = root;
Node parent = null;
//查找是否key節點的位置
while (cur != null) {
if (key < cur.key) {
parent = cur;
cur = cur.left;
} else if (key > cur.key) {
parent = cur;
cur = cur.right;
} else {
break;
}
}
if (cur == null) {
throw new RuntimeException("找不到key,輸入key不合法");
}
//cur 為待刪除的節點
//parent 為待刪除的節點的父節點
/*
* 情況1:如果待刪除的節點沒有左孩子
* 其中
* ①待刪除的節點有右孩子
* ②待刪除的節點沒有右孩子
* 兩種情況可以合並
*/
if (cur.left == null) {
if (cur == root) { //①如果要刪除的是根節點
root = cur.right;
} else if (cur == parent.left) { //②如果要刪除的是其父節點的左孩子
parent.left = cur.right;
} else { //③如果要刪除的節點為其父節點的右孩子
parent.right = cur.right;
}
}
/*
* 情況2:如果待刪除的節點沒有右孩子
*
* 其中:待刪除的節點必定存在左孩子
*/
else if (cur.right == null) { //①如果要刪除的是根節點
if (cur == root) {
root = cur.left;
} else if (cur == parent.left) { //②如果要刪除的是其父節點的左孩子
parent.left = cur.left;
} else { //③如果要刪除的節點為其父節點的右孩子
parent.right = cur.left;
}
}
/*
* 情況3:如果待刪除的節點既有左孩子又有右孩子
*
* 思路:
* 因為是排序二叉樹,要找到整顆二叉樹第一個大於該節點的節點,隻需要,先向右走一步,然後一路往最左走就可以找到瞭
* 因此:
* ①先向右走一步
* ②不斷向左走
* ③找到第一個大於待刪除的節點的節點,將該節點的值,替換到待刪除的節點
* ④刪除找到的這個節點
* ⑤完成刪除
*
*/
else {
Node nextParent = cur; //定義父節點,初始化就是待刪除的節點
Node next = cur.right; //定義next為當前走到的節點,最終目的是找到第一個大於待刪除的節點
while (next.left != null) {
nextParent = next;
next = next.left;
}
cur.key = next.key; //找到之後,完成值的替換
if (nextParent == cur) { //此時的父節點就是待刪除的節點,那麼說明找到的節點為父節點的右孩子(因為此時next隻走瞭一步)
nextParent.right = next.right;
} else { //此時父節點不是待刪除的節點,即next確實往左走瞭,且走到瞭頭.
nextParent.left = next.right;
}
}
}
到此這篇關於利用java實現二叉搜索樹的文章就介紹到這瞭,更多相關java二叉搜索樹內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!
推薦閱讀:
- None Found