python機器學習之線性回歸詳解
一、python機器學習–線性回歸
線性回歸是最簡單的機器學習模型,其形式簡單,易於實現,同時也是很多機器學習模型的基礎。
對於一個給定的訓練集數據,線性回歸的目的就是找到一個與這些數據最吻合的線性函數。

二、OLS線性回歸
2.1 Ordinary Least Squares 最小二乘法
一般情況下,線性回歸假設模型為下,其中w為模型參數
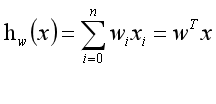
線性回歸模型通常使用MSE(均方誤差)作為損失函數,假設有m個樣本,均方損失函數為:(所有實例預測值與實際值誤差平方的均值)
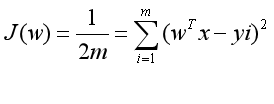
由於模型的訓練目標為找到使得損失函數最小化的w,經過一系列變換解得使損失函數達到最小值的w為:

此時求得的w即為最優模型參數
2.2 OLS線性回歸的代碼實現
#OLS線性回歸
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
%matplotlib inline
data = pd.DataFrame(pd.read_excel(r'C:/Users/15643/Desktop/附件1.xlsx'))
feature_data = data.drop(['企業信譽評估'],axis=1)
target_data = data['企業信譽評估']
X_train,X_test,y_train, y_test = train_test_split(feature_data, target_data, test_size=0.3)
from statsmodels.formula.api import ols
from statsmodels.sandbox.regression.predstd import wls_prediction_std
df_train = pd.concat([X_train,y_train],axis=1)
lr_model = ols("企業信譽評估~銷項季度均值+有效發票比例+是否違約+企業供求關系+行業信譽度+銷項季度標準差",data=df_train).fit()
print(lr_model.summary())
# 預測測試集
lr_model.predict(X_test)
三、梯度下降算法
很多機器學習算法的最優參數不能通過像最小二乘法那樣的“閉式”方程直接計算,此時需要使用迭代優化方法。
梯度學習算法可被描述為:
(1)根據當前參數w計算損失函數梯度∇J( w )
(2)沿著梯度反方向−∇J( w )調整w,調整的大小稱之為步長,由學習率η控制w:= w−η∇J( w )
(3)反復執行該過程,直到梯度為0或損失函數降低小於閾值,此時稱算法收斂。
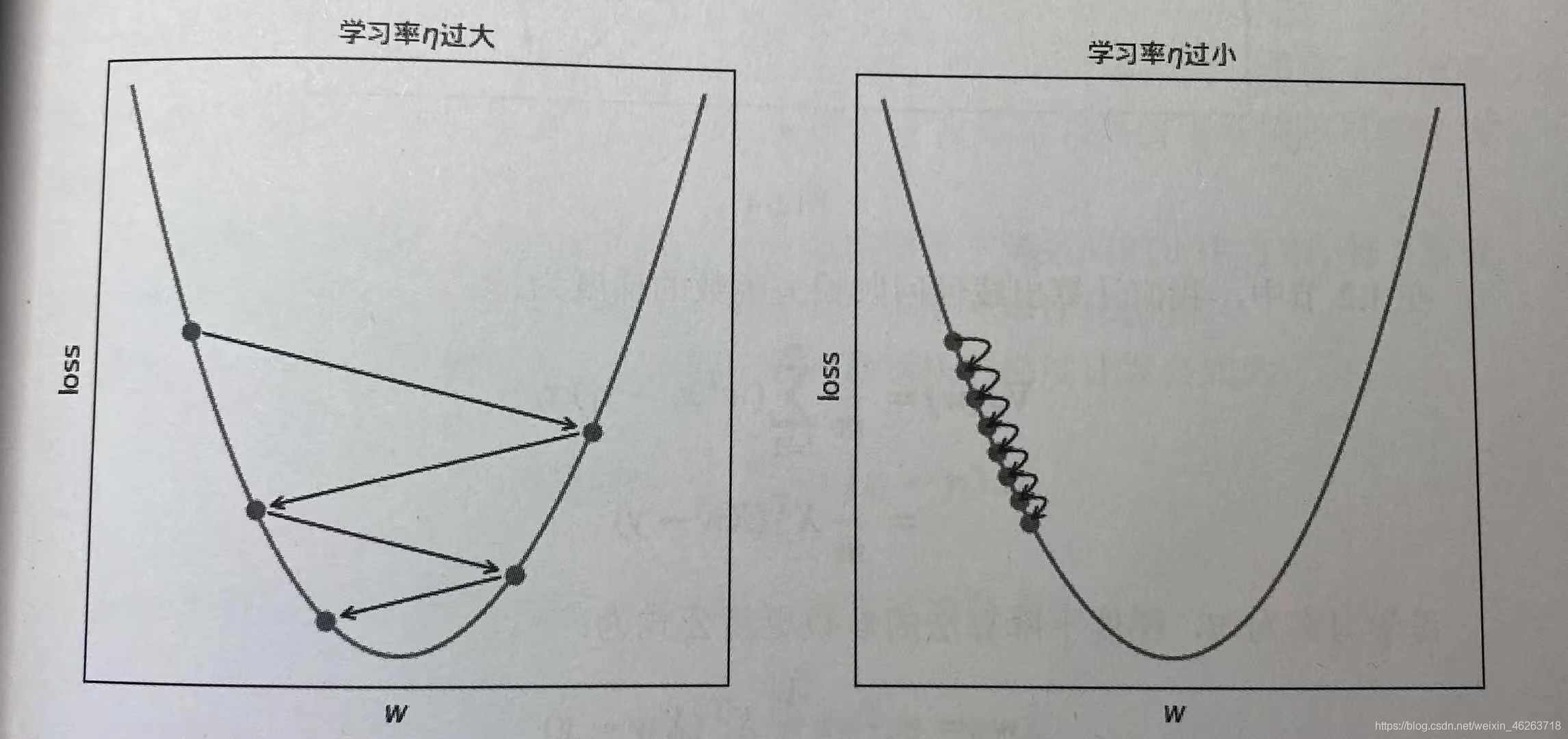
3.1 GDLinearRegression代碼實現
from linear_regression import GDLinearRegression gd_lr = GDLinearRegression(n_iter=3000,eta=0.001,tol=0.00001) #梯度下降最大迭代次數n_iter #學習率eta #損失降低閾值tol
四、多項式回歸分析
多項式回歸是研究一個因變量與一個或者多個自變量間多項式的回歸分析方法。
多項式回歸模型方程式如下:
hθ(x)=θ0+θ1x+θ2×2+…+θmxm
簡單來說就是在階數=k的情況下將每一個特征轉換為一個k階的多項式,這些多項式共同構成瞭一個矩陣,將這個矩陣看作一個特征,由此多項式回歸模型就轉變成瞭簡單的線性回歸。以下為特征x的多項式轉變:
x−>[1,x,x2,x3…xk]
4.1 多項式回歸的代碼實現
python的多項式回歸需要導入PolynomialFeatures類實現
#scikit-learn 多項式擬合(多元多項式回歸) #PolynomialFeatures和linear_model的組合 (線性擬合非線性) #[x1,x2,x3]==[[1,x1,x1**2],[1,x2,x2**2],[1,x3,x3**2]] import numpy as np import matplotlib.pyplot as plt from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression,Perceptron from sklearn.metrics import mean_squared_error,r2_score from sklearn.model_selection import train_test_split target = std_df_female['總分'] data_complete_ = std_df_female.loc[:,['1000/800','50m','立定跳遠','引仰']] x_train, x_test, y_train, y_test = train_test_split(data_complete_,target, test_size=0.3) # 多項式擬合 poly_reg =PolynomialFeatures(degree=2) x_train_poly = poly_reg.fit_transform(x_train) model = LinearRegression() model.fit(x_train_poly, y_train) #print(poly_reg.coef_,poly_reg.intercept_) #系數及常數 # 測試集比較 x_test_poly = poly_reg.fit_transform(x_test) y_test_pred = model.predict(x_test_poly) #mean_squared_error(y_true, y_pred) #均方誤差回歸損失,越小越好。 mse = np.sqrt(mean_squared_error(y_test, y_test_pred)) # r2 范圍[0,1],R2越接近1擬合越好。 r2 = r2_score(y_test, y_test_pred) print(r2)
到此這篇關於python機器學習之線性回歸詳解的文章就介紹到這瞭,更多相關python線性回歸內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!
推薦閱讀:
- None Found