R語言ARMA模型的參數選擇說明

Posted on by

AR(p)模型與MA(q)實際上是ARMA(p,q)模型的特例。它們都統稱為ARMA模型，而ARMA（p,q）模型的統計性質也是AR（p）與MA（q）模型的統計性質的有機組合。

平穩系列建模

假如某個觀察值序列通過序列預處理可以判定為平穩非白噪聲序列，就可以利用ARMA模型對序列建模。

1.求出該觀察值序列的樣本自相關系數（ACF）與偏相關系數（PACF的值。

2.根據根樣本自相關系數和偏自相關系數的性質，選擇階數適當的ARMA（p,q）模型進行擬合。

3.估計模型中未知參數的值

4.檢驗模型的有效性。如果擬合模型未通過檢驗，回到步驟（2）,重新選擇模型擬合。

5.模型優化。如果擬合模型通過檢驗，仍然回到步驟（2），充分考慮各種可能，建立多個擬合模型，從所有通過檢驗的擬合的模型中選擇最優模型。

6.利用擬合模型，預測序列將來的走勢。

選擇合適的模型擬合1950-2008年我國郵路及農村投遞線路每年新增裡程數序列：

白噪聲檢驗：

 for(i in 1:2) print(Box.test(x,type = "Ljung-Box",lag=6*i))
    Box-Ljung test
data:  x
X-squared = 37.754, df = 6, p-value = 1.255e-06
    Box-Ljung test
data:  x
X-squared = 44.62, df = 12, p-value = 1.197e-05

繪制自相關圖和偏自相關圖

acf(x)
pacf(x)

補充：關於ARMA模型的R語言實現

新手一枚，和大傢一起學習R，以後基本每周都會更新1到2篇關於數據預測處理的模型和方法，希望和大傢一起學習，一起成長。

本周首先更新的是用R來實現ARMA模型。

時間序列的模型，基本上都要建立在平穩的序列上，這裡我們將來瞭解下ARMA模型，以及其實現的R代碼。

ARMA（p,q)模型，全稱移動平均自回歸模型，它是由自回歸（AR）部分和移動平均（MA）部分組成的，所以稱之為ARMA模型。進行ARMA模型的話，要求時間序列一定要是平穩的才行，否則建模無效。

1.ARMA模型具有如下形式：

ARMA模型的基本定義

2.ARMA模型建模步驟

(1)畫出時序圖，求出樣本的相關系數，偏自相關系數值

(2)根據樣本的相關系數和偏自相關系數，選擇適當的階數，由於這具有一定的主觀性，所以這裡我們選用的是最小AIC準則來定階

(3)估計模型中的參數值

(4)檢驗模型的有效性，一般分為殘差的白噪聲檢驗和參數的顯著性檢驗。

(5)利用模型進行預測。

3.建模

我們利用美國科羅拉多州某一加油站連續57天的OVERSHOOT序列,來進行本次建模。

（1）首先

讀入數據，畫出其時序圖，檢驗其平穩性。

library(zoo)
library(tseries)
library(forecast)
overshort=read.table("C:/Users/MrDavid/data_TS/A1.9.csv",sep=",",header=T)
overshort=ts(overshort)
plot(overshort,col=4,lwd=2,pch=8,type="o")

結果如下：

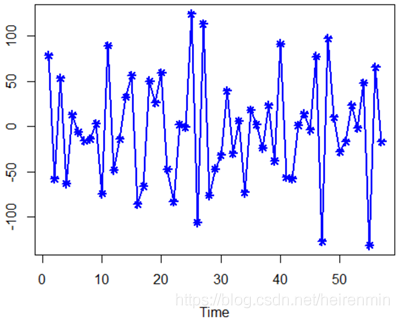
從這裡我們看到，這個時序圖應該是平穩的，但是為瞭以防萬一，我們進行單位根檢驗

進行一次單位根檢驗，測試該序列的平穩性：

代碼：adf.test(overshort)

結果如下圖所示：

單位根檢驗

由以上單位根檢驗，我們看到P值為0.01小於0.05，所以該序列平穩

（2）對於平穩的時間序列

我們需要進行白噪聲檢驗，因為白噪聲是純隨機序列，對白噪聲序列進行建模毫無意義。

for(i in 1:3) print(Box.test(overshort,type="Ljung-Box",lag=6*i))

結果如下圖：

一般我們進行白噪聲檢驗隻要檢驗到18到24項即可

可以看出，該序列非白噪聲序列，可以進行建模。

（3）模型的擬合

模型的擬合，我們可以畫出自相關圖，和偏自相關圖，對時間序列進行定階

acf(overshort,col=4,lwd=2)
pacf(overshort,col=4,lwd=2)

結果如下：

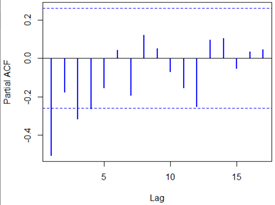
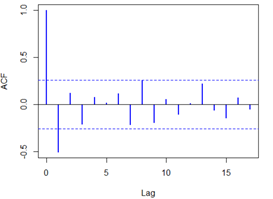
在這裡插入圖片描述在這裡插入圖片描述

自相關圖除瞭顯示1階延遲在兩倍標準差之外，其他自相關系數都在兩倍標準差之內，可以認為該序列自相關系數1階截尾，騙子相關系數顯示出非截尾性質，可以擬合模型為ARMA(0,1)，即MA(1)模型。

該模型除瞭自相關，偏自相關系數定階以外，還可以根據自動定階函數auto.arima來對該序列進行定階結果如下：

auto.arima(overshort)

在這裡插入圖片描述

也顯示出該序列的模型為MA(1)模型

接下來進行建模，找出模型的系數：

a=arima(overshort,order=c(0,0,1),include.mean=T)
a

得出結果：

在這裡插入圖片描述

該模型為：

在這裡插入圖片描述

對模型進行顯著性檢驗：

for(i in 1:3) print(Box.test(a$residual,type="Ljung-Box",lag=6*i))

在這裡插入圖片描述

殘差的白噪聲檢驗，反映出，該殘差是白噪聲序列，所以殘差白噪聲檢驗通過。

對參數進行顯著性檢驗：

t1=-0.8477/0.1206
pt(t1,df=12,lower.tail=T)
t2=-4.7945/1.0252
pt(t2,df=12,lower.tail=T)

在這裡插入圖片描述

參數的顯著性檢驗也通過，說明該序列建模成功。

（4）利用該模型預測未來5期值。

a.fore=forecast(a,h=5)
a.fore

在這裡插入圖片描述

（5）畫出預測圖：

L1=a.fore$fitted-1.96*sqrt(a$sigma2)
U1=a.fore$fitted+1.96*sqrt(a$sigma2)
L2=ts(a.fore$lower[,2])
U2=ts(a.fore$upper[,2])
c1=min(overshort,L1,L2)
c2=max(overshort,L2,U2)
plot(overshort,type="p",pch=8,ylim=c(c1,c2))
lines(a.fore$fitted,col=2,lwd=2)
lines(a.fore$mean,col=2,lwd=2)
lines(L1,col=4,lty=2)
lines(U1,col=4,lty=2)
lines(L2,col=4,lty=2)
lines(U2,col=4,lty=2)

以上為個人經驗，希望能給大傢一個參考，也希望大傢多多支持WalkonNet。如有錯誤或未考慮完全的地方，望不吝賜教。

推薦閱讀：

    None Found