Python數據結構與算法中的棧詳解(1)
什麼是棧
棧有時也被稱作“下推棧”。它是有序集合,添加操作和移除操作總發生在同一端,即棧的 “頂端”,棧的另一端則被稱為 “底端”。所以最新添加的元素將被最先移除,而且棧中的元素離底端越近,代表其在棧中的時間越長。
這種排序原則被稱作LIFO(last-in first-out),即後進先出。它提供瞭一種基於在集合中的時間來排序的方式。 最近添加的元素靠近頂端,舊元素則靠近底端。
棧的例子在日常生活中比比皆是。幾乎所有咖啡館都有一個由托盤或盤子構成的棧,你可以從頂部取走一個,下一 個顧客則會取走下面的托盤或盤子。
考慮到棧的反轉特性,我們可以想到在使用計算機時的一些例子。例如,每一個瀏覽器都有返回按鈕。當我們從一個網頁跳轉到另一個網頁時,這些網頁——實際上是URL,都被存放在一個棧中。當前正在瀏覽的網頁位於棧的頂端,最早瀏覽的網頁則位於底端。如果點擊返回按鈕, 便開始反向瀏覽這些網頁。
構建一個棧
如前所述,棧是元素的有序集合,添加操作與移除操作都發生在其頂端。棧的操作順序是LIFO,它支持以下操作:
- 將一個元素添加到棧的頂端
- 將棧頂端的元素移除
- 返回棧頂端的元素
- 返回棧中元素的數目
明確瞭棧的基本特性之後,我們開始用代碼構建它。在面向對象的編程語言中(以Python為例),每當需要在Python中實現像棧這樣的抽象數據類型時 ,就可以通過創建一個類的途徑實現它,且數據類型的特性、操作方法等也可以通過在類中定義方法實現。
我們來明確一下這個類的具體方法:
- 創建一個空棧。它不需要參數,且會返回一個空棧。 Stack()
- 將一個元素添加到棧的頂端。它需要一 個參數item ,且無返回值。 push(item)
- 將棧頂端的元素移除。它不需要參數,但會返回頂端的元素,並且修改棧的內容。 pop()
- 返回棧頂端的元素,但是並不移除該元素。 它不需要參數,也不會修改棧的內容。 peek()
- 返回棧中元素的數目。它不需要參數,且會返回一個整數。 size()
- 檢查棧是否為空。它不需要參數,且會返回一個佈爾值。 isEmpty()
- 打印這個棧/列表,它不需要參數,會輸出棧的內容。 look()
因為棧是元素的集合,所以完全可以利用Python提供的強大、簡單的原生集合來實現。這裡,我們將使用列表。 列表的最左端將用來表示棧底,最右邊將用來表示棧頂:
class Stack:
# 定義一個列表/構造一個棧
def __init__(self):
self.items = []
print("你創造瞭一個棧!")
def isEmpty(self):
return self.items == []
def look(self):
print(self.items)
def push(self, item):
self.items.append(item)
print("你給棧頂加瞭個%s" % item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items) - 1]
def size(self):
return len(self.items)
以下展示瞭棧的操作及其返回結果:
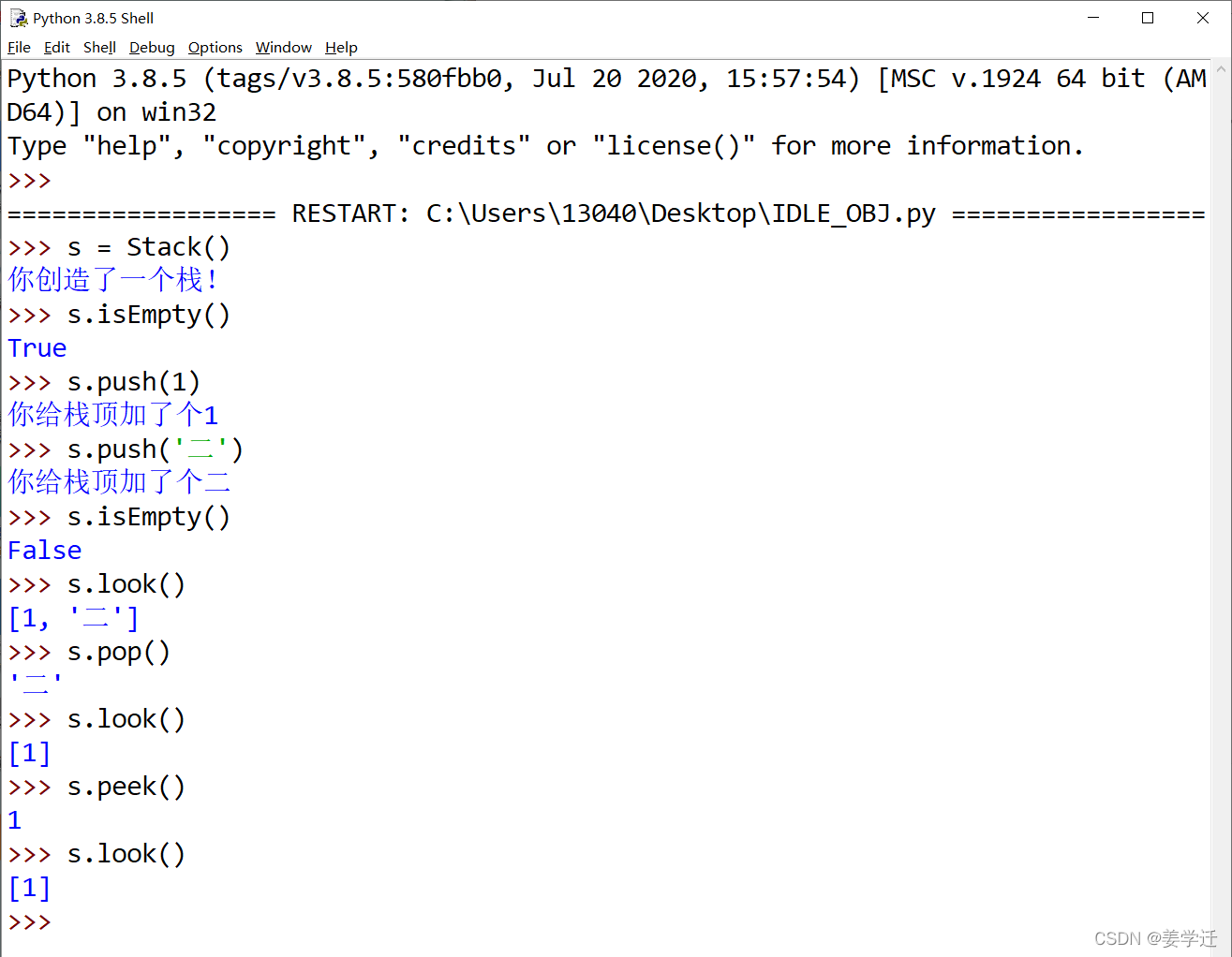
值得註意的是,也可以選擇將列表的頭部(左邊)作為棧的頂端。 不過在這種情況下,便無法直接使用列表的pop方法和append方法,而必須要用列表的pop方法和insert方法顯式地訪問下標為0的元素,即列表中的第1個元素。以下代碼展現瞭這種方式:
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def look(self):
print(self.items)
def push(self, item):
self.items.insert(0, item)
def pop(self):
return self.items.pop(0)
def peek(self):
return self.items[0]
def size(self):
return len(self.items)
盡管上述兩種實現都可行,但是二者在性能方面肯定有差異。append 方法和 pop 方法的時間復雜度都是 o ( 1 ) o(1) o(1),這意味著不論棧中有多少個元素, 第一種實現中的 push 操作和 pop 操作都會在恒定的時間內完成。第二種實現的性能則受制於棧中的元素個數,這 是因為 insert(0) 和 pop(0) 的時間復雜度都是 o ( n ) o(n) o(n),元素越多就越慢。
顯而易見,盡管兩種實現在邏輯上是相等的,但是它們在進行基準測試時耗費的時間會有很大的差異。
總結
本篇文章就到這裡瞭,希望能夠給你帶來幫助,也希望您能夠多多關註WalkonNet的更多內容!