C++高級數據結構之線段樹
前言:
- 高級數據結構(Ⅲ)線段樹(Segment Tree)
- 線段樹的原理
- 樹的創建
- 單點修改
- 區間查找
- 完整代碼及測試
高級數據結構(Ⅲ)線段樹(Segment Tree)
線段樹的原理
線段樹是一種二叉搜索樹 , 對於線段樹中的每一個非葉子結點[a,b],它的左兒子表示的區間為[a, (a+b)/2],右兒子表示的區間為[(a+b)/2+1, b]。因此線段樹是平衡二叉樹,最後的子節點數目為N,即整個線段區間的長度,其空間復雜度為O(n)。
若對於一個數組使用前綴和數組保存它的區間和,那麼查找區間和時間復雜度為O(1),而區間修改時間復雜度為O(n)。使用線段樹可以快速查找或修改某個區間的值,時間復雜度為O(logN)。
線段樹中每一個結點代表一個區間,對於區間【1, 7】線段樹的結構如下圖
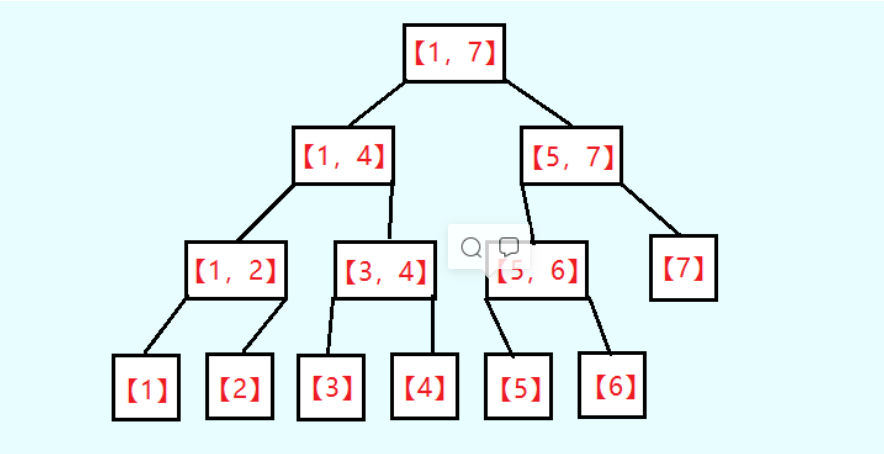
實例:
class SegmentTree{
private static final int[] tree = new int[1000];
int[] arr;
SegmentTree() {
}
SegmentTree(int[] arr) {
this.arr = arr;
}
//創建樹···
public void buildTree(){}
//單點修改更新樹
public void updateTree(){}
//區間查找
public void queryTree(){}
}
樹的創建
給定一個數組arr = [6, 4, 7, 5, 8, 3 , 9],創建它對應的線段樹數組。
對於一個結點k,它的左孩子為2 * k,右孩子為 2 * k + 1,此公式適用於根結點從1開始。但我們在數組中存儲元素時下標通常是從0開始的,即根結點從0開始,此時它的左孩子為 2 * k + 1, 右孩子為 2 * k + 2。
如下圖所示,數組arr的長度為7,由於樹是以2為基數的,且線段樹中葉子結點保存的是arr中單個結點的值,我們可以將數組arr的長度設想為8 (2 ^ 3 = 8,理解為新添瞭一個元素0,這對區間和並不影響),此時它對應的線段樹就是一棵結點數為15(1 + 2 + 4 + 8)的滿二叉樹。相應的結點值,映射到數組tree的值在圖中可清晰的看出。

那麼,如何用處程序來創建一棵樹呢?
由於線段樹葉子結點都是數組arr中的某一元素,所以我們可以使用兩個變量low和high來標記數組arr的區間,
- 若low == high,此時令tree[node] = arr[low],並終止遞歸
- 否則,將區間二分,分別計算左區間[low, mid]和右區間[mid +1, high],並在最後更新tree[node]
實現:
//創建樹
public void buildTree() {
this.buildTree(0, 0, arr.length - 1);
}
private void buildTree(int node, int low, int high) {
if(low == high) {
tree[node] = arr[low];
return;
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
buildTree(lnode, low, mid);
buildTree(rnode, mid + 1, high);
tree[node] = tree[lnode] + tree[rnode];
}
單點修改
若現在將arr[4]的值修改為1,需要怎樣操作呢?
從下圖綠色標出的結點不難看出其更新過程,先將其所對應的葉子結點修改,然後繼續向上修改其父節點即可。

當long==high&&low==index時更新兩個數組的值,否則,縮小區間,在相應的區間搜索,最後更新結點和即可,相應代碼如下
//單點修改更新樹
public void updateTree(int index, int val) {
this.updateTree(0, 0, arr.length - 1, index, val);
}
private void updateTree(int node, int low, int high, int index, int val) {
if(low == high && low == index) {
arr[index] = val;
tree[node] = val;
return;
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
if(index >= low && index <= mid) {
updateTree(lnode, low, mid, index, val);
}else {
updateTree(rnode, mid + 1, high, index, val);
}
tree[node] = tree[lnode] + tree[rnode];
}
區間查找
若現在查找數組arr區間和[3,6],如何利用線段樹呢?
在線段樹中,我們將它的和劃分為兩個區間[3]和[4,6],如圖中的黃色結點

下面來看看相關代碼如何實現,給定一個查找區間[L, R],同樣使用變量low和high維護對數組arr的二分查找邊界
- 若當前區間low > R 或者 high < L,說明已超出查找范圍,返回0
- 若[low, high]處於區間[L, R]內,返回當前結點的值tree[node]
然後繼續在左右區間查找並保存左右區間的值sumLeft和sumRight,最後返回sumLeft + sumRight即可
//區間查找
public int queryTree(int L, int R) {
return this.queryTree(0, 0, arr.length - 1, L, R);
}
private int queryTree(int node, int low,
int high, int L, int R) {
if(low > R || high < L) {
return 0;
}else if(low >= L && high <= R) {
return tree[node];
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
int sumleft = queryTree(lnode, low, mid, L, R);
int sumRight = queryTree(rnode, mid + 1, high, L, R);
return sumleft + sumRight;
}
完整代碼及測試
class SegmentTree{
private static final int[] tree = new int[1000];
int[] arr;
SegmentTree() {
}
SegmentTree(int[] arr) {
this.arr = arr;
}
//創建樹
public void buildTree() {
this.buildTree(0, 0, arr.length - 1);
}
private void buildTree(int node, int low, int high) {
if(low == high) {
tree[node] = arr[low];
return;
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
buildTree(lnode, low, mid);
buildTree(rnode, mid + 1, high);
tree[node] = tree[lnode] + tree[rnode];
}
//單點修改更新樹
public void updateTree(int index, int val) {
this.updateTree(0, 0, arr.length - 1, index, val);
}
private void updateTree(int node, int low, int high, int index, int val) {
if(low == high && low == index) {
arr[index] = val;
tree[node] = val;
return;
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
if(index >= low && index <= mid) {
updateTree(lnode, low, mid, index, val);
}else {
updateTree(rnode, mid + 1, high, index, val);
}
tree[node] = tree[lnode] + tree[rnode];
}
//區間查找
public int queryTree(int L, int R) {
return this.queryTree(0, 0, arr.length - 1, L, R);
}
private int queryTree(int node, int low, int high, int L, int R) {
if(low > R || high < L) {
return 0;
}else if(low >= L && high <= R) {
return tree[node];
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
int sumleft = queryTree(lnode, low, mid, L, R);
int sumRight = queryTree(rnode, mid + 1, high, L, R);
return sumleft + sumRight;
}
//輸出線段樹的值
public void printTree() {
int size = 15; //size值的大小由arr數組的大小而定
for (int i = 0; i < size; i++) {
System.out.print(tree[i] + " ");
}
System.out.println();
}
}
public class SegmentTreeTest {
public static void main(String[] args) {
int[] arr = {6, 4, 7, 5, 8, 3, 9};
SegmentTree st = new SegmentTree(arr);
//創建線段樹
st.buildTree();
st.printTree();
//>>>42 22 20 10 12 11 9 6 4 7 5 8 3 0 0
//查找區間[3, 6]
int sum = st.queryTree(3, 6);
System.out.println(sum);
//>>>25
//單點修改更新樹, 令arr[4] = 1
st.updateTree(4, 1);
st.printTree();
//>>>35 22 13 10 12 4 9 6 4 7 5 1 3 0 0
}
}
樹結點版本:
此版本不使用數組保存,而是以結點來保存值,相應代碼不難實現,如下:
import java.util.ArrayDeque;
import java.util.Deque;
class SegNode{
int val;
SegNode lnode;
SegNode rnode;
SegNode(){}
SegNode(int val) {
this.val = val;
}
}
class SegTree{
SegNode root;
int[] arr;
SegTree() {}
SegTree(int[] arr) {
this.arr = arr;
this.bulidTree();
}
//創建樹
public void bulidTree() {
root = this.buildTree(0, arr.length - 1);
}
private SegNode buildTree(int low, int high) {
if(low == high) {
return new SegNode(arr[low]);
}
SegNode node = new SegNode();
int mid = low + (high - low) / 2;
node.lnode = buildTree(low, mid);
node.rnode = buildTree(mid + 1, high);
node.val = node.lnode.val + node.rnode.val;
return node;
}
//單點修改更新樹
public void updateTree(int index, int val) {
root = updateTree(root ,0, arr.length - 1, index, val);
}
private SegNode updateTree(SegNode node, int low, int high, int index, int val) {
if(low == high && low == index) {
arr[index] = val;
node.val = val;
return node;
}
int mid = low + (high - low) / 2;
if(index >= low && index <= mid) {
node.lnode = updateTree(node.lnode, low, mid, index, val);
}else {
node.rnode = updateTree(node.rnode, mid + 1, high, index, val);
}
node.val = node.lnode.val + node.rnode.val;
return node;
}
//查找區間
public int queryTree(int L, int R) {
return queryTree(root, 0, arr.length - 1, L, R);
}
private int queryTree(SegNode node, int low, int high, int L ,int R) {
if(low > R || high < L) {
return 0;
}else if(low >= L && high <= R) {
return node.val;
}
int mid = low + (high - low) / 2;
int sumLeft = queryTree(node.lnode, low, mid, L, R);
int sumRight = queryTree(node.rnode, mid + 1, high, L, R);
return sumLeft + sumRight;
}
//輸出樹(層次遍歷)
public void printTree() {
Deque<SegNode> queue = new ArrayDeque<SegNode>();
queue.offer(this.root);
while(!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
SegNode node = queue.poll();
System.out.print(node.val + " ");
if(node.lnode != null) queue.offer(node.lnode);
if(node.rnode != null) queue.offer(node.rnode);
}
}
}
}
public class SegmentTreeNodeTest {
public static void main(String[] args) {
int[] arr = {6, 4, 7, 5, 8, 3, 9};
//創建線段樹
SegTree st = new SegTree(arr);
st.printTree();
System.out.println("");
//>>>42 22 20 10 12 11 9 6 4 7 5 8 3
//查找區間[3, 6]
int sum = st.queryTree(3, 6);
System.out.println(sum);
//>>>25
//單點修改更新樹, 令arr[4] = 1
st.updateTree(4, 1);
st.printTree();
System.out.println("");
>>>35 22 13 10 12 4 9 6 4 7 5 1 3
}
}
到此這篇關於C++高級數據結構之線段樹的文章就介紹到這瞭,更多相關C++線段樹內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!