Python使用scipy.fft進行大學經典的傅立葉變換

Posted on by

傅裡葉變換是在高數是一個很重要的知識點，今天將結合Python代碼實現傅立葉變換。

傅立葉變換

我們平時是如何去分解一個復雜的問題呢？一個經典的方法就是把這個復雜的問題分解成為多個簡單的可操作的子問題， 傅立葉變換也是基於這個思想。

傅裡葉分析是研究如何將數學函數分解為一系列更簡單的三角函數的領域。傅裡葉變換是該領域的一種工具，用於將函數分解為其分量頻率。

在本教程中，傅立葉變換是一種工具，可以獲取信號並查看其中每個頻率的功率。看一看該傅立葉變換中的重要術語：

  • 信號：信號是隨時間變化的信息。例如，音頻，視頻和電壓走線都是信號的示例。
  • 頻率：頻率是某物重復的速度。例如，時鐘以1赫茲（Hz）的頻率滴答，或每秒重復1次。
  • 功率：功率表示每個頻率的強度。

下圖是一些正弦波的頻率和功率的直觀演示：

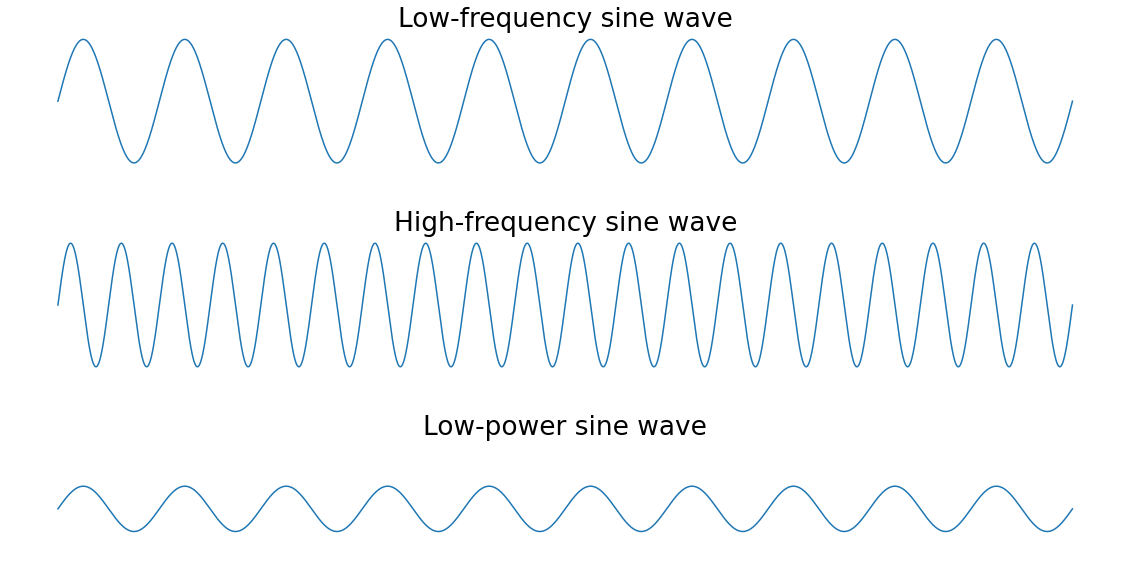
第一個是低頻正弦波，第二個是高頻正弦波，第三個是低頻低功率正弦波，因此低功率正弦波比其它兩個正弦波的峰較小。

時域與頻域

時域與頻域是查看信號的兩種不同方式，即信號的組成頻率或隨時間變化的信息。

在時域中，信號是隨時間（x軸）幅度（y軸）變化的波。您最有可能在時域中查看圖表，例如：

這是一些音頻的圖像，它是一個時域信號。橫軸表示時間，縱軸表示振幅。

在頻域中，信號表示為一系列頻率（x軸），每個頻率都具有關聯的功率（y軸）。下圖是經過傅立葉變換後的上述音頻信號：

代碼實現正弦波

音頻本質上是正弦波。

下面是產生正弦波的代碼：

import numpy as np
from matplotlib import pyplot as plt

SAMPLE_RATE = 44100  # 赫茲
DURATION = 5  # 秒

def generate_sine_wave(freq, sample_rate, duration):
    x = np.linspace(0, duration, sample_rate * duration, endpoint=False)
    frequencies = x * freq
   
    y = np.sin((2 * np.pi) * frequencies)
    return x, y

# 產生持續5秒的2赫茲正弦波
x, y = generate_sine_wave(2, SAMPLE_RATE, DURATION)
plt.plot(x, y)
plt.show()

在這裡插入圖片描述

x軸以秒為單位表示時間，並且由於每秒鐘的時間都有兩個峰值，因此可以看到正弦波每秒振蕩兩次。

混合音頻

下面將兩個正弦波，混合音頻信號僅包括兩個步驟：

將正弦波加在一起，然後進行歸一化的操作。

具體實現的代碼如下。

_, nice_tone = generate_sine_wave(400, SAMPLE_RATE, DURATION)
_, noise_tone = generate_sine_wave(4000, SAMPLE_RATE, DURATION)
noise_tone = noise_tone * 0.3

mixed_tone = nice_tone + noise_tone

下一步是歸一化，或縮放信號以適合目標格式。由於以後將如何存儲音頻，目標格式為16位整數，范圍為-32768到32767：

normalized_tone = np.int16((mixed_tone / mixed_tone.max()) * 32767)

plt.plot(normalized_tone[:1000])
plt.show()

在這裡插入圖片描述

看到的正弦波是生成的400 Hz音調，將上面的正弦波轉化為音頻，最簡單的方法是使用SciPy的wavfile.write方法將其存儲在WAV文件中。16位整數是WAV文件的標準數據類型，因此需要將信號標準化為16位整數：

from scipy.io.wavfile import write

# 記住，采樣率=44100赫茲是我們的播放率
write("mysinewave.wav", SAMPLE_RATE, normalized_tone)

這個音頻聽起來音調很高。

完成此步驟後，就當作音頻樣本瞭。下一步是使用傅立葉變換消除高音調！

傅立葉變換

現在對生成的音頻上使用FFT瞭。FFT是一種算法，可實現傅立葉變換並可以在時域中為信號計算頻譜。

from scipy.fft import fft, fftfreq

# 標準化音調中的樣本數
N = SAMPLE_RATE * DURATION

yf = fft(normalized_tone)
xf = fftfreq(N, 1 / SAMPLE_RATE)

plt.plot(xf, np.abs(yf))
plt.show()


我們可以在正頻率中看到兩個峰值，正頻率峰值位於400 Hz和4000 Hz，與之前生成的音頻的頻率相對應。

計算傅裡葉變換

yf = fft(normalized_tone)
xf = fftfreq(N, 1 / SAMPLE_RATE)

上面代碼的功能

  • fft() 計算轉換本身。
  • fftfreq()計算的輸出中每個倉中心的頻率fft()。沒有這個，就無法在頻譜上繪制x軸

fft()輸出的頻譜圍繞y軸反射，因此負半部分是正半部分的鏡像，我們一般隻需計算一半對稱值，即可更快地進行傅立葉變換。scipy.fft以的形式實施此速度駭客rfft()。

from scipy.fft import rfft, rfftfreq

# 註意前面多餘的“r”
yf = rfft(normalized_tone)
xf = rfftfreq(N, 1 / SAMPLE_RATE)

plt.plot(xf, np.abs(yf))
plt.show()

過濾信號

傅裡葉變換的一大優點是它是可逆的，我們可以利用此優勢來過濾音頻並擺脫高音調頻率。

# 最大頻率為采樣率的一半
points_per_freq = len(xf) / (SAMPLE_RATE / 2)

# 我們的目標頻率是4000赫茲 將44100變成4000
target_idx = int(points_per_freq * 4000)

然後，您可以將其設置yf為0目標頻率附近的index來擺脫它：

yf[target_idx - 1 : target_idx + 2] = 0

plt.plot(xf, np.abs(yf))
plt.show()

在這裡插入圖片描述

由於隻有一個高峰，下面應用傅立葉逆變換返回時域。

應用逆FFT與應用FFT相似：

from scipy.fft import irfft

new_sig = irfft(yf)

plt.plot(new_sig[:1000])
plt.show()

由於您正在使用rfft()，因此需要使用irfft()來應用反函數。但是，如果您使用過fft()，則反函數將是ifft()。現在，您的繪圖應如下所示：

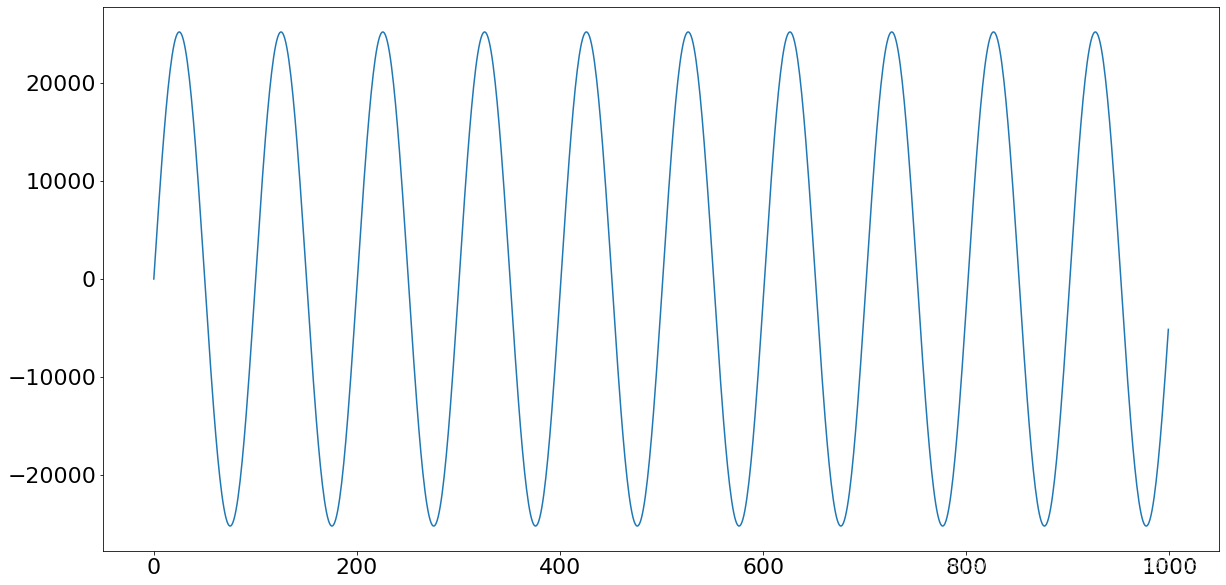
現在有一個以400 Hz振蕩的正弦波，並且您已經成功地消除瞭4000 Hz的噪聲。

對信號進行歸一化，然後再將其寫入文件。

norm_new_sig = np.int16(new_sig * (32767 / new_sig.max()))

write("clean.wav", SAMPLE_RATE, norm_new_sig)

在這裡插入圖片描述

到此這篇關於Python使用scipy.fft進行大學經典的傅立葉變換的文章就介紹到這瞭,更多相關Python 傅立葉變換內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet！

推薦閱讀：