Python實現CART決策樹算法及詳細註釋

Posted on by

一、CART決策樹算法簡介

CART（Classification And Regression Trees 分類回歸樹）算法是一種樹構建算法，既可以用於分類任務，又可以用於回歸。相比於 ID3 和 C4.5 隻能用於離散型數據且隻能用於分類任務，CART 算法的適用面要廣得多，既可用於離散型數據，又可以處理連續型數據，並且分類和回歸任務都能處理。

本文僅討論基本的CART分類決策樹構建，不討論回歸樹和剪枝等問題。

首先，我們要明確以下幾點：
1. CART算法是二分類常用的方法，由CART算法生成的決策樹是二叉樹，而 ID3 以及 C4.5 算法生成的決策樹是多叉樹，從運行效率角度考慮，二叉樹模型會比多叉樹運算效率高。
2. CART算法通過基尼(Gini)指數來選擇最優特征。

二、基尼系數

基尼系數代表模型的不純度，基尼系數越小，則不純度越低，註意這和 C4.5的信息增益比的定義恰好相反。

分類問題中，假設有K個類，樣本點屬於第k類的概率為pk，則概率分佈的基尼系數定義為:

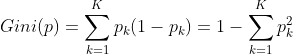
在這裡插入圖片描述

若CART用於二類分類問題（不是隻能用於二分類），那麼概率分佈的基尼系數可簡化為

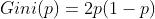
在這裡插入圖片描述

假設使用特征 A 將數據集 D 劃分為兩部分 D1 和 D2，此時按照特征 A 劃分的數據集的基尼系數為：

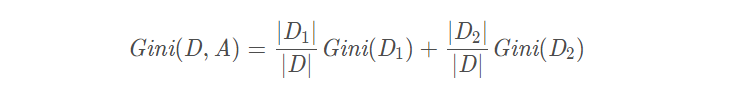
在這裡插入圖片描述

三、CART決策樹生成算法

輸入：訓練數據集D，停止計算的條件
輸出：CART決策樹
根據訓練數據集，從根結點開始，遞歸地對每個結點進行以下操作，構建二叉決策樹：
（1）計算現有特征對該數據集的基尼指數，如上面所示；
（2）選擇基尼指數最小的值對應的特征為最優特征，對應的切分點為最優切分點（若最小值對應的特征或切分點有多個，隨便取一個即可）；
（3）按照最優特征和最優切分點，從現結點生成兩個子結點，將訓練數據集中的數據按特征和屬性分配到兩個子結點中；
（4）對兩個子結點遞歸地調用（1）（2）（3），直至滿足停止條件。
（5）生成CART樹。
算法停止的條件：結點中的樣本個數小於預定閾值，或樣本集的基尼指數小於預定閾值（樣本基本屬於同一類，如完全屬於同一類則為0），或者特征集為空。
註：最優切分點是將當前樣本下分為兩類（因為我們要構造二叉樹）的必要條件。對於離散的情況，最優切分點是當前最優特征的某個取值；對於連續的情況，最優切分點可以是某個具體的數值。具體應用時需要遍歷所有可能的最優切分點取值去找到我們需要的最優切分點。

四、CART算法的Python實現

若是二分類問題，則函數calcGini和choose_best_feature可簡化如下：

# 計算樣本屬於第1個類的概率p
def calcProbabilityEnt(dataset):
    numEntries = len(dataset)
    count = 0
    label = dataset[0][len(dataset[0]) - 1]
    for example in dataset:
        if example[-1] == label:
            count += 1
    probabilityEnt = float(count) / numEntries
    return probabilityEnt

def choose_best_feature(dataset):
    # 特征總數
    numFeatures = len(dataset[0]) - 1
    # 當隻有一個特征時
    if numFeatures == 1:
        return 0
    # 初始化最佳基尼系數
    bestGini = 1
    # 初始化最優特征
    index_of_best_feature = -1
    for i in range(numFeatures):
        # 去重，每個屬性值唯一
        uniqueVals = set(example[i] for example in dataset)
        # 定義特征的值的基尼系數
        Gini = {}
        for value in uniqueVals:
            sub_dataset1, sub_dataset2 = split_dataset(dataset,i,value)
            prob1 = len(sub_dataset1) / float(len(dataset))
            prob2 = len(sub_dataset2) / float(len(dataset))
            probabilityEnt1 = calcProbabilityEnt(sub_dataset1)
            probabilityEnt2 = calcProbabilityEnt(sub_dataset2)
            Gini[value] = prob1 * 2 * probabilityEnt1 * (1 - probabilityEnt1) + prob2 * 2 * probabilityEnt2 * (1 - probabilityEnt2)
            if Gini[value] < bestGini:
                bestGini = Gini[value]
                index_of_best_feature = i
                best_split_point = value
    return index_of_best_feature, best_split_point

五、運行結果

在這裡插入圖片描述

到此這篇關於Python實現CART決策樹算法及詳細註釋的文章就介紹到這瞭,更多相關Python策樹算法內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet！

推薦閱讀：