人工智能-Python實現嶺回歸

Posted on by

1 概述

1.1 線性回歸

對於一般地線性回歸問題，參數的求解采用的是最小二乘法，其目標函數如下：

argmin\left \| Xw-y \right \|^{2}

參數 w 的求解，也可以使用如下矩陣方法進行：

w=(X^{T}X)^{-1}X^{T}y

這個公式看著嚇人，其實推導過程簡單由（y=wX推導而來，紙老虎）
對於矩陣 X ，若某些列線性相關性較大（即訓練樣本中某些屬性線性相關），就會導致
的值接近 0 ，在計算\left ( X^{T}X\right )^{-1}時就會出現不穩定性。
結論 ： 傳統的基於最小二乘的線性回歸法缺乏穩定性。

1.2 嶺回歸 

嶺回歸的優化目標：

argmin\left \| Xw-y \right \|^{2}+\partial \left \| w \right \|^{2}

 對應的矩陣求解方法為：                

w=(X^{T}X+\partial I)^{-1}X^{T}y

嶺回歸(ridge regression) 是一種專用於共線性數據分析的有偏估計回歸方法。
是一種改良的最小二乘估計法，對某些數據的擬合要強於最小二乘法。

1.3 過擬合

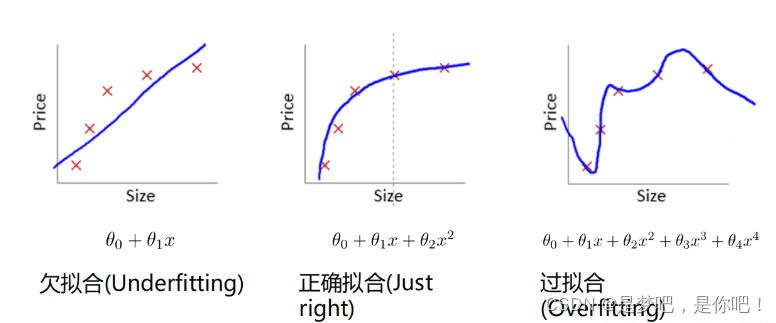
圖二就是正常擬合，符合數據的趨勢，而圖三，雖然在訓練集上擬合得很好，但是出現未知數據時，比如Size很大時，根據目前擬合來看，可能得到的結果很小，與實際誤差會很大。 

2 sklearn中的嶺回歸

在sklearn庫中，可以使用sklearn.linear_model.Ridge調用嶺回歸模型，其主要參數有：

• alpha：正則化因子，對應於損失函數中的 𝜶
• fit_intercept：表示是否計算截距，
• solver：設置計算參數的方法，可選參數‘auto’、‘svd’、‘sag’等。

3 案例 

交通流量預測實例：

3.1 數據介紹

數據為某路口的交通流量監測數據，記錄全年小時級別的車流量。

3.2 實驗目的

根據已有的數據創建多項式特征，使用嶺回歸模型代替一般的線性模型，對 車流量 的信息進行 多項式回歸 。

3.3 數據特征如下

HR ：一天中的第幾個小時（0-23）
WEEK_DAY ：一周中的第幾天（0-6）
DAY_OF_YEAR ：一年中的第幾天（1-365）
WEEK_OF_YEAR ：一年中的第幾周（1-53）
TRAFFIC_COUNT ：交通流量
全部數據集包含2萬條以上數據（21626）

4 Python實現 

4.1 代碼

#*================1. 建立工程，導入sklearn相關工具包====================**
import numpy as np
from sklearn.linear_model import Ridge   #通過sklearn.linermodel加載嶺回歸方法
from sklearn import model_selection     #加載交叉驗證模塊
import matplotlib.pyplot as plt      #加載matplotilib模塊
from sklearn.preprocessing import PolynomialFeatures     #通過加載用於創建多項式特征，如ab、a2、b2
 
#*=================2. 數據加載=========================================**
data=np.genfromtxt('嶺回歸.csv',delimiter=',')     #使用numpy的方法從csv文件中加載數據
print(data)
print(data.shape)
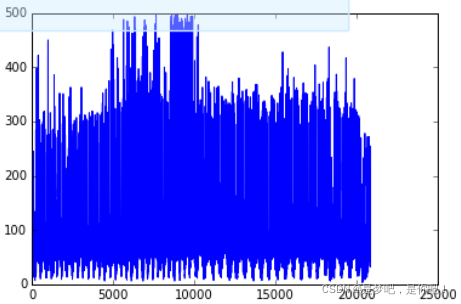
plt.plot(data[:,4])                #使用plt展示車流量信息
#plt.show()
#*================3. 數據處理==========================================**
X=data[:,:4]                  #X用於保存0-3維數據，即屬性
y=data[:,4]                   ##y用於保存第4維數據，即車流量
poly=PolynomialFeatures(6)    #用於創建最高次數6次方的的多項式特征，多次試驗後決定采用6次
X=poly.fit_transform(X)       #X為創建的多項式特征
 
#*================4. 劃分訓練集和測試集=================================**
train_set_x, test_set_x , train_set_y, test_set_y =model_selection.train_test_split(X,y,test_size=0.3,
random_state=0)
#將所有數據劃分為訓練集和測試集，test_size表示測試集的比例，
# #random_state是隨機數種子
 
#*==============5. 創建回歸器，並進行訓練===============================**
clf=Ridge(alpha=1.0,fit_intercept = True)
#接下來我們創建嶺回歸實例
clf.fit(train_set_x,train_set_y) #調用fit函數使用訓練集訓練回歸器
clf.score(test_set_x,test_set_y) #利用測試集計算回歸曲線的擬合優度，clf.score返回值為0.7375
#擬合優度，用於評價擬合好壞，最大為1，無最小值，當對所有輸入都輸出同一個值時，擬合優度為0。
 
#*============6. 畫出擬合曲線=========================================**
start=100                      #接下來我們畫一段200到300范圍內的擬合曲線
end=200
y_pre=clf.predict(X)           #是調用predict函數的擬合值
time=np.arange(start,end)
plt.plot(time,y[start:end],'b', label="real")
plt.plot(time,y_pre[start:end],'r', label='predict')   #展示真實數據（藍色）以及擬合的曲線（紅色）
plt.legend(loc='upper left') #設置圖例的位置
plt.show()

4.2 結果 

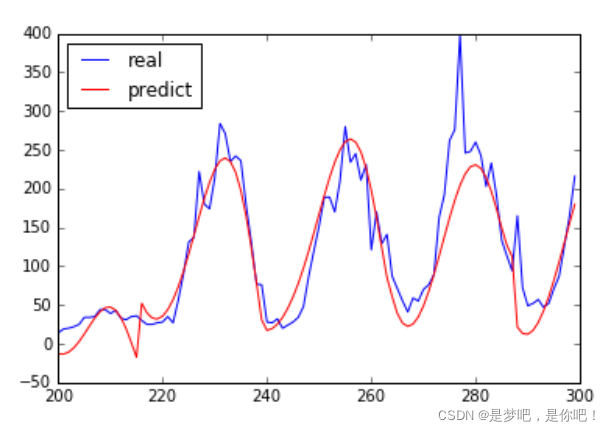
分析結論 ：預測值和實際值的走勢大致相同

到此這篇關於人工智能-Python實現嶺回歸的文章就介紹到這瞭,更多相關Python實現嶺回歸內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet！

推薦閱讀：