運籌學-Python實現圖論與最短距離
1 概述
1.1 貪心算法
貪心算法總是作出在當前看來最好的選擇。也就是說貪心算法並不從整體最優考慮,它所作出的選擇隻是在某種意義上的局部最優選擇。當然,希望貪心算法得到的最終結果也是整體最優的。雖然貪心算法不能對所有問題都得到整體最優解,但對許多問題它能產生整體最優解。如單源最短路經問題,最小生成樹問題等。在一些情況下,即使貪心算法不能得到整體最優解,其最終結果卻是最優解的很好近似。
基本思路:從問題的某一個初始解出發逐步逼近給定的目標,以盡可能快的地求得更好的解。當達到算法中的某一步不能再繼續前進時,算法停止。
該算法存在問題:
- (1)不能保證求得的最後解是最佳的;
- (2)不能用來求最大或最小解問題;
- (3)隻能求滿足某些約束條件的可行解的范圍。
實現該算法的偽代碼:
從問題的某一初始解出發;
while 能朝給定總目標前進一步 do
求出可行解的一個解元素由所有解元素組合成問題的一個可行解;
1.2 圖論及求解最短距離
1.2.1 方法選擇
- (1)需要求解任意兩個節點之間的最短距離,使用 Floyd 算法;
- (2)隻要求解單源最短路徑問題,有負權邊時使用 Bellman-Ford 算法,沒有負權邊時使用 Dijkstra 算法;
- (3)A*算法找到的是相對最優路徑,適合大規模、實時性高的問題。
本節我們隻討論Dijkstra 算法。
1.2.2 狄克斯屈拉(Dijkstra)算法
適用於wij≥0,給出瞭從vs到任意一個點vj的最短路。
Dijkstra算法是在1959年提出來的。目前公認,在所有的權wij ≥0時,這個算法是尋求最短路問題最好的算法。並且,這個算法實際
上也給出瞭尋求從一個始定點vs到任意一個點vj的最短路。
2 案例1——貪心算法實現
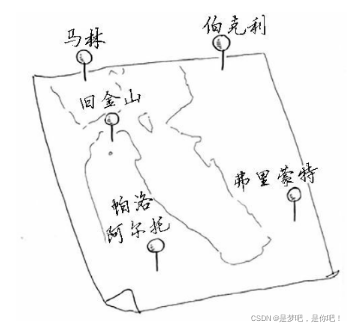
2.1 旅行商問題(TSP)
旅行商問題(TravelingSalesmanProblem,TSP)一個商品推銷員要去若幹個城市推銷商品,該推銷員從一個城市出發,需要遍歷所有城市一次且隻能一次,回到出發地。應如何選擇行進路線,以使總的行程最短。
旅行商問題(TSP)即給定一組城市以及每對城市之間的距離,需要找到一條最短的路線,該路線隻對每個城市進行一次訪問並返回起點。
這裡註意漢密爾頓活路(Hamiltonian Cycle)和TSP之間的區別。漢密爾頓回路問題是要找出是否存在一次遊覽每個城市一次的路線。在TSP問題中,我們是已知存在漢密爾頓回路(因為該圖是完整的),並且實際上,存在許多此類回路,TSP問題在於找到最小權重的漢密爾頓回路。
目前解決TSP問題的方法有許多種,比如:貪心算法、動態規劃算法、分支限界法;也有智能算法。本文先介紹貪心算法:
2.2 案例
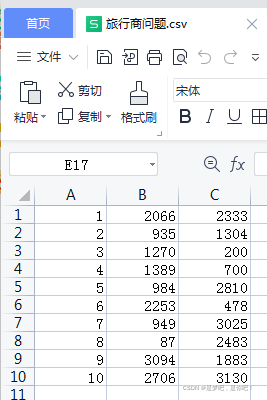
數據 如下圖,第一列城市名。第二列坐標x,第三列坐標y:
貪心算法思路:隨便選擇出發城市,然後每次選擇要去的下一個城市時,都選擇還沒去的最近的城市。
2.3 Python實現
#========第一步:導入相關庫==================
import pandas as pd
import numpy as np
import math
import time
#======第二步:讀取數據=================
dataframe = pd.read_csv("旅行商問題.csv", sep=",", header=None)
v = dataframe.iloc[:, 1:3] #去除第一列12345678910,隻保留x,y
print('讀取數據:----------------------------')
print(v)
#=======第三步:計算城市之間的距離========
train_v= np.array(v)
train_d=train_v
dist = np.zeros((train_v.shape[0],train_d.shape[0])) #初始化距離 為10*10的全0矩陣
print(dist.shape) #(10,10)
#==計算距離矩陣===
for i in range(train_v.shape[0]):
for j in range(train_d.shape[0]):
dist[i,j] = math.sqrt(np.sum((train_v[i,:]-train_d[j,:])**2))
print('距離矩陣:----------------------------------')
print(dist)
#==========第四步:計算距離和路徑==============
"""
s:已經遍歷過的城市
dist:城市間距離矩陣
sumpath:目前的最小路徑總長度
Dtemp:當前最小距離
flag:訪問標記
"""
i=1
n=train_v.shape[0]#城市個數
j=0
sumpath=0#目前的最小路徑總長度
s=[]#已經遍歷過的城市
s.append(0)#從城市0開始
start = time.perf_counter() #time.clock()
while True:
k=1#從1開始,因為人在城市0,所以我們設定先從城市1開始選擇
Detemp=float('inf')#當前最小距離
while True:
flag=0#訪問標記,否0
if k in s:#是否訪問,如果訪問過,flag設為1
flag = 1
if (flag==0) and (dist[k][s[i-1]] < Detemp):#如果未訪問過,並且距離小於最小距離
j = k;
Detemp=dist[k][s[i - 1]]; #當前兩座城市相鄰距離
k+=1#遍歷下一城市
if k>=n:
break;
s.append(j)
i+=1;
sumpath+=Detemp
if i>=n:
break;
sumpath+=dist[0][j]#加上dist[0][j] 表示最後又回到起點
end = time.perf_counter() #time.clock()
print("距離:")
print(sumpath)
print('*--------------*')
print('路徑:')
for m in range(n):
print("%s-> "%(s[m]),end='')
print()
print("程序的運行時間是:%s"%(end-start))
代碼解析:數字k表示當前我們選擇前往下一個城市時,我們需要計算所有未訪問過的城市和當前城市距離。
數字i 用於控制訪問過的城市,我們需要到達每一個城市。
代碼中有兩個while
裡面那個while表示選擇下一城市時,需要遍歷所有未訪問過的城市,然後選擇距離當前城市最近的城市,賦值給j
外面while,表示我們的每一步,我們需要去每個城市。
2.4 結果
讀取數據:
1 2
0 2066 2333
1 935 1304
2 1270 200
3 1389 700
4 984 2810
5 2253 478
6 949 3025
7 87 2483
8 3094 1883
9 2706 3130
(10, 10)
距離矩陣:———————————-
[[ 0. 1529.05264788 2276.68728639 1767.77204413 1182.47748393
1864.40178073 1313.98363765 1984.67654795 1122.17823896 1022.15898959]
[1529.05264788 0. 1153.70750193 755.6004235 1506.7969339
1555.44205935 1721.0569427 1452.28957168 2235.29013777 2543.76040538]
[2276.68728639 1153.70750193 0. 513.96595218 2625.6229737
1021.55420806 2843.17885473 2571.29889356 2481.82694804 3262.97349055]
[1767.77204413 755.6004235 513.96595218 0. 2148.51693035
892.06502005 2366.26815894 2207.7801068 2075.21420581 2763.94446399]
[1182.47748393 1506.7969339 2625.6229737 2148.51693035 0.
2654.91713618 217.83020911 954.74499213 2304.65377009 1751.48051659]
[1864.40178073 1555.44205935 1021.55420806 892.06502005 2654.91713618
0. 2861.40262808 2951.53875123 1637.46938903 2690.41130685]
[1313.98363765 1721.0569427 2843.17885473 2366.26815894 217.83020911
2861.40262808 0. 1018.23769327 2430.05946429 1760.13465394]
[1984.67654795 1452.28957168 2571.29889356 2207.7801068 954.74499213
2951.53875123 1018.23769327 0. 3066.2760802 2697.7342345 ]
[1122.17823896 2235.29013777 2481.82694804 2075.21420581 2304.65377009
1637.46938903 2430.05946429 3066.2760802 0. 1305.9682232 ]
[1022.15898959 2543.76040538 3262.97349055 2763.94446399 1751.48051659
2690.41130685 1760.13465394 2697.7342345 1305.9682232 0. ]]
距離:
10464.183486532447
*————–*
路徑:
0-> 9-> 8-> 5-> 3-> 2-> 1-> 7-> 4-> 6->
程序的運行時間是:0.0002605780000024538
Process finished with exit code 0
3 案例2——圖論及最短距離
3.1 知識點

3.2 networkx繪圖
3.2.1 創建圖
networkx有四種圖 Graph 、DiGraph、MultiGraph、MultiDiGraph,分別為無多重邊無向圖、無多重邊有向圖、有多重邊無向圖、有多重邊有向圖。
#==========創建圖================ import networkx as nx # 導入 NetworkX 工具包 G1 = nx.Graph() # 創建:空的 無向圖 G2 = nx.DiGraph() #創建:空的 有向圖 G3 = nx.MultiGraph() #創建:空的 多圖 G4 = nx.MultiDiGraph() #創建:空的 有向多圖
3.2.2 定點的添加、刪除和查看
#================頂點的添加、刪除和查看=============
#======頂點(node)的操作=====
#==向圖中添加頂點==
G1.add_node(1) # 向 G1 添加頂點 1
G1.add_node(1, name='n1', weight=1.0) # 添加頂點 1,定義 name, weight 屬性
G1.add_node(2, date='May-16') # 添加頂點 2,定義 time 屬性
G1.add_nodes_from([3, 0, 6], dist=1) # 添加多個頂點,並定義屬性
G1.add_nodes_from(range(10, 15)) # 向圖 G1 添加頂點 10~14
#==查看頂點和頂點屬性==
print(G1.nodes()) # 查看頂點列表
# [1, 2, 3, 0, 6, 10, 11, 12, 13, 14]
print(G1._node) # 查看頂點屬性
# {1: {'name': 'n1', 'weight': 1.0}, 2: {'date': 'May-16'}, 3: {'dist': 1}, 0: {'dist': 1}, 6: {'dist': 1}, 10: {}, 11: {}, 12: {}, 13: {}, 14: {}}
#==從圖中刪除頂點==
G1.remove_node(1) # 刪除頂點
G1.remove_nodes_from([1, 11, 13, 14]) # 通過頂點標簽的 list 刪除多個頂點
print(G1.nodes()) # 查看頂點
# [2, 3, 0, 6, 10, 12] # 頂點列表
3.2.3 邊的添加、刪除和查看
#====================邊的添加、刪除和查看================
#========邊(edge)的操作========
#==向圖中添加邊==
G1.add_edge(1,5) # 向 G1 添加邊,並自動添加圖中沒有的頂點
G1.add_edge(0,10, weight=2.7) # 向 G1 添加邊,並設置邊的屬性
G1.add_edges_from([(1,2,{'weight':0}), (2,3,{'color':'blue'})]) # 向圖中添加邊,並設置#==屬性==
G1.add_edges_from([(3,6),(1,2),(6,7),(5,10),(0,1)]) # 向圖中添加多條邊
G1.add_weighted_edges_from([(1,2,3.6),[6,12,0.5]]) # 向圖中添加多條賦權邊: (node1,node2,weight)
print(G1.nodes()) # 查看頂點
# [2, 3, 0, 6, 10, 12, 1, 5, 7] # 自動添加瞭圖中沒有的頂點
#==從圖中刪除邊==
G1.remove_edge(0,1) # 從圖中刪除邊 0-1
G1.remove_edges_from([(2,3),(1,5),(6,7)]) # 從圖中刪除多條邊
#==查看邊和邊的屬性==
print(G1.edges) # 查看所有的邊
[(2, 1), (3, 6), (0, 10), (6, 12), (10, 5)]
print(G1.get_edge_data(1,2)) # 查看指定邊的屬性
# {'weight': 3.6}
print(G1[1][2]) # 查看指定邊的屬性
# {'weight': 3.6}
print(G1.edges(data=True)) # 查看所有邊的屬性
# [(2, 1, {'weight': 3.6}), (3, 6, {}), (0, 10, {'weight': 2.7}), (6, 12, {'weight': 0.5}), (10, 5, {})]
3.3 案例
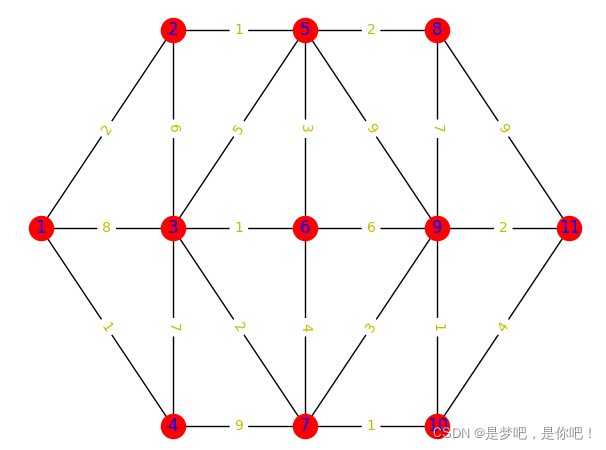
例題 1:已知如圖的有權無向圖,求頂點 v1 到 頂點 v11 的最短路徑。
3.4 Python實現
#========導入相關包=========================
import matplotlib.pyplot as plt # 導入 Matplotlib 工具包
import networkx as nx # 導入 NetworkX 工具包
#======問題:無向圖的最短路問題===============
G1 = nx.Graph() # 創建:空的 無向圖
G1.add_weighted_edges_from([(1,2,2),(1,3,8),(1,4,1),
(2,3,6),(2,5,1),
(3,4,7),(3,5,5),(3,6,1),(3,7,2),
(4,7,9),
(5,6,3),(5,8,2),(5,9,9),
(6,7,4),(6,9,6),
(7,9,3),(7,10,1),
(8,9,7),(8,11,9),
(9,10,1),(9,11,2),
(10,11,4)]) # 向圖中添加多條賦權邊: (node1,node2,weight)
print('nx.info:',G1.nodes) # 返回圖的基本信息,nx.info:返回圖的基本信息
#=======兩個指定頂點之間的最短加權路徑===============
minWPath_v1_v11 = nx.dijkstra_path(G1, source=1, target=11) # 頂點 1 到 頂點 11 的最短加權路徑
print("頂點 v1 到 頂點 v11 的最短加權路徑: ", minWPath_v1_v11)
# 兩個指定頂點之間的最短加權路徑的長度
lMinWPath_v1_v11 = nx.dijkstra_path_length(G1, source=1, target=11) # 最短加權路徑長度
print("頂點 v1 到 頂點 v11 的最短加權路徑長度: ", lMinWPath_v1_v11)
pos = {1: (0,4), 2: (5,7), 3: (5,4), 4: (5,1), 5: (10,7), 6: (10,4), 7: (10,1),
8: (15,7), 9: (15,4), 10: (15,1), 11: (20,4)} # 指定頂點位置,以節點為鍵,位置為值的字典
labels = nx.get_edge_attributes(G1, 'weight') # 設置邊的 labels 為 ‘weight'
nx.draw(G1, pos,node_color = 'r',with_labels=True, font_color='b') # 繪制無向圖,pos 指的是佈局
nx.draw_networkx_edge_labels(G1, pos, edge_labels=labels, font_color='y') # 顯示邊的權值
plt.show()
- 1、Python Network(二)繪圖draw系列draw(),draw_networkx(),draw_networkx_nodes(),draw_networkx_edges()
- 2、用Python的networkx繪制精美網絡圖
3.5 結果
nx.info: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
頂點 v1 到 頂點 v11 的最短加權路徑: [1, 2, 5, 6, 3, 7, 10, 9, 11]
頂點 v1 到 頂點 v11 的最短加權路徑長度: 13
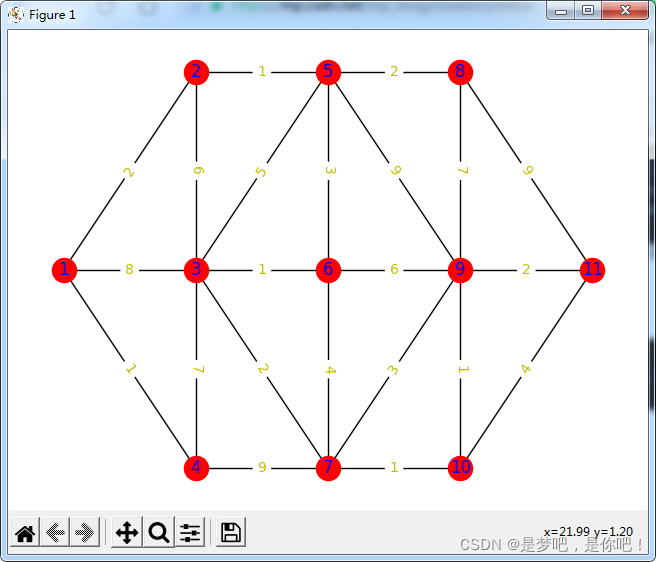
到此這篇關於運籌學-Python實現圖論與最短距離的文章就介紹到這瞭,更多相關Python實現圖論與最短距離內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!
推薦閱讀:
- networkx庫繪制帶權圖給無權圖加權重輸出
- Python實現最短路徑問題的方法
- python光學仿真面向對象光學元件類的實現
- Python實現K-近鄰算法的示例代碼
- Python Opencv使用ann神經網絡識別手寫數字功能