Python實現聚類K-means算法詳解

Posted on by

K-means（K均值）算法是最簡單的一種聚類算法，它期望最小化平方誤差

註：為避免運行時間過長，通常設置一個最大運行輪數或最小調整幅度閾值，若到達最大輪數或調整幅度小於閾值，則停止運行。

下面我們用python來實現一下K-means算法：我們先嘗試手動實現這個算法，再用sklearn庫中的KMeans類來實現。數據我們采用《機器學習》的西瓜數據(P202表9.1):

# 下面的內容保存在 melons.txt 中
# 第一列為西瓜的密度；第二列為西瓜的含糖率。我們要把這30個西瓜分為3類
0.697 0.460
0.774 0.376
0.634 0.264
0.608 0.318
0.556 0.215
0.403 0.237
0.481 0.149
0.437 0.211
0.666 0.091
0.243 0.267
0.245 0.057
0.343 0.099
0.639 0.161
0.657 0.198
0.360 0.370
0.593 0.042
0.719 0.103
0.359 0.188
0.339 0.241
0.282 0.257
0.748 0.232
0.714 0.346
0.483 0.312
0.478 0.437
0.525 0.369
0.751 0.489
0.532 0.472
0.473 0.376
0.725 0.445
0.446 0.459

手動實現

我們用到的庫有matplotlib和numpy，如果沒有需要先用pip安裝一下。

import random
import numpy as np
import matplotlib.pyplot as plt

下面定義一些數據：

k = 3 # 要分的簇數
rnd = 0 # 輪次，用於控制迭代次數（見上文）
ROUND_LIMIT = 100 # 輪次的上限
THRESHOLD = 1e-10 # 單輪改變距離的閾值，若改變幅度小於該閾值，算法終止
melons = [] # 西瓜的列表
clusters = [] # 簇的列表，clusters[i]表示第i簇包含的西瓜

從melons.txt讀取數據，保存在列表中：

f = open('melons.txt', 'r')
for line in f:
	# 把字符串轉化為numpy中的float64類型
    melons.append(np.array(line.split(' '), dtype = np.string_).astype(np.float64))

從 m m m個數據中隨機挑選出 k k k個，對應上面算法的第 1 1 1行：

# random的sample函數從列表中隨機挑選出k個樣本（不重復）。我們在這裡把這些樣本作為均值向量
mean_vectors = random.sample(melons, k)

下面是算法的主要部分。

# 這個while對應上面算法的2-17行
while True:
    rnd += 1 # 輪次增加
    change = 0 # 把改變幅度重置為0

	# 清空對簇的劃分，對應上面算法的第3行
    clusters = []
    for i in range(k):
        clusters.append([])
    # 這個for對應上面算法的4-8行
    for melon in melons:
    	'''
    	argmin 函數找出容器中最小的下標，在這裡這個目標容器是
    	list(map(lambda vec: np.linalg.norm(melon - vec, ord = 2), mean_vectors)),
    	它表示melon與mean_vectors中所有向量的距離列表。
    	(numpy.linalg.norm計算向量的范數,ord = 2即歐幾裡得范數，或模長)
    	'''
        c = np.argmin(
            list(map( lambda vec: np.linalg.norm(melon - vec, ord = 2), mean_vectors))
        )
        clusters[c].append(melon)
	# 這個for對應上面算法的9-16行
    for i in range(k):
    	# 求每個簇的新均值向量
        new_vector = np.zeros((1,2))
        for melon in clusters[i]:
            new_vector += melon
        new_vector /= len(clusters[i])

        # 累加改變幅度並更新均值向量
        change += np.linalg.norm(mean_vectors[i] - new_vector, ord = 2)
        mean_vectors[i] = new_vector
	# 若超過設定的輪次或者變化幅度<預先設定的閾值，結束算法
    if rnd > ROUND_LIMIT or change < THRESHOLD:
        break
print('最終迭代%d輪'%rnd)

最後我們繪圖來觀察一下劃分的結果：

colors = ['red', 'green', 'blue']

# 每個簇換一下顏色，同時迭代簇和顏色兩個列表
for i, col in zip(range(k), colors):
    for melon in clusters[i]:
    	# 繪制散點圖
        plt.scatter(melon[0], melon[1], color = col)
plt.show()

劃分結果（由於最開始的 k k k個均值向量隨機選取，每次劃分的結果可能會不同）:

完整代碼：

import random
import numpy as np
import matplotlib.pyplot as plt

k = 3
rnd = 0
ROUND_LIMIT = 10
THRESHOLD = 1e-10
melons = []
clusters = []
f = open('melons.txt', 'r')
for line in f:
    melons.append(np.array(line.split(' '), dtype = np.string_).astype(np.float64))
mean_vectors = random.sample(melons, k)

while True:
    rnd += 1
    change = 0
    clusters = []
    for i in range(k):
        clusters.append([])
    for melon in melons:
        c = np.argmin(
            list(map( lambda vec: np.linalg.norm(melon - vec, ord = 2), mean_vectors))
        )
        clusters[c].append(melon)
    for i in range(k):
        new_vector = np.zeros((1,2))
        for melon in clusters[i]:
            new_vector += melon
        new_vector /= len(clusters[i])

        change += np.linalg.norm(mean_vectors[i] - new_vector, ord = 2)
        mean_vectors[i] = new_vector

    if rnd > ROUND_LIMIT or change < THRESHOLD:
        break
print('最終迭代%d輪'%rnd)
colors = ['red', 'green', 'blue']
for i, col in zip(range(k), colors):
    for melon in clusters[i]:
        plt.scatter(melon[0], melon[1], color = col)
plt.show()

sklearn庫中的KMeans

這種經典算法顯然不需要我們反復地造輪子，被廣泛使用的python機器學習庫sklearn已經提供瞭該算法的實現。sklearn的官方文檔中給瞭我們一個示例：

>>> from sklearn.cluster import KMeans
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
...               [10, 2], [10, 4], [10, 0]])
>>> kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
>>> kmeans.labels_
array([1, 1, 1, 0, 0, 0], dtype=int32)
>>> kmeans.predict([[0, 0], [12, 3]])
array([1, 0], dtype=int32)
>>> kmeans.cluster_centers_
array([[10.,  2.],
       [ 1.,  2.]])

可以看出，X即要聚類的數據(1,2),(1,4),(1,0)等。
KMeans類的初始化參數n_clusters即簇數 k k k;
random_state是用於初始化選取 k k k個向量的隨機數種子;
kmeans.labels_即每個點所屬的簇；
kmeans.predict方法預測新的數據屬於哪個簇;
kmeans.cluster_centers_返回每個簇的中心。
我們就改造一下這個簡單的示例，完成對上面西瓜的聚類。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

X = []
f = open('melons.txt', 'r')
for line in f:
    X.append(np.array(line.split(' '), dtype = np.string_).astype(np.float64))
kmeans = KMeans(n_clusters = 3, random_state = 0).fit(X)
colors = ['red', 'green', 'blue']
for i, cluster in enumerate(kmeans.labels_):
    plt.scatter(X[i][0], X[i][1], color = colors[cluster])
plt.show()

運行結果如下，可以看到和我們手寫的聚類結果基本一致：

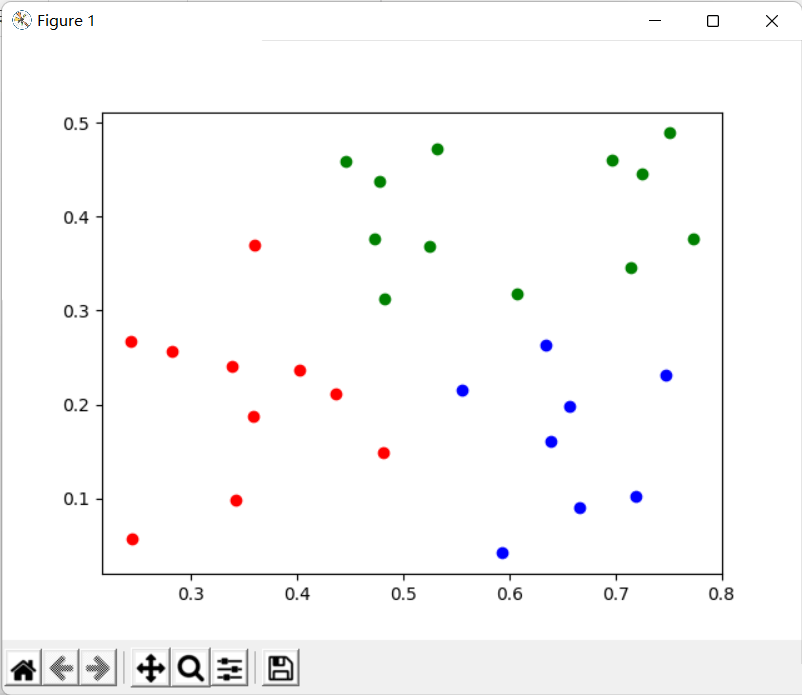
到此這篇關於Python實現聚類K-means算法詳解的文章就介紹到這瞭,更多相關Python K-means算法內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet！

推薦閱讀：