Pytorch中Softmax與LogSigmoid的對比分析

Posted on 2021-06-05 by WalkonNet

Pytorch中Softmax與LogSigmoid的對比

torch.nn.Softmax

作用：

1、將Softmax函數應用於輸入的n維Tensor，重新改變它們的規格，使n維輸出張量的元素位於[0,1]范圍內，並求和為1。

2、返回的Tensor與原Tensor大小相同，值在[0，1]之間。

3、不建議將其與NLLLoss一起使用，可以使用LogSoftmax代替之。

4、Softmax的公式：

在這裡插入圖片描述

參數：

維度，待使用softmax計算的維度。

例子：

# 隨機初始化一個tensor
a = torch.randn(2, 3)
print(a) # 輸出tensor
# 初始化一個Softmax計算對象，在輸入tensor的第2個維度上進行此操作
m = nn.Softmax(dim=1)
# 將a進行softmax操作
output = m(a)
print(output) # 輸出tensor

tensor([[ 0.5283,  0.3922, -0.0484],
        [-1.6257, -0.4775,  0.5645]])
tensor([[0.4108, 0.3585, 0.2307],
        [0.0764, 0.2408, 0.6828]])

可以看見的是，無論輸入的tensor中的值為正或為負，輸出的tensor中的值均為正值，且加和為1。

當m的參數dim=1時，輸出的tensor將原tensor按照行進行softmax操作；當m的參數為dim=0時，輸出的tensor將原tensor按照列進行softmax操作。

深度學習拓展：

一般來說，Softmax函數會用於分類問題上。例如，在VGG等深度神經網絡中，圖像經過一系列卷積、池化操作後，我們可以得到它的特征向量，為瞭進一步判斷此圖像中的物體屬於哪個類別，我們會將該特征向量變為：類別數 * 各類別得分的形式，為瞭將得分轉換為概率值，我們會將該向量再經過一層Softmax處理。

torch.nn.LogSigmoid

公式：

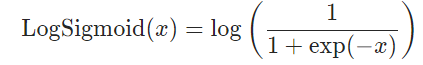
在這裡插入圖片描述

函數圖：

可以見得，函數值在[0, -]之間，輸入值越大函數值距離0越近，在一定程度上解決瞭梯度消失問題。

例子：

a = [[ 0.5283,  0.3922, -0.0484],
    [-1.6257, -0.4775,  0.5645]]
a = torch.tensor(a)
lg = nn.LogSigmoid()
lgoutput = lg(a)
print(lgoutput)

tensor([[-0.4635, -0.5162, -0.7176],
        [-1.8053, -0.9601, -0.4502]])

二者比較：

import torch
import torch.nn as nn
# 設置a為 2*3  的tensor
a = [[ 0.5283,  0.3922, -0.0484],
    [-1.6257, -0.4775,  0.5645]]
a = torch.tensor(a)
print(a)
print('a.mean:', a.mean(1, True)) # 輸出a的 行平均值

m = nn.Softmax(dim=1) # 定義Softmax函數，dim=1表示為按行計算
lg = nn.LogSigmoid() # 定義LogSigmoid函數

output = m(a)
print(output)
# 輸出a經過Softmax的結果的行平均值
print('output.mean:', output.mean(1, True)) 

lg_output = lg(a)
print(lg_output)
# 輸出a經過LogSigmoid的結果的行平均值
print('lgouput.mean:', lg_output.mean(1, True)) 

# 結果：
tensor([[ 0.5283,  0.3922, -0.0484],
        [-1.6257, -0.4775,  0.5645]])
a.mean: tensor(-0.1111)

tensor([[0.4108, 0.3585, 0.2307],
        [0.0764, 0.2408, 0.6828]])
output.mean: tensor([[0.3333], [0.3333]]) # 經過Softmax的結果的行平均值

tensor([[-0.4635, -0.5162, -0.7176],
        [-1.8053, -0.9601, -0.4502]])
lgouput.mean: tensor([[-0.5658], [-1.0719]]) # 經過LogSigmoid的結果的行平均值

由上可知，繼續考慮分類問題，相同的數據，經過Softmax和LogSigmoid處理後，若取最大概率值對應類別作為分類結果，那麼：

1、第一行數據經過Softmax後，會選擇第一個類別；經過LogSigmoid後，會選擇第一個。

2、第二行數據經過Softmax後，會選擇第三個類別；經過LogSigmoid後，會選擇第三個。

3、一般來說，二者在一定程度上區別不是很大，由於sigmoid函數存在梯度消失問題，所以被使用的場景不多。

4、但是在多分類問題上，可以嘗試選擇Sigmoid函數來作為分類函數，因為Softmax在處理多分類問題上，會更容易出現各項得分十分相近的情況。瓶頸值可以根據實際情況定。

nn.Softmax()與nn.LogSoftmax()

nn.Softmax()計算出來的值，其和為1，也就是輸出的是概率分佈，具體公式如下：

這保證輸出值都大於0，在0,1范圍內。

而nn.LogSoftmax()公式如下：

由於softmax輸出都是0-1之間的，因此logsofmax輸出的是小於0的數，

softmax求導：

logsofmax求導：

例子：

import torch.nn as nn
import torch
import numpy as np

layer1=nn.Softmax()
layer2=nn.LogSoftmax()
 
input=np.asarray([2,3])
input=Variable(torch.Tensor(input))
 
output1=layer1(input)
output2=layer2(input)
print('output1:',output1)
print('output2:',output2)

輸出：

output1: Variable containing:
0.2689
0.7311
[torch.FloatTensor of size 2]

output2: Variable containing:
-1.3133
-0.3133
[torch.FloatTensor of size 2]

以上為個人經驗，希望能給大傢一個參考，也希望大傢多多支持WalkonNet。

Pytorch中Softmax與LogSigmoid的對比分析