詳解Dijkstra算法之最短路徑問題
一、最短路徑問題介紹
問題解釋:
從圖中的某個頂點出發到達另外一個頂點的所經過的邊的權重和最小的一條路徑,稱為最短路徑
解決問題的算法:
- 迪傑斯特拉算法(Dijkstra算法)
- 弗洛伊德算法(Floyd算法)
- SPFA算法
這篇博客,我們就對Dijkstra算法來做一個詳細的介紹
二、Dijkstra算法介紹
2.1、算法特點
迪科斯徹算法使用瞭廣度優先搜索解決賦權有向圖或者無向圖的單源最短路徑問題,算法最終得到一個最短路徑樹。該算法常用於路由算法或者作為其他圖算法的一個子模塊。
2.2、算法的思路
Dijkstra算法采用的是一種貪心的策略,聲明一個數組dis來保存源點到各個頂點的最短距離和一個保存已經找到瞭最短路徑的頂點的集合:T,初始時,原點 s 的路徑權重被賦為 0 (dis[s] = 0)。若對於頂點 s 存在能直接到達的邊(s,m),則把dis[m]設為w(s, m),同時把所有其他(s不能直接到達的)頂點的路徑長度設為無窮大。初始時,集合T隻有頂點s。
然後,從dis數組選擇最小值,則該值就是源點s到該值對應的頂點的最短路徑,並且把該點加入到T中,OK,此時完成一個頂點,然後,我們需要看看新加入的頂點是否可以到達其他頂點並且看看通過該頂點到達其他點的路徑長度是否比源點直接到達短,如果是,那麼就替換這些頂點在dis中的值。 然後,又從dis中找出最小值,重復上述動作,直到T中包含瞭圖的所有頂點。
三、Dijkstra算法示例演示
下面我求下圖,從頂點v1到其他各個頂點的最短路徑

首先第一步,我們先聲明一個dis數組,該數組初始化的值為:

我們的頂點集T的初始化為:T={v1}
既然是求 v1頂點到其餘各個頂點的最短路程,那就先找一個離 1 號頂點最近的頂點。通過數組 dis 可知當前離v1頂點最近是 v3頂點。當選擇瞭 2 號頂點後,dis[2](下標從0開始)的值就已經從“估計值”變為瞭“確定值”,即 v1頂點到 v3頂點的最短路程就是當前 dis[2]值。將V3加入到T中。
為什麼呢?因為目前離 v1頂點最近的是 v3頂點,並且這個圖所有的邊都是正數,那麼肯定不可能通過第三個頂點中轉,使得 v1頂點到 v3頂點的路程進一步縮短瞭。因為 v1頂點到其它頂點的路程肯定沒有 v1到 v3頂點短.
OK,既然確定瞭一個頂點的最短路徑,下面我們就要根據這個新入的頂點V3會有出度,發現以v3 為弧尾的有: < v3,v4 >,那麼我們看看路徑:v1–v3–v4的長度是否比v1–v4短,其實這個已經是很明顯的瞭,因為dis[3]代表的就是v1–v4的長度為無窮大,而v1–v3–v4的長度為:10+50=60,所以更新dis[3]的值,得到如下結果:

因此 dis[3]要更新為 60。這個過程有個專業術語叫做“松弛”。即 v1頂點到 v4頂點的路程即 dis[3],通過 < v3,v4> 這條邊松弛成功。這便是 Dijkstra 算法的主要思想:通過“邊”來松弛v1頂點到其餘各個頂點的路程。
然後,我們又從除dis[2]和dis[0]外的其他值中尋找最小值,發現dis[4]的值最小,通過之前是解釋的原理,可以知道v1到v5的最短距離就是dis[4]的值,然後,我們把v5加入到集合T中,然後,考慮v5的出度是否會影響我們的數組dis的值,v5有兩條出度:< v5,v4>和 < v5,v6>,然後我們發現:v1–v5–v4的長度為:50,而dis[3]的值為60,所以我們要更新dis[3]的值.另外,v1-v5-v6的長度為:90,而dis[5]為100,所以我們需要更新dis[5]的值。更新後的dis數組如下圖:

然後,繼續從dis中選擇未確定的頂點的值中選擇一個最小的值,發現dis[3]的值是最小的,所以把v4加入到集合T中,此時集合T={v1,v3,v5,v4},然後,考慮v4的出度是否會影響我們的數組dis的值,v4有一條出度:< v4,v6>,然後我們發現:v1–v5–v4–v6的長度為:60,而dis[5]的值為90,所以我們要更新dis[5]的值,更新後的dis數組如下圖:

然後,我們使用同樣原理,分別確定瞭v6和v2的最短路徑,最後dis的數組的值如下:

因此,從圖中,我們可以發現v1-v2的值為:∞,代表沒有路徑從v1到達v2。所以我們得到的最後的結果為:
起點 終點 最短路徑 長度
v1 v2 無 ∞
v3 {v1,v3} 10
v4 {v1,v5,v4} 50
v5 {v1,v5} 30
v6 {v1,v5,v4,v6} 60
四、Dijkstra算法的代碼實現(c++)
Dijkstra.h文件的代碼
//@盡量寫出完美的程序
#pragma once
//#pragma once是一個比較常用的C/C++雜註,
//隻要在頭文件的最開始加入這條雜註,
//就能夠保證頭文件隻被編譯一次。
#include<iostream>
#include<string>
using namespace std;
/*
本程序是使用Dijkstra算法實現求解最短路徑的問題
采用的鄰接矩陣來存儲圖
*/
//記錄起點到每個頂點的最短路徑的信息
struct Dis {
string path;
int value;
bool visit;
Dis() {
visit = false;
value = 0;
path = "";
}
};
class Graph_DG {
private:
int vexnum; //圖的頂點個數
int edge; //圖的邊數
int **arc; //鄰接矩陣
Dis * dis; //記錄各個頂點最短路徑的信息
public:
//構造函數
Graph_DG(int vexnum, int edge);
//析構函數
~Graph_DG();
// 判斷我們每次輸入的的邊的信息是否合法
//頂點從1開始編號
bool check_edge_value(int start, int end, int weight);
//創建圖
void createGraph();
//打印鄰接矩陣
void print();
//求最短路徑
void Dijkstra(int begin);
//打印最短路徑
void print_path(int);
};
Dijkstra.cpp文件的代碼
#include"Dijkstra.h"
//構造函數
Graph_DG::Graph_DG(int vexnum, int edge) {
//初始化頂點數和邊數
this->vexnum = vexnum;
this->edge = edge;
//為鄰接矩陣開辟空間和賦初值
arc = new int*[this->vexnum];
dis = new Dis[this->vexnum];
for (int i = 0; i < this->vexnum; i++) {
arc[i] = new int[this->vexnum];
for (int k = 0; k < this->vexnum; k++) {
//鄰接矩陣初始化為無窮大
arc[i][k] = INT_MAX;
}
}
}
//析構函數
Graph_DG::~Graph_DG() {
delete[] dis;
for (int i = 0; i < this->vexnum; i++) {
delete this->arc[i];
}
delete arc;
}
// 判斷我們每次輸入的的邊的信息是否合法
//頂點從1開始編號
bool Graph_DG::check_edge_value(int start, int end, int weight) {
if (start<1 || end<1 || start>vexnum || end>vexnum || weight < 0) {
return false;
}
return true;
}
void Graph_DG::createGraph() {
cout << "請輸入每條邊的起點和終點(頂點編號從1開始)以及其權重" << endl;
int start;
int end;
int weight;
int count = 0;
while (count != this->edge) {
cin >> start >> end >> weight;
//首先判斷邊的信息是否合法
while (!this->check_edge_value(start, end, weight)) {
cout << "輸入的邊的信息不合法,請重新輸入" << endl;
cin >> start >> end >> weight;
}
//對鄰接矩陣對應上的點賦值
arc[start - 1][end - 1] = weight;
//無向圖添加上這行代碼
//arc[end - 1][start - 1] = weight;
++count;
}
}
void Graph_DG::print() {
cout << "圖的鄰接矩陣為:" << endl;
int count_row = 0; //打印行的標簽
int count_col = 0; //打印列的標簽
//開始打印
while (count_row != this->vexnum) {
count_col = 0;
while (count_col != this->vexnum) {
if (arc[count_row][count_col] == INT_MAX)
cout << "∞" << " ";
else
cout << arc[count_row][count_col] << " ";
++count_col;
}
cout << endl;
++count_row;
}
}
void Graph_DG::Dijkstra(int begin){
//首先初始化我們的dis數組
int i;
for (i = 0; i < this->vexnum; i++) {
//設置當前的路徑
dis[i].path = "v" + to_string(begin) + "-->v" + to_string(i + 1);
dis[i].value = arc[begin - 1][i];
}
//設置起點的到起點的路徑為0
dis[begin - 1].value = 0;
dis[begin - 1].visit = true;
int count = 1;
//計算剩餘的頂點的最短路徑(剩餘this->vexnum-1個頂點)
while (count != this->vexnum) {
//temp用於保存當前dis數組中最小的那個下標
//min記錄的當前的最小值
int temp=0;
int min = INT_MAX;
for (i = 0; i < this->vexnum; i++) {
if (!dis[i].visit && dis[i].value<min) {
min = dis[i].value;
temp = i;
}
}
//cout << temp + 1 << " "<<min << endl;
//把temp對應的頂點加入到已經找到的最短路徑的集合中
dis[temp].visit = true;
++count;
for (i = 0; i < this->vexnum; i++) {
//註意這裡的條件arc[temp][i]!=INT_MAX必須加,不然會出現溢出,從而造成程序異常
if (!dis[i].visit && arc[temp][i]!=INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) {
//如果新得到的邊可以影響其他為訪問的頂點,那就就更新它的最短路徑和長度
dis[i].value = dis[temp].value + arc[temp][i];
dis[i].path = dis[temp].path + "-->v" + to_string(i + 1);
}
}
}
}
void Graph_DG::print_path(int begin) {
string str;
str = "v" + to_string(begin);
cout << "以"<<str<<"為起點的圖的最短路徑為:" << endl;
for (int i = 0; i != this->vexnum; i++) {
if(dis[i].value!=INT_MAX)
cout << dis[i].path << "=" << dis[i].value << endl;
else {
cout << dis[i].path << "是無最短路徑的" << endl;
}
}
}
main.cpp文件的代碼
#include"Dijkstra.h"
//檢驗輸入邊數和頂點數的值是否有效,可以自己推算為啥:
//頂點數和邊數的關系是:((Vexnum*(Vexnum - 1)) / 2) < edge
bool check(int Vexnum, int edge) {
if (Vexnum <= 0 || edge <= 0 || ((Vexnum*(Vexnum - 1)) / 2) < edge)
return false;
return true;
}
int main() {
int vexnum; int edge;
cout << "輸入圖的頂點個數和邊的條數:" << endl;
cin >> vexnum >> edge;
while (!check(vexnum, edge)) {
cout << "輸入的數值不合法,請重新輸入" << endl;
cin >> vexnum >> edge;
}
Graph_DG graph(vexnum, edge);
graph.createGraph();
graph.print();
graph.Dijkstra(1);
graph.print_path(1);
system("pause");
return 0;
}
輸入:
6 8
1 3 10
1 5 30
1 6 100
2 3 5
3 4 50
4 6 10
5 6 60
5 4 20
輸出:
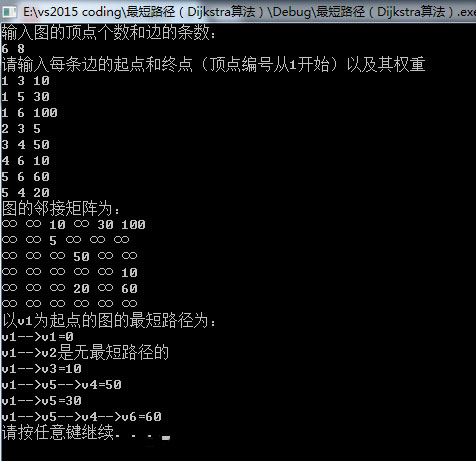
從輸出可以看出,程序的結果和我們之前手動計算的結果是一樣的。
以上就是詳解Dijkstra算法之最短路徑問題的詳細內容,更多關於c++實現Dijkstra算法 最短路徑 的資料請關註WalkonNet其它相關文章!