詳解Java如何實現小頂堆和大頂堆
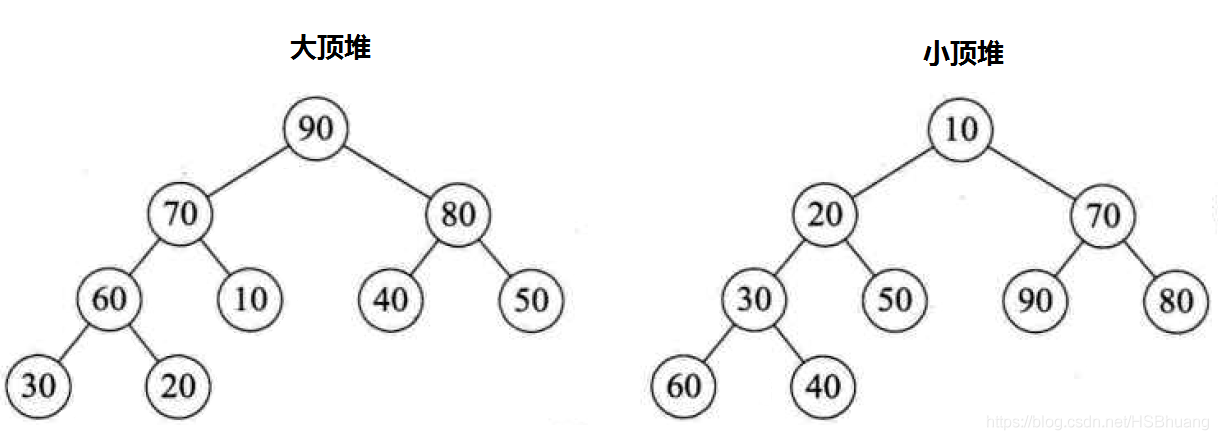
大頂堆
每個結點的值都大於或等於其左右孩子結點的值
小頂堆
每個結點的值都小於或等於其左右孩子結點的值
對比圖
實現代碼
public class HeapNode{
private int size;//堆大小
private int[] heap;//保存堆數組
//初始化堆
public HeapNode(int n) {
heap = new int[n];
size = 0;
}
//小頂堆建堆
public void minInsert(int key){
int i = this.size;
if (i==0) heap[0] = key;
else {
while (i>0 && heap[i/2]>key){
heap[i] = heap[i/2];
i = i/2;
}
heap[i] = key;
}
this.size++;
}
//大頂堆建堆
public void maxInsert(int key){
int i = this.size;
if (i==0) heap[0] = key;
else {
while (i>0 && heap[i/2]<key){
heap[i] = heap[i/2];
i = i/2;
}
heap[i] = key;
}
this.size++;
}
//小頂堆刪除
public int minDelete(){
if (this.size==0) return -1;
int top = heap[0];
int last = heap[this.size-1];
heap[0] = last;
this.size--;
//堆化
minHeapify(0);
return top;
}
//大頂堆刪除
public int maxDelete(){
if (this.size==0) return -1;
int top = heap[0];
int last = heap[this.size-1];
heap[0] = last;
this.size--;
//堆化
maxHeapify(0);
return top;
}
//小頂堆化
public void minHeapify(int i){
int L = 2*i,R=2*i+1,min;
if (L<=size && heap[L] < heap[i]) min = L;
else min = i;
if (R <= size && heap[R] < heap[min]) min = R;
if (min!=i){
int t = heap[min];
heap[min] = heap[i];
heap[i] = t;
minHeapify(min);
}
}
//大頂堆化
public void maxHeapify(int i){
int L = 2*i,R=2*i+1,max;
if (L<=size && heap[L] > heap[i]) max = L;
else max = i;
if (R <= size && heap[R] > heap[max]) max = R;
if (max!=i){
int t = heap[max];
heap[max] = heap[i];
heap[i] = t;
maxHeapify(max);
}
}
//輸出堆
public void print(){
for (int i = 0; i < this.size; i++) {
System.out.print(heap[i]+" ");
}
System.out.println();
}
}
測試
public class Heap {
static int[] a = {5,3,6,4,2,1};
static int n = a.length;
public static void main(String[] args){
HeapNode heapNode = new HeapNode(n);
for (int i = 0; i < n; i++) {
heapNode.maxInsert(a[i]);
}
heapNode.print();
for (int i = 0; i < n; i++) {
int min = heapNode.maxDelete();
System.out.print("堆頂:"+min+" 剩下堆元素:");
heapNode.print();
}
}
}
結果

到此這篇關於詳解Java如何實現小頂堆和大頂堆的文章就介紹到這瞭,更多相關Java實現小頂堆和大頂堆內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!