python 基於空間相似度的K-means軌跡聚類的實現
這裡分享一些軌跡聚類的基本方法,涉及軌跡距離的定義、kmeans聚類應用。
需要使用的python庫如下
import pandas as pd import numpy as np import random import os import matplotlib.pyplot as plt import seaborn as sns from scipy.spatial.distance import cdist from itertools import combinations from joblib import Parallel, delayed from tqdm import tqdm
數據讀取
假設數據是每一條軌跡一個excel文件,包括經緯度、速度、方向的航班數據。我們從文件中讀取該數據,保存在字典中。
獲取數據的地址,假設在多個文件中
def get_alldata_path(path):
all_path = pd.DataFrame(columns=['path_root','path0','path1','path2','path','datalist'])
path0 = os.listdir(path)
for path_temp0 in path0:
path1 = os.listdir(path+path_temp0)
for path_temp1 in path1:
path2 = os.listdir(path+path_temp0+'\\'+path_temp1)
for path_temp2 in path2:
path3 = os.listdir(path+path_temp0+'\\'+path_temp1+'\\'+path_temp2)
all_path.loc[all_path.shape[0]] = [path,path_temp0,path_temp1,path_temp2,
path+path_temp0+'\\'+path_temp1+'\\'+path_temp2+'\\',
path3]
return all_path
這樣你就可以得到你的數據的地址,方便後面讀取需要的數據
#設置數據根目錄 path = 'yourpath' #獲取所有數據地址 data_path = get_alldata_path(path)
讀取數據,保存成字典格式,字典的key是這條軌跡的名稱,value值是一個DataFrame,需要包含經緯度信息。
def read_data(data_path,idxs):
'''
功能:讀取數據
'''
data = {}
for idx in idxs:
path_idx = data_path['path'][idx]
for dataname in data_path['datalist'][idx]:
temp = pd.read_excel(path_idx+dataname,header=None)
temp = temp.loc[:,[4,5,6,8]]
temp.replace('none',np.nan,inplace=True)
temp.replace('Trak',np.nan,inplace=True)
temp = temp.dropna().astype(float)
temp.columns = ['GPSLongitude','GPSLatitude','direction','speed']
data[str(idx)+'_'+dataname] = temp
return data
讀取你想要的數據,前面讀取到的地址也是一個DataFrame,選擇你想要進行聚類的數據讀取進來。
#讀取你想要的數據 idxs = [0,1,2] data = read_data(data_path,idxs)
定義不同軌跡間的距離
這裡使用瞭雙向的Hausdorff距離(雙向豪斯多夫距離)
給定兩條軌跡A和B,其中軌跡A上有n個點,軌跡B上有m個點。它們之間的空間相似距離d定義為:
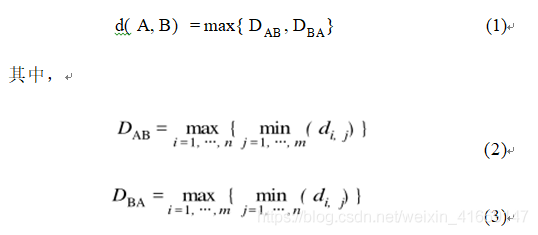
其中,di ,j 是一條軌跡上的第 i個點到另一條軌跡上的 第 j 個 點之間的多因素歐氏距離。可見, 如果軌跡 A 和 B 越相似, 它們之間的距離就越小, 反之則越大。
def OneWayHausdorffDistance(ptSetA, ptSetB):
# 計算任意向量之間的距離,假設ptSetA有n個向量,ptSetB有m個向量
# 得到矩陣C(n行m列)Cij代表A中都第i個向量到B中第j向量都距離
dist = cdist(ptSetA, ptSetB, metric='euclidean')
# np.min(dist,axis=1):計算每一行的的最小值
# 即:固定點集A的值,求點集A中到集合B的最小值
return np.max(np.min(dist, axis=1))
# 計算雙向的Hausdorff距離=====>H(ptSetA,ptSetB)=max(h(ptSetA,ptSetB),h(ptSetB,ptSetA))
# ptSetA:輸入的第一個點集
# ptSetB:輸入的第二個點集
# Hausdorff距離度量瞭兩個點集間的最大不匹配程度
def HausdorffDistance(ptSetA, ptSetB):
# 計算雙向的Hausdorff距離距離
res = np.array([
OneWayHausdorffDistance(ptSetA, ptSetB),
OneWayHausdorffDistance(ptSetB, ptSetA)
])
return np.max(res)
計算距離矩陣
每個軌跡數據都包含經緯度、速度、方向,分別計算距離,然後根據一定的比例相加,活動最終的距離。
def DistanceMat(data,w=[0.7,0.2,0.1]):
'''
功能:計算軌跡段的距離矩陣
輸出:距離矩陣
'''
#要計算的組合
ptCom = list(combinations(list(data.keys()),2))
#基於軌跡的距離
distance_tra = Parallel(n_jobs=8,verbose=False)(delayed(HausdorffDistance)(
data[ptSet1][['GPSLongitude','GPSLatitude']],data[ptSet2][['GPSLongitude','GPSLatitude']]
) for ptSet1,ptSet2 in ptCom)
distancemat_tra = pd.DataFrame(ptCom)
distancemat_tra['distance'] = distance_tra
distancemat_tra = distancemat_tra.pivot(index=0,columns=1,values='distance')
for pt1 in data.keys():
distancemat_tra.loc[str(pt1),str(pt1)] = 0
distancemat_tra = distancemat_tra.fillna(0)
distancemat_tra = distancemat_tra.loc[list(data.keys()),list(data.keys())]
distancemat_tra = distancemat_tra+distancemat_tra.T
#基於方向的距離
distance_speed = Parallel(n_jobs=8,verbose=False)(delayed(HausdorffDistance)(
data[ptSet1][['speed']],data[ptSet2][['speed']]
) for ptSet1,ptSet2 in ptCom)
distancemat_speed = pd.DataFrame(ptCom)
distancemat_speed['distance'] = distance_speed
distancemat_speed = distancemat_speed.pivot(index=0,columns=1,values='distance')
for pt1 in data.keys():
distancemat_speed.loc[str(pt1),str(pt1)] = 0
distancemat_speed = distancemat_speed.fillna(0)
distancemat_speed = distancemat_speed.loc[list(data.keys()),list(data.keys())]
distancemat_speed = distancemat_speed+distancemat_speed.T
#基於方向的距離
distance_direction = Parallel(n_jobs=8,verbose=False)(delayed(HausdorffDistance)(
data[ptSet1][['direction']],data[ptSet2][['direction']]
) for ptSet1,ptSet2 in ptCom)
distancemat_direction = pd.DataFrame(ptCom)
distancemat_direction['distance'] = distance_direction
distancemat_direction = distancemat_direction.pivot(index=0,columns=1,values='distance')
for pt1 in data.keys():
distancemat_direction.loc[str(pt1),str(pt1)] = 0
distancemat_direction = distancemat_direction.fillna(0)
distancemat_direction = distancemat_direction.loc[list(data.keys()),list(data.keys())]
distancemat_direction = distancemat_direction+distancemat_direction.T
distancemat_tra = (distancemat_tra-distancemat_tra.min().min())/(distancemat_tra.max().max()-distancemat_tra.min().min())
distancemat_speed = (distancemat_speed-distancemat_speed.min().min())/(distancemat_speed.max().max()-distancemat_speed.min().min())
distancemat_direction = (distancemat_direction-distancemat_direction.min().min())/(distancemat_direction.max().max()-distancemat_direction.min().min())
distancemat = w[0]*distancemat_tra+w[1]*distancemat_speed+w[2]*distancemat_direction
return distancemat
使用前面讀取的數據,計算不同軌跡間的距離矩陣,缺點在於計算時間會隨著軌跡數的增大而指數增長。
distancemat = DistanceMat(data,w=[0.7,0.2,0.1])
k-means聚類
獲得瞭不同軌跡間的距離矩陣後,就可以進行聚類瞭。這裡選擇k-means,為瞭得到更好的結果,聚類前的聚類中心選取也經過瞭一些設計,排除瞭隨機選擇,而是選擇盡可能遠的軌跡點作為 初始中心。
初始化聚類“中心”。隨機選取一條軌跡作為第一類的中心, 即選取一個軌跡序列作為聚類的初始“中心。然後在剩下的 L – 1 個序列中選取一個序列 X 2 作為第二類的中心 C 2 , 設定一個閾值 q, 使其到第一類的中心 C 1 的距離大於q。
class KMeans:
def __init__(self,n_clusters=5,Q=74018,max_iter=150):
self.n_clusters = n_clusters #聚類數
self.Q = Q
self.max_iter = max_iter # 最大迭代數
def fit(self,distancemat):
#選擇初始中心
best_c = random.sample(distancemat.columns.tolist(),1)
for i in range(self.n_clusters-1):
best_c += random.sample(distancemat.loc[(distancemat[best_c[-1]]>self.Q)&(~distancemat.index.isin(best_c))].index.tolist(),1)
center_init = distancemat[best_c] #選擇最小的樣本組合為初始質心
self._init_center = center_init
#迭代停止條件
iter_ = 0
run = True
#開始迭代
while (iter_<self.max_iter)&(run==True):
#聚類聚類標簽更新
labels_ = np.argmin(center_init.values,axis=1)
#聚類中心更新
best_c_ = [distancemat.iloc[labels_== i,labels_==i].sum().idxmin() for i in range(self.n_clusters)]
center_init_ = distancemat[best_c_]
#停止條件
iter_ += 1
if best_c_ == best_c:
run = False
center_init = center_init_.copy()
best_c = best_c_.copy()
#記錄數據
self.labels_ = np.argmin(center_init.values,axis=1)
self.center_tra = center_init.columns.values
self.num_iter = iter_
self.sse = sum([sum(center_init.iloc[self.labels_==i,i]) for i in range(self.n_clusters)])
應用聚類,根據平方誤差和SSE結合手肘法確定最佳的聚類數,使用最佳的聚類數獲得最後聚類模型。
#聚類,保存不同的sse
SSE = []
for i in range(2,30):
kmeans = KMeans(n_clusters=i,Q=0.01,max_iter=150)
kmeans.fit(distancemat)
SSE.append(kmeans.sse)
#畫圖
plt.figure(0)
plt.plot(SSE)
plt.show()
#使用最好的結果進行聚類
n_clusters=12
kmeans = KMeans(n_clusters=n_clusters,Q=0.01,max_iter=150)
kmeans.fit(distancemat)
kmeans.sse #輸出sse
kmeans.labels_ #輸出標簽
kmeans.center_tra #輸出聚類中心
#畫圖,不同類的軌跡使用不同的顏色
plt.figure(1)
for i in range(n_clusters):
for name in distancemat.columns[kmeans.labels_==i]:
plt.plot(data[name].loc[:,'GPSLongitude'],data[name].loc[:,'GPSLatitude'],c=sns.xkcd_rgb[list(sns.xkcd_rgb.keys())[i]])
plt.show()
#保存每一個軌跡屬於哪一類
kmeans_result = pd.DataFrame(columns=['label','id'])
for i in range(n_clusters):
kmeans_result.loc[i] = [i,distancemat.columns[kmeans.labels_==i].tolist()]
到此這篇關於python 基於空間相似度的K-means軌跡聚類的實現的文章就介紹到這瞭,更多相關python K-means軌跡聚類內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!
推薦閱讀:
- python中k-means和k-means++原理及實現
- 人工智能——K-Means聚類算法及Python實現
- Python sklearn中的K-Means聚類使用方法淺析
- Python+OpenCV實戰之利用 K-Means 聚類進行色彩量化
- pandas返回缺失值位置的方法實例教程