C語言植物大戰數據結構二叉樹堆
“竹杖芒鞋輕勝馬,誰怕?一蓑煙雨任平生”
C語言朱武大戰數據結構專欄
C語言植物大戰數據結構快速排序圖文示例
C語言植物大戰數據結構希爾排序算法
C語言植物大戰數據結構堆排序圖文示例
C語言植物大戰數據結構二叉樹遞歸
前言
此篇詳細實現二叉樹中的一個順序結構的實現——堆。並實現堆排序重點是堆的規律和堆的實現
堆的概念
堆:將一些元素按完全二叉樹的順序存儲方式存儲在一個一維數組中。這就是堆。完全二叉樹:通俗講就是隻有最後一層的節點可以滿,也可以不滿。但是最後一層之前的節點要滿,這就叫做完全二叉樹。
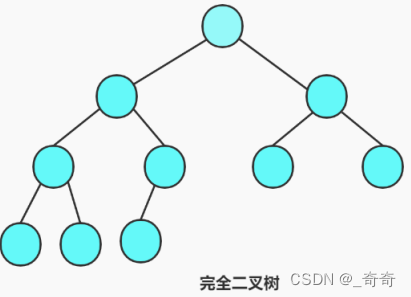
小堆大堆:將根節點最大的堆叫做最大堆或大根堆,根節點最小的堆叫做最小堆或小根堆。(必須滿足堆的性質)
堆的性質:
1.堆中某個節點的值總是不大於或不小於其父節點的值
2.堆總是一棵完全二叉樹。
註意:
1.普通的二叉樹是不適合用數組來存儲的,因為可能會存在大量的空間浪費。而完全二叉樹更適合使用順序結構存儲。
2.現實中我們通常把堆(一種特殊的二叉樹)使用順序結構的數組來存儲。
3.需要註意的是這裡的堆和操作系統虛擬進程地址空間中的堆是兩回事,一個是數據結構,一個是操作系統中管理內存的一塊區域分段。
接下來我們用純C實現小堆
創建結構體
因為完全二叉樹更適合使用順序結構存儲。而堆就是完全二叉樹,所以我們需要創建順序表
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;//a指向隻一個堆數組
size_t size;//記錄堆的大小
size_t capacity;//堆的最大容量
}HP;
初始化結構體
這一步必須要有,相當於創建變量瞭。
//初始化結構體
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
銷毀結構體
因為是動態版的順序表,有動態開辟就需要動態內存釋放,也就是free掉a所指向的空間。
//銷毀結構體
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
//free掉及時置空,防止野指針
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
向堆中插入數據
在插入數據之前,我們需要先知道堆的一個技巧。
1.堆的物理結構和邏輯結構
前面的步驟打造瞭一個堆的輪廓,你說它是堆吧,其實本質就是一個物理結構在內存中連續的順序表罷瞭。也就是數組。如圖下標從0開始。

但是要用到它的邏輯結構,需要把它想象成一個完全二叉樹,就是下面圖片這個樣子。
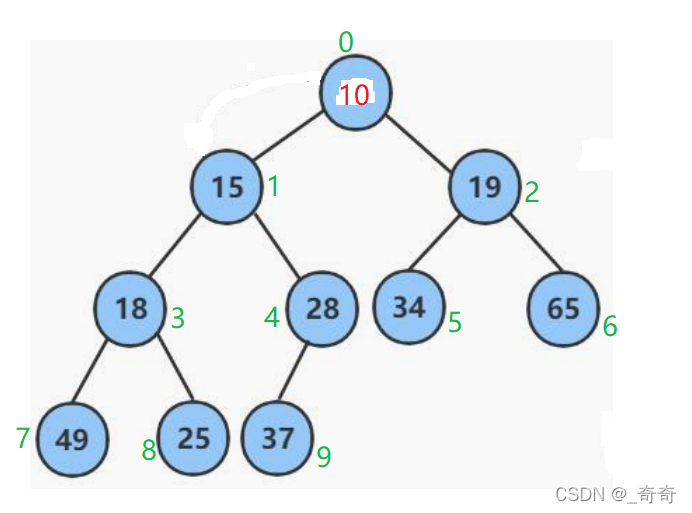
好瞭,現在我們要向堆中插入數據瞭,因為順序表尾插效率高O(1),且尾插不會大幅度改變堆的結構。所以插入數據指的是尾插。
2.完全二叉樹下標規律
註意:
1.尾插註意的是size的大小,size一直指向的是即將插入的那個空間。
2.和順序表唯一不同的是尾插後需要向上調整數據,保持小堆的從上往下依次增大的結構
3.堆中的下標是有規律的。規律公式如下
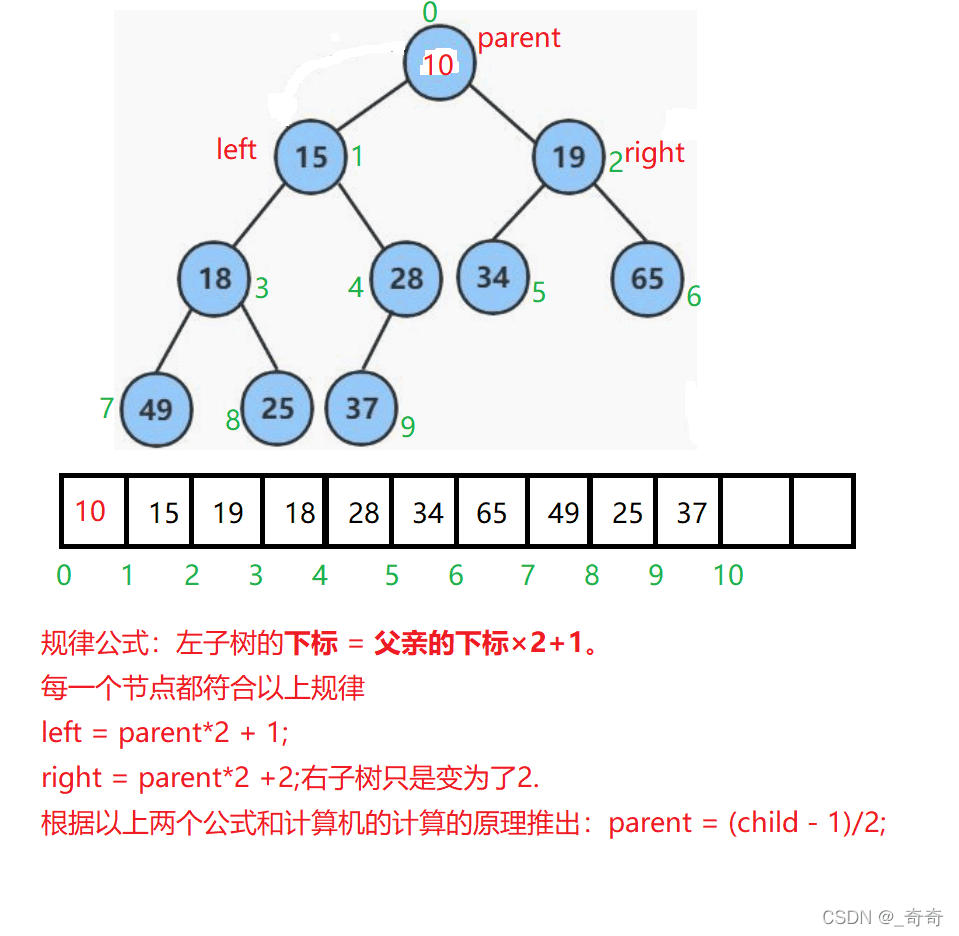
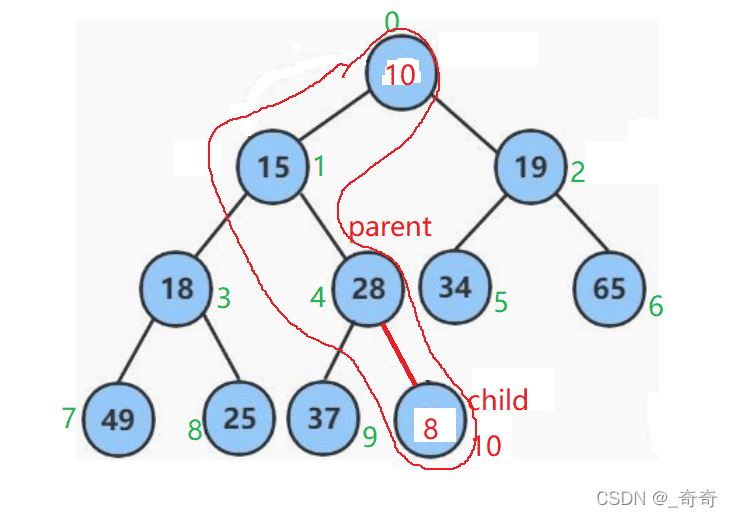
這裡需要強調的是對於父親下標的計算。父親的下標計算公式為:parent = (child – 1) / 2;舉個例子。因為假如左子樹是7,右子樹是8。7-1初以2是3, 但8-1初以2是3.5。但是計算機計算的結果也是3。
結論:所以管他是左子樹,還是右子樹,都能計算出其父親的下標。
3.插入數據思路
最重要的思路是向上調整思想
我們以向堆中插入一個8為例。
因為size指向的是順序表中即將插入的位置,所以直接插入就好瞭,但要及時讓size++。
註意:尾插後size還需要指向下一個即將插入的位置。如圖
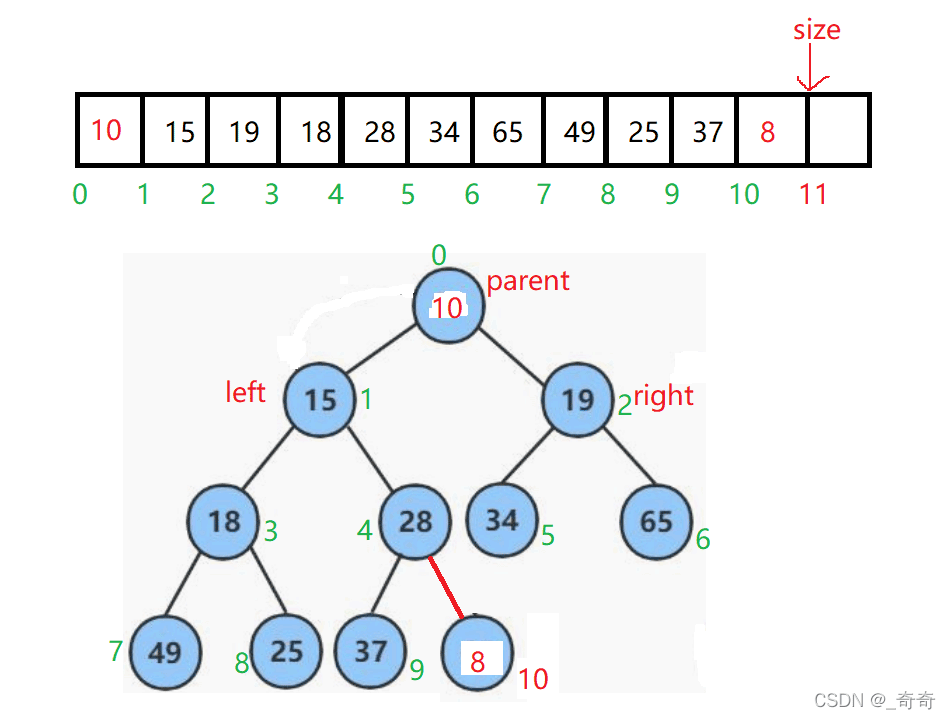
然後開始向上調整8的位置。
思路:
1.讓child依次和其parent比較,假如child小的話就交換兩者的數據,使child的值依次向上走。然後迭代執行child = parent;parent = (child – 1) / 2;用來迭代parent和child的位置,直到child等於0。結束循環。
2.我覺得思路不難,難在把思路轉換為代碼然後實現。
3.註意實參傳遞的實參分別是數組首元素的地址,和新插入元素的下標。
//交換
void HeapSwap(HPDataType* pa, HPDataType* pb)
{
HPDataType tmp = *pa;
*pa = *pb;
*pb = tmp;
}
//向上調整
void AdjustUp(HPDataType* a, size_t child)
{
size_t parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
//因為需要多次用到交換算法,所以寫成一個函數,方便調用。
HeapSwap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//插入堆
void HeapPush(HP* php, HPDataType x)
{
assert(php);
//除瞭AdjustUp
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
//註意realloc的用法
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType)* newcapacity);
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size] = x;
++php->size;
//唯一不同於順序表的地方,向上調整算法
AdjustUp(php->a, php->size - 1);
}
依次打印堆的值
插入堆後,為瞭可視化,我們還是打印一下看看效果。
void HeapPrint(HP* php)
{
assert(php);
for (size_t i = 0; i < php->size; ++i)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
刪除堆頂的值
刪除也是一門藝術。今天的我是站在巨人的肩膀上學習堆的刪除。
大佬們的算法思路是:
1.先讓堆頂的值和堆尾的值交換O(1),然後刪除O(1)交換後堆尾的值。
2.再使用向下調整O(logN)算法,先比較left和right哪個小,誰小就讓parent和誰交換,然後依次迭代,使堆頂的值向下調整。直到child大於size結束循環。
因為這樣的時間復雜度是相當牛的。
註意:這裡有幾個地方代碼技巧非常絕。
1.假設左子樹就是最小的值。然後比較左右子樹的大小後進行調整到底誰是最小的就OK瞭。這是非常的絕。因為你需要關註到底是左子樹小還是右子樹小!
//非常絕的一個思路
if (child+1 < size &&
a[child + 1] < a[child])
{
++child;
}
刪除代碼如下。
//向下調整
AdjustDown(HPDataType* a,size_t size, size_t root)
{
size_t parent= root;
size_t child= parent * 2 + 1;
while (child < size)
{
//判斷哪個孩子小。
if (child+1 < size && a[child + 1] < a[child])
{
++child;
}
//交換父親和孩子的值
if (a[child] < a[parent])
{
HeapSwap(&a[parent], &a[child]);
//迭代
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//刪除堆頂的值
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
//交換堆頂和堆尾的值。然後刪除堆尾的值
HeapSwap(php->a, &php->a[php->size - 1]);
--php->size;
//向下調整
AdjustDown(php->a, php->size, 0);
}
判斷堆是否為空
當size為0時,堆即為空。
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
求堆中有幾個元素
size標記的就是有幾個元素。
//求堆中有幾個元素
size_t HeapSize(HP* php)
{
assert(php);
return php->size;
}
得到堆頂的值
需要註意的是size最少為1.當size為0時,就意味著堆已經為空。所以我們需要assert斷言size不為0.
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
堆排序
堆排序即利用堆的思想來進行排序,總共分為兩個步驟:
建堆
升序:建大堆
降序:建小堆(我們這裡用的是建小堆)利用堆刪除思想來進行排序
void HeapSort(HPDataType* a, int size)
{
HP hp;
HeapInit(&hp);
//先創建一個小堆
for (int i = 0; i < size; i++)
{
HeapPush(&hp, a[i]);
}
size_t j = 0;
//利用堆刪除思想來進行排序
while (!HeapEmpty(&hp))
{
a[j] = HeapTop(&hp);
j++;
HeapPop(&hp);
}
HeapDestroy(&hp);
}
int main()
{
//對a數組進行排序
int a[] = { 4,2,7,8,5,1,0,6 };
HeapSort(a, sizeof(a) / sizeof(int));
for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
時間復雜度分析:
時間復雜度為O(N*logN)。比冒泡排序上升瞭一個檔次哦。
但是空間復雜度有待改進。
但是空間復雜度因為占用瞭一個數組所以是O(N)。
空間復雜度改進的話需要很多字來詳解。下篇博文繼續敘述。
總體代碼
Heap.h
#define _CRT_SECURE_NO_WARNINGS
#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
size_t size;
size_t capacity;
}HP;
//初始化結構體
void HeapInit(HP* php);
//銷毀結構體
void HeapDestroy(HP* php);
//向堆裡插入數據
void HeapPush(HP* php, HPDataType x);
//交換堆中父子
void HeapSwap(HPDataType* pa, HPDataType* pb);
//刪除堆頂數據
void HeapPop(HP* php);
//按照下標打印堆
void HeapPrint(HP* php);
//判斷堆是否為空
bool HeapEmpty(HP* php);
//求堆中有幾個元素
size_t HeapSize(HP* php);
//得到堆頂的值
HPDataType HeapTop(HP* php);
Heap.c
#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
//初始化結構體
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
//銷毀結構體
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
//交換
void HeapSwap(HPDataType* pa, HPDataType* pb)
{
HPDataType tmp = *pa;
*pa = *pb;
*pb = tmp;
}
//向上調整
void AdjustUp(HPDataType* a, size_t child)
{
size_t parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
HeapSwap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//插入堆
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType)* newcapacity);
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size] = x;
++php->size;
//向上調整
AdjustUp(php->a, php->size - 1);
}
//向下調整
AdjustDown(HPDataType* a,size_t size, size_t root)
{
size_t parent= root;
size_t child= parent * 2 + 1;
while (child < size)
{
if (child+1 < size && a[child + 1] < a[child])
{
++child;
}
if (a[child] < a[parent])
{
HeapSwap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//刪除堆的值
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
//交換堆頂和堆尾的值。然後刪除堆尾的值
HeapSwap(php->a, &php->a[php->size - 1]);
--php->size;
//向下調整
AdjustDown(php->a, php->size, 0);
}
//打印堆
void HeapPrint(HP* php)
{
assert(php);
for (size_t i = 0; i < php->size; ++i)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
//判斷堆是否為空
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
//求堆中有幾個元素
size_t HeapSize(HP* php)
{
assert(php);
return php->size;
}
//得到堆頂的值
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
Test.c
#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
void testHeap()
{
HP hp;
HeapInit(&hp);
HeapPush(&hp, 5);
HeapPush(&hp, 4);
HeapPush(&hp, 3);
HeapPush(&hp, 2);
HeapPush(&hp, 1);
HeapPrint(&hp);
/*HeapPop(&hp);
HeapPrint(&hp);*/
HeapDestroy(&hp);
}
void HeapSort(HPDataType* a, int size)
{
HP hp;
HeapInit(&hp);
for (int i = 0; i < size; i++)
{
HeapPush(&hp, a[i]);
}
size_t j = 0;
while (!HeapEmpty(&hp))
{
a[j] = HeapTop(&hp);
j++;
HeapPop(&hp);
}
HeapDestroy(&hp);
}
int main()
{
/*testHeap();*/
int a[] = { 4,2,7,8,5,1,0,6 };
HeapSort(a, sizeof(a) / sizeof(int));
for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
以上就是C語言植物大戰數據結構二叉樹堆的詳細內容,更多關於C語言二叉樹堆的資料請關註LevelAH其它相關文章!