C++超詳細分析優化排序算法之堆排序
堆排序,學習瞭整整一天才把這個排序徹底搞明白……
首先第一點,堆排序是直接選擇排序的一種優化排序算法。由於直接排序算法的遍歷次數過多,導致直接排序算法的時間復雜度為O(N^2),不適合排大量數據,堆排序應運而生。
堆排序(Heap Sort)進行的改進是能夠保存一部分在每次遍歷整個數組找出最大(小)值、次大(小)值,主要利用的就是完全二叉樹這種數據結構。(後面說是如何保存這些數據的)
堆排序最重要的知識點無非兩個:
1、向下調整算法
2、堆的邏輯結構是一棵完全二叉樹
先從定義開始學習:
向下調整算法:顧名思義就是從上到下進行數據的調整,可以將完全二叉樹調整為最大堆與最小堆(這兩種堆也同時被稱為“大頂堆”和“小頂堆”)這種算法的前提是:根節點的左右兩棵子樹均以建成最大(小)堆。
最大堆:所有的父節點都大於子結點
最小堆:所有的父節點都小於子結點
完全二叉樹:從上到下、從左到右依次排列的一種樹(即從第一層到第n-1層都是滿的,隻有第n層不滿且從左到右排列數據)
(以建小堆為例)看一種典型的示例:

向下調整算法就是處理這種完全二叉樹的一種算法,經過這種算法可將此數組建成最小堆。
先從根節點開始處理:
9 為父(根)節點,0,1都是其子節點,0 < 1;所以將0與9作一次交換;父節點同時下移至子節點,子節點變為新父節點的子節點:(p = parent, c = child)

9 為父(根)節點,2,3都是其子節點,2 < 3;所以將2與9作一次交換;父節點同時下移至子節點,子節點變為新父節點的子節點:
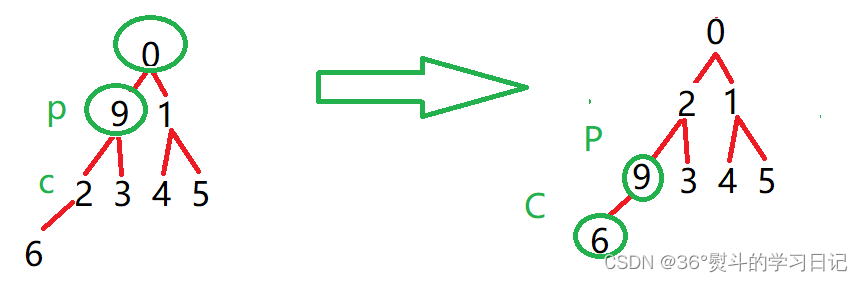
9 為父(根)節點,6 是其子節點,6< 9;所以將6與9作一次交換;父節點同時下移至子節點,子節點變為新父節點的子節點:

發現此時新的子節點已經越界,故停止向下調整;整個堆現已完成建堆成為最小堆!
這便是所謂的“向下調整算法”。
瞭解瞭以上知識後,還得知道父節點與子結點的表示方法:
leftchild = parent * 2 + 1;
rightchild = parent * 2 + 2;
parent = (leftchild – 1) /2;
下面代碼實戰:
//向下調整:
//根節點左右子樹必須已經成堆
void AdjustDown(int a[], int n, int parent)
{
int child = parent * 2 + 1;
//左孩子不能越界
while (child < n)
{
//如果隻有左孩子,那就不用判斷兩個孩子的大小,直接判斷左孩子和父親的大小
if (child + 1 < n && a[child + 1] > a[child])
{
child++;
}
//向下調整
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
簡單的交換函數:
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
堆排序的思想現在已經有瞭雛形:
將一個數組想象成堆,建堆,然後將堆頂最大(小)值置於堆底作為有序數據,這時會新形成一個堆,比之前的堆少一個數據,並且隻有根節點的那棵小樹未成堆,左右子樹已形成大(小)堆,用一次向下調整算法即可將新堆再次建成最大(小)堆。
現在的問題是我們選擇建一個最大堆還是最小堆呢?
我們不妨假設建瞭最小堆,也即上面我們剛剛構建好的堆:
不難發現這樣是將最小值篩選出來,再向下調整,選出次小值,這樣一來會得到降序的一個數組,反之,若使用最大堆,會得到一個升序的數組。

我們建大堆來得到一個升序數組,現有此無序數組:
//數組
int a[] = { 5,9,6,1,7,2,0,4,3,8 };
//元素個數
int n = (int)sizeof(a) / sizeof(a[0]);
第一步就是建堆:
我們會發現:這樣“不聽話”的數組顯然不符合向下調整算法的前提條件,所以我們可以從這個數組中找能用這個算法的地方:從後向前去調整,最後一個葉子節點?一個數據,不需要調整;
最後一個父節點?他將會有0-2個子節點,而且隻有這三個數據,不管怎麼“不聽話”,這個最小單位會滿足“根的左右子樹成堆”的這個條件,下一次再將這個父節點-1,即可實現對前一個父節點進行向下調整,循環此步驟直至真正的根節點,這時整個數組會被建成最大堆。
void HeapSort(int a[], int n)
{
//建堆
int parent = (n - 1 - 1) / 2;
while (parent >= 0)
{
AdjustDown(a, n, parent);
parent--;
}
}
第二步就是排序:
建成堆後,我們需要進行數據的交換形成有序數據區。
void HeapSort(int a[], int n)
{
//建堆
int parent = (n - 1 - 1) / 2;
while (parent >= 0)
{
AdjustDown(a, n, parent);
parent--;
}
//已經成最大堆,不用再從最後一個父節點建堆
//每次隻用改變根節點的堆(根左右堆已為最大堆)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
堆排序完畢!
整個代碼分享:
#include <stdio.h>
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//向下調整:
//根節點左右子樹必須已經成堆
void AdjustDown(int a[], int n, int parent)
{
int child = parent * 2 + 1;
//左孩子不能越界
while (child < n)
{
//如果隻有左孩子,那就不用判斷兩個孩子的大小,直接判斷左孩子和父親的大小
if (child + 1 < n && a[child + 1] > a[child])
{
child++;
}
//向下調整
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int a[], int n)
{
int parent = (n - 1 - 1) / 2;
while (parent >= 0)
{
AdjustDown(a, n, parent);
parent--;
}
//已經成最大堆,不用再從最後一個父節點建堆
//每次隻用改變根節點的堆(根左右堆已為最大堆)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
void print(int* a, int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
int main()
{
int a[] = { 5,9,6,1,7,2,0,4,3,8 };
int n = (int)sizeof(a) / sizeof(a[0]);
HeapSort(a, n);
print(a, n);
return 0;
}
到此這篇關於C++超詳細分析優化排序算法之堆排序的文章就介紹到這瞭,更多相關C++堆排序內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!