基於C++詳解數據結構(附帶例題)
前言
應廣大支持者的要求,隨我自身學習之餘,肝數據結構,開車隻是暫時的,飆車才是認真的,數據結構開始瞭,本文用c++編寫,如果有不足的地方歡迎大傢補充
數據結構
通常情況下,精心選擇的數據結構可以帶來更高的運行或者存儲效率,這也是一個優秀的程序員必須掌握的一項基本功,無論你學哪個語言,又提到瞭語言,這裡在推銷一波如果你還在糾結到底哪門語言作為主語言的話可以看文末
本文我主要講解數據結構中的
- 線性表
- 棧與隊列
- 串
- 樹
- 圖
這也就包含瞭所有的數據結構瞭,那廢話不多說,我們開始吧!
線性表
首先它是線性的,就像線一樣,小時候都玩過牽著手並排走的遊戲,話說我都幾年沒有牽過女孩手瞭,當時我們可以知道自己前面的人和後面的人是誰,像有線一樣連在瞭一起
官方定義:零個或多個數據元素的有限序列
序列,有限是我們應該著重註意的地方,還是小朋友牽手,他是一個有限的序列,其中小朋友視為數據元素,,例子有很多:月份,星座,直系關系等等都是線性表
下面在拿我自己舉一個例子,
碼神—>18—>155*********0111—>西安
順序存儲
這一通操作下來相信大傢應該對線性表有一個基礎的瞭解瞭吧,接著我們回到上述的拉手問題中,話說年輕碼手當時喜歡一個女孩,我們姑且稱她為小苗吧,我就希望自己可以拉上小苗的手,首先我要找到她,然後重新站到小苗的身邊,這時線性表就發生瞭重排,但是啊,小苗不喜歡我,直接就出列瞭,所以又出現瞭刪除的操作,上面我們可以看出來,這個線性表的基操就有查找,插入,刪除瞭,秉承學著就練這的原則,我現在來幫大傢實現一下
#include <iostream>
#include <cstdio>
#include <string>
#include <string.h>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 10005;
const int mod = 7654321;
typedef int ElementType;
typedef struct Node
{
ElementType data[maxn];//元素
int last;//最後一個元素的下標
}*List;
/*typedef是類型定義的意思。typedef struct 是為瞭使用這個結構體方便。
具體區別在於:
若struct node{}這樣來定義結構體的話。在申請node 的變量時,需要這樣寫,struct node n;
若用typedef,可以這樣寫,typedef struct node {}NODE; 。在申請變量時就可以這樣寫,NODE n;
區別就在於使用時,是否可以省去struct這個關鍵字。*/
//初始化一個空表
List CreatList()
{
List L;
L = (List)new int();
//開辟一塊新空間
L->last = -1;
return L;
}
//查找
ElementType Search(List L, ElementType x)
{
int i = 0;
while (i <= L->last)
{
if (L->data[i] == x)
return i;
i++;
}
return -1;
}
//插入
bool Insert(List L, int position, ElementType x)
{
if (L->last == maxn - 1)
{
cout << "表已滿" << endl;
return false;
}
if (position<0 || position>L->last + 1)
{
cout << "位置不合法" << endl;
return false;
}
for (int i = L->last; i >= position; i--)
{
L->data[i + 1] = L->data[i];
}
L->data[position] = x;
L->last++;
return true;
}
//刪除
bool Delet(List L, int position)
{
if (position<0 || position>L->last)
{
cout << "位置不合法" << endl;
return false;
}
for (int i = position + 1; i <= L->last; i++)
{
L->data[i - 1] = L->data[i];
}
L->last--;
return true;
}
int main()
{
List L = CreatList();
Insert(L, 0, 1);
Insert(L, 1, 1);
Insert(L, 2, 2);
cout << L->data[0] << endl;
Delet(L, 1);
cout << L->data[1] << endl;
cout << Search(L, 2) << endl;
return 0;
}
我們來談一下優缺點吧,實際上也很明顯,比如我要找到小苗,一眼就能看到,但是當我要插入,或者小苗要出來時,變化的就是整個隊伍瞭,還有不太明顯的地方:當線性表長度不確定時,難以確定儲存空間的大學,還可能造成存儲空間的“碎片”,用new。
鏈式
上面我們說到順序存儲最大的缺點就是插入和刪除要動所有的元素,為瞭解決這個問題我們引出瞭鏈式存儲
總體思路就是讓相鄰的元素之間留夠空位置,可能實現有點困難,但是 換個思路就簡單多瞭,也就是不要考慮相鄰位置瞭,哪裡有空位置就插到哪裡,而隻是讓每個元素知道她下一個元素的位置,這樣做的話,我們可以在第一個元素時,就知道第二個元素的位置,從而再找到第三個元素的位置,有點像單線索的偵探遊戲,下面我們用代碼來看一下具體的實現步驟吧。
#include <iostream>
#include <cstdio>
#include <string>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long ll;
#define maxn 10005
#define mod 7654321
typedef int ElementType;
typedef struct Node
{
ElementType data;
Node *next;
}*List;
//求表長
int Length(List L)
{
List P = L;
int num = 0;
while (P)
{
P = P->next;
num++;
}
return num;
}
//查找
/*讀取,較順序存儲比較麻煩
1.聲明一個指針p指向鏈表的第一個節點,從1開始
2.當j<i時,就遍歷鏈表,讓p的指針向後移動,j++
3.若鏈表末尾為空,則說明第i個節點不存在
4.查找成功,返回p的數據*/
List Search(List L, ElementType x)
{
List P = L;
while (L)
{
if (L->data == x)
return P;
L = L->next;
}
return NULL;
}
//插入
/*
1.聲明一指針p指向鏈表頭,初始化從1開始
2.p向後移動
3.查找成功,插入
4.插入標準語句
s->next=p->next;
p->next=s
*/
bool Insert(List L, ElementType x, List P)
{
List tem, Pre;
/* 查找P的前一個結點 */
while (L)
{
if (L->next == P)
{
Pre = L;
break;
}
L = L->next;
}
if (Pre == NULL)//不成功
return false;
else
{
tem = (List)malloc(sizeof(Node));
tem->data = x;
tem->next = P->next;
Pre->next = tem;
return true;
}
}
//刪除
/*
類比於插入
刪除標準語句p->next=q->next
q中數據賦值給e
然後釋放q
*/
bool Delete(List L, List P)
{
List Pre, tem;
while (L)
{
if (L->next == P)
Pre = L;
L = L->next;
}
if (Pre == NULL)
return false;
else
{
Pre->next = P->next;
return true;
}
}
int main()
{
return 0;
}
小結
若線性表需要頻繁的查找,很少進行插入和刪除操作時,應該選用順序儲存結構。
若線性表需要頻繁的插入和刪除操作時,很少查找時,應該選用鏈表結構。
why?
從時間性能來考慮的話,查找:
順序結構O(1),單鏈表(N)
插入刪除
順序:平均移動一半的距離O(N)
單鏈表在找出位置的指針後,插入和刪除的時間復雜度僅為O(1)
從空間復雜度來看的話:
順序需要預分配存儲空間,,but數據是不確定的,分大浪費,分小上溢。
單鏈表不需要分配儲存空間,隻要有就可以分配,元素個數也不受限制
So,當數據大小不確定的時候,最好使用單鏈表,但是像一年12月,一周7天這種還是用順序存儲比較效率高一點。
棧和隊列
棧:僅在表尾進行插入和刪除操作的線性表
隊列:隻允許在一端進行插入,而在另一端進行刪除的線性表
棧
如果說棧最大特征應該就是:先進後出瞭,像以前的沙漠之鷹的彈夾一樣,先放入的子彈,後面才能打出
棧的應用在軟件中也比較普遍,像瀏覽器中的後退一樣單擊後可以按訪問順序的逆序加載瀏覽過的網頁

還有許多的文本編輯軟件的“ctrl+z”的撤銷功能,也是通過棧來實現的
瞭解瞭什麼是棧之後,我們來說棧的幾個概念
- 棧頂:允許插入和刪除的一端
- 棧底:棧頂的另一端
- 空棧:不含任何元素的
- 還可以說是棧是限定僅在表尾(棧頂)進行插入和刪除操作的線性表
- 插入就叫進棧
- 刪除稱為出棧
就像沙漠之鷹的彈夾一樣,進棧為子彈彈入彈夾,出棧為子彈彈出彈夾

看例題吧,嘗試一種新的寫法,用算法題來解決棧的問題,因為我感覺實現和線性表的差不多
鐵軌:uva514
某城市有一個火車站,鐵軌鋪設如圖。有n節車廂從A方向駛入車站,按進站的順序編號為1~n。你的任務是判斷是否能讓他們按照某種特定的順序進入B方向的鐵軌並駛出車站。例如,出棧順序(5 4 1 2 3)是不可能的,但(5 4 3 2 1)是可能的。 為瞭重組車廂,你可以借助中轉站C。這是一個可以停放任意多節車廂的車站,但由於末端封頂,駛入C的車廂必須按照相反的順序駛出C。對於每節車廂,一旦從A移入C,就不能返回A瞭;一旦從C移入B,就不能返回C瞭。也就是說,在任意時刻,隻有兩種選擇:A到C和C到B。
//首先中轉站C中,車廂符合先進後出的原則,是一個棧
#include<cstdio>
#include<stack>
using namespace std;
const int maxn = 1000 + 10;
int n, target[maxn];
int main()
{
while (scanf_s("%d", &n) == 1)
{
stack<int> s;
int a = 1, b = 1;
for (int i = 1; i <= n; i++)
{
scanf_s("%d", &target[i]);
}
int ok = 1;
while (b <= n)
{
if (a == target[b])
{
a++;
b++;
}
else if (!s.empty() && s.top() == target[b])
//運用empty和top函數,包含頭文件《stack》
{
s.pop();
b++;
}
else if (a <= n)
s.push(a++);
else
{
ok = 0;
break;
}
}
printf("%s\n", ok ? "yes" : "no");
}
return 0;
}
後綴表達式
提棧還是繞不開後綴表達式,我感覺我講的也不太好,看個b站視頻吧後綴表達式下面我用代碼實現一下
#include <iostream>
#include <stack>
using namespace std;
//表達式求值
const int MaxSize = 100;
void trans(char exp[], char postexp[])
{
stack<char> op;
int i = 0, j = 0;
//op.top = -1;
while (*exp != '\0')
{
switch (*exp)
{
case '('://左括號進棧
op.push(*exp);
exp++;
break;
case ')'://將棧中“(”以前的運算符依次刪除存入數組exp中,然後將“(”刪除
while (!op.empty() && op.top() != '(')
{
postexp[i++] = op.top();
op.pop();
}
op.pop();
exp++;
break;
case '+':
case '-':
while (!op.empty() && op.top() != '(')
{//將棧中優先級大於等於‘+'或'-'的運算符退棧並存放到postexp中
postexp[i++] = op.top();
op.pop();
}
op.push(*exp);
exp++;
break;
case '*':
case '/':
while (!op.empty() && (op.top() == '*' || op.top() == '/'))
{//將棧中的“*”或者是“/”運算符依次出棧並存放到postexp中
postexp[i++] = op.top();
op.pop();
}
op.push(*exp);
exp++;
break;
case ' ':break;
default:
while (isdigit(*exp))
{
postexp[i++] = *exp;
exp++;
}
postexp[i++] = '#';
}
}
while (!op.empty())//最後的掃描工作
{
postexp[i++] = op.top();;
op.pop();;
}
postexp[i] = '\0';
cout << "後綴表達式" << endl;
for (j = 0; j < i; j++)
{
if (postexp[j] == '#')
j++;
cout << postexp[j];
}
cout << endl;
}
float compvalue(char postexp[])
{
stack<float> st;
float a, b, c, d;
while (*postexp != '\0')
{
switch (*postexp)
{
case '+':
a = st.top();
st.pop();
b = st.top();;
st.pop();;
c = a + b;
st.push(c);
break;
case '-':
a = st.top();
st.pop();
b = st.top();;
st.pop();;
c = b - a;
st.push(c);
break;
case '*':
a = st.top();
st.pop();
b = st.top();;
st.pop();;
c = a * b;
st.push(c);
break;
case '/':
a = st.top();
st.pop();
b = st.top();;
st.pop();;
if (a != 0)
{
c = b / a;
st.push(c);
}
else
{
cout << "除零錯誤!" << endl;
exit(0);
}
break;
default://進行最後的掃尾工作,將數字字符轉換成數值存放到d中
d = 0;
while (isdigit(*postexp))
{
d = 10 * d + *postexp - '0';
postexp++;
}
st.push(d);
break;
}
postexp++;
}
return (st.top());
}
int main()
{
char exp[MaxSize] = "((18+6)*2-9)/2";
char postexp[MaxSize] = { 0 };
trans(exp, postexp);//exp存放中綴表達式,postexp存放後綴表達式
printf("後綴表達式的值\n");
printf("%.2f\n", compvalue(postexp));
return 0;
}
隊列
排隊?算瞭,用電腦來解釋吧,cpu就是一個隊列,一個執行完再到下一個,和隊列一樣先進先出也符合生活習慣,排在前面的優先出列
隊列的專業術語和棧差不多類比吧
- 隊頭
- 隊尾
- 出隊
- 入隊
下面我們來實現一下隊列,還是用算法題來吧
排隊
一個學校裡老師要將班上NN個同學排成一列,同學被編號為1\sim N1∼N,他采取如下的方法:
- 先將11號同學安排進隊列,這時隊列中隻有他一個人;
- 2−N號同學依次入列,編號為i的同學入列方式為:老師指定編號為i的同學站在編號為1\sim (i -1)1∼(i−1)中某位同學(即之前已經入列的同學)的左邊或右邊;
- 從隊列中去掉M(M<N)M(M<N)個同學,其他同學位置順序不變。
在所有同學按照上述方法隊列排列完畢後,老師想知道從左到右所有同學的編號。
先分析:因為n還是比較大的(n<=100000),又因為要不停的插入和刪除,所以我們可以用鏈表。讀入每一個同學時,都把他左邊和右邊的同學更新;刪除同學時,先把這個同學賦為0,再把他左邊的同學連上右邊的同學;最後找到排在最左邊的同學,挨個輸出。時間復雜度O(n)。
#include<cstdio>
#include<cstring>
int a[100010][3],n,m;
//a[i][2]表示學號為i的同學右邊同學的學號
//a[i][3]表示學號為i的同學左邊同學的學號
int main()
{
scanf("%d",&n);
int j=1;
memset(a,0,sizeof(a));
a[1][1]=1;
for(int i=2;i<=n;i++)
{
int x,y; scanf("%d %d",&x,&y);
a[i][1]=i;
if(y==0)
//插入左邊
{
a[a[x][3]][2]=i; a[i][2]=x;
a[i][3]=a[x][3]; a[x][3]=i;
if(x==j) j=i;
//比較麻煩,要改鏈表
}
else
//插入右邊
{
a[i][2]=a[x][2]; a[a[x][2]][3]=i;
a[x][2]=i; a[i][3]=x;
}
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
int x; scanf("%d",&x);
if(a[x][1]!=0)
//該同學還在
{
a[x][1]=0;
//踢掉
a[a[x][3]][2]=a[x][2];
a[a[x][2]][3]=a[x][3];
n--;
if(x==j) j=a[x][3];
}
}
int i=1,x=j;
while(i<=n)
{
printf("%d ",a[x][1]);
x=a[x][2]; i++;
}
return 0;
}
還有就是隊列是隻允許在一端進行插入操作,而在另一端進行刪除操作的線性表
棧是僅在表尾(棧頂)進行插入和刪除操作的線性表
又想起瞭我入門時候的一首小詩——來自大話數據結構
人生,就像是一個很大的棧演變。 出生時你赤條條地來到人世,慢慢地長大,漸浙地變老,最終還得赤條條地離開世間。
人生,又仿佛是一天一天小小的棧重現。童年父母每天抱你不斷地進出傢門,壯年你每天奔波於傢與事業之間,老年你每天獨自蹣珊於養老院的門裡屋前。
人生,更需要有進棧出棧精神的體現。在哪裡跌倒,就應該在哪裡爬起來。無論陷入何等困境,隻要抬頭能仰望藍天,就有希望,不斷進取,你就可以讓出頭之日重現。困難不會永遠存在,強者才能勇往直前。
人生,其實就是一個大大的隊列演變。無知童年、快樂少年,稚傲青年,成熟中年,安逸晚年。
人生,又是一個又一個小小的隊列重現。春夏秋冬輪回年,早中晚夜循環天天。變化的是時間,不變的是你對未來執著的信念。
人生,更需要有隊列精神的體現。南極到北極,不過是南緯90º到北緯90º的隊列,如果你中逢猶豫,臨時轉向,也許你就隻能和企鵝相伴永遠。可事實上,無論哪個方向,隻要你堅持到底,你都可以到達終點。
好瞭感慨完,該開串瞭
串
串:由零個或多個字符串組成的有限序列,又稱字符串
我打算就分倆個方面講解
- 串的基本使用
- kmp算法
串的基本用法
串一般記為 s="absd"其中s是串的名字,c++中用雙引號擴展起來的是串的內容,雙引號不屬於串的內容
還有幾個概念:
- 空格串:區別於空串,空格串是有內容有長度的,隻是都是空格,但是空串沒有內容
- 子串與主串:串中任意個數的連續字符組成的子序列稱為該串的子串,包含子串的串稱為主串
像Lover中的over就是主串與子串的關系
ASCII碼
在計算機中,所有的數據在存儲和運算時都要使用二進制數表示(因為計算機用高電平和低電平分別表示1和0),例如,像a、b、c、d這樣的52個字母(包括大寫)以及0、1等數字還有一些常用的符號(例如*、#、@等)在計算機中存儲時也要使用二進制數來表示,而具體用哪些二進制數字表示哪個符號,當然每個人都可以約定自己的一套(這就叫編碼),而大傢如果要想互相通信而不造成混亂,那麼大傢就必須使用相同的編碼規則,於是美國有關的標準化組織就出臺瞭ASCII編碼,統一規定瞭上述常用符號用哪些二進制數來表示
在c++中char字符型變量,一個變量對應一個ascll碼值

串的基本實現
實話實話,我感覺串的邏輯結構和線性表的很類似,不同之處是串針對的是字符集,但是代碼實現還是有些不同之處,比如:查找

這就是一個串的查找,可以看到它自動給我補齊的操作,這也與之後的kmp算法有關
現在我先來用簡單的傻瓜式搜索實現一下所有代碼
//在c中許多是要單獨寫的,但是c++引入瞭string,其中包含瞭許多函數就不用自己直接寫瞭,為瞭學習我先用c寫,之後講解c++的string
#include <iostream>
#include <string>
using namespace std;
int main ()
{
int size = 0;
int length = 0;
unsigned long maxsize = 0;
int capacity=0;
string str ("12345678");
string str_custom;
str_custom = str;
str_custom.resize (5);
size = str_custom.size();//大小
length = str_custom.length();//長度
cout << "size = " << size << endl;
cout << "length = " << length << endl;
return 0;
}
傻瓜模式匹配算法
int i = pos;
int j = 1;
while (i <= s[0] && j <= t[0])//當i<s的長度,且j<t的長度,循環繼續
{
if (s[i] = t[j])
{
i++;
j++;//繼續
}
else//缺點:後退重新匹配
{
i = i - j + 2;//i回到上次匹配首位的下一位
j = 1;//回到首位
}
}
if (j > t[0])
return i - t[0];//不匹配
else
return 0;
利用入門知識分析一下吧,最好的情況下,最好的結果是O(m),最壞的結果是O(n+m),取個平均是(n+m)/2,時間復雜度是O(n+m)
那麼最壞的情況?就是每次不匹配成功都發生在串s,的最後一個字節上,這樣的話,時間復雜度就成瞭O((n-m+1)*m)
KMP模式算法匹配
模式匹配的算法雖然簡單但是實際上是非常糟糕的,實際上和算法中的動態規劃有點像,動態規劃就是減少瞭重復的計算,來換取高效,這裡的kmp也一樣,分析我們不難發現,模式匹配算法主要就是重復匹配太多瞭,kmp減少瞭重復的匹配來實現高效
正題:KMP算法是怎樣優化這些步驟的。其實KMP的主要思想是:“空間換時間”,也和dp一樣
首先,為什麼樸素的模式匹配這麼慢呢?
你再回頭看一遍就會發現,哦,原來是回溯的步驟太多瞭。所以我們應該盡量減少回溯的次數。
怎樣做呢?比如:goodgoole當字符’d’與’g’不匹配,我們保持主串的指向不變,

主串依然指向’d’,而把子串進行回溯,讓’d’與子串中’g’之前的字符再進行比對。
如果字符匹配,則主串和子串字符同時右移。
上代碼吧,作圖能力實在不行,如果沒有看明白,還請評論,我再講解
typedef struct
{
char data[MaxSize];
int length; //串長
} SqString;
//SqString 是串的數據結構
//typedef重命名結構體變量,可以用SqString t定義一個結構體。
void GetNext(SqString t,int next[]) //由模式串t求出next值
{
int j,k;
j=0;k=-1;
next[0]=-1;//第一個字符前無字符串,給值-1
while (j<t.length-1)
//因為next數組中j最大為t.length-1,而每一步next數組賦值都是在j++之後
//所以最後一次經過while循環時j為t.length-2
{
if (k==-1 || t.data[j]==t.data[k]) //k為-1或比較的字符相等時
{
j++;k++;
next[j]=k;
//對應字符匹配情況下,s與t指向同步後移
//通過字符串"aaaaab"求next數組過程想一下這一步的意義
//printf("(1) j=%d,k=%d,next[%d]=%d\n",j,k,j,k);
}
else
{
k=next[k];
**//我們現在知道next[k]的值代表的是下標為k的字符前面的字符串最長相等前後綴的長度
//也表示該處字符不匹配時應該回溯到的字符的下標
//這個值給k後又進行while循環判斷,此時t.data[k]即指最長相等前綴後一個字符**
//為什麼要回退此處進行比較,我們往下接著看。其實原理和上面介紹的KMP原理差不多
//printf("(2) k=%d\n",k);
}
}
}
//kmp
int KMPIndex(SqString s,SqString t) //KMP算法
{
int next[MaxSize],i=0,j=0;
GetNext(t,next);
while (i<s.length && j<t.length)
{
if (j==-1 || s.data[i]==t.data[j])
{
i++;j++; //i,j各增1
}
else j=next[j]; //i不變,j後退,現在知道為什麼這樣讓子串回退瞭吧
}
if (j>=t.length)
return(i-t.length); //返回匹配模式串的首字符下標
else
return(-1); //返回不匹配標志
}
算瞭算瞭,這樣我都有點暈
看算法題目吧
kmp字符串匹配


#include<iostream>
#include<cstring>
#define MAXN 1000010
using namespace std;
int kmp[MAXN];
int la,lb,j;
char a[MAXN],b[MAXN];
int main()
{
cin>>a+1;
cin>>b+1;
la=strlen(a+1);
lb=strlen(b+1);
for (int i=2;i<=lb;i++)
{
while(j&&b[i]!=b[j+1])
j=kmp[j];
if(b[j+1]==b[i])j++;
kmp[i]=j;
}
j=0;
for(int i=1;i<=la;i++)
{
while(j>0&&b[j+1]!=a[i])
j=kmp[j];
if (b[j+1]==a[i])
j++;
if (j==lb) {cout<<i-lb+1<<endl;j=kmp[j];}
}
for (int i=1;i<=lb;i++)
cout<<kmp[i]<<" ";
return 0;
}
其實我們也可以發現, KMP算法之所以快,不僅僅由於它的失配處理方案,更重要的是利用前綴後綴的特性,從不會反反復復地找,我們可以看到代碼裡對於匹配隻有一重循環,也就是說 KMP 算法具有一種“最優歷史處理”的性質,而這種性質也是基於 KMP的核心思想的。
樹
終於擺脫線性表瞭,線性表是一對一,但是樹就不一樣瞭,一對多的性質撲面而來,先看一下百度的說法吧,
樹:它是由n(n≥1)個有限節點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。

就用這張圖來描述樹的特征:
- 當n=0,就稱為空樹
- 有且隻有一個稱為根的結點,這裡為A
- 當n>1時,其餘結點可以分為m(m>0)個互不相交的有限集,其中每個集合又是一棵樹,稱為子樹
舉個例子:

是以B為結點的子樹
下面我們來將結點分一下類:
- 樹的結點包含一個數據結構及若幹指向其子樹的分支
- 結點擁有的子樹稱為結點的度
- 度為0的結點稱為葉結點或終端結點
- 度不為0的結點稱為非終端結點或分支結點
看圖

結點的關系:
這塊有點像我們的傢庭關系,比較好理解
像上圖A為B,C的雙親,B,C互為兄弟,對於#來說,D,B,A,都是它的祖先,反之A的子孫有B,D,#
其他相關概念,特定情況才會用到

引入瞭深度,可以說是有幾層就有多少深度.
無序樹:如果將樹中結點的各子樹看成從左到右都是沒有次序,都可以隨意互換,則稱為無序樹,反之為有序樹
樹的基本操作
雙親表示法
樹真的太像人瞭,人可能暫時沒有孩子但是一定有且隻有一個父母,樹也一樣除瞭根結點外,其餘每個結點,它不一定有孩子,但是一定有且隻有一個雙親
/*
Project: Tree_parent(樹-雙親表示法)
Date: 2019/02/25
Author: Frank Yu
基本操作函數:
InitTree(Tree &T) 參數T,樹根節點 作用:初始化樹,先序遞歸創建
InsertNode(Tree &T, TElemType node) 插入樹的結點 參數:樹T,結點node 作用:在雙親數組中插入結點,增加樹的結點值
InsertParent(Tree &T, TElemType node1, TElemType node2)//插入雙親數組的雙親域 參數:樹T ,結點node1,結點node2
//作用:使雙親數組中,node2對應的雙親域為node1的下標
GetIndegree(Tree &T, TElemType node) //得到某結點入度 參數:樹T,結點node 結點不存在返回-1
GetOutdegree(Tree &T, TElemType node) //得到某結點出度 參數:樹T,結點node 結點不存在返回-1
PreOrder(Tree T) 參數:樹T,根節點下標 作用:先序遍歷樹
PostOrder(Tree T) 參數:樹T,根節點下標 作用:後序遍歷樹
LevelOrder(Tree T)參數:樹T 作用:層序遍歷樹
功能實現函數:
CreateTree(Tree &T) 參數T,樹根節點 作用:創建樹,調用InsertNode,InsertParent
Traverse(Tree T) 參數T,樹根節點 作用:PreOrder InOrder PostOrder LevelOrder遍歷樹
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<string>
#include<stack>
#include<queue>
#include<algorithm>
#include<iostream>
#define TElemType char
#define Max 100
using namespace std;
//樹的結點數據結構
typedef struct TNode
{
TElemType data;//數據域
int parent; //雙親
}TNode;
//樹的數據結構
typedef struct Tree
{
TNode parent[Max];
int NodeNum;
}Tree;
//********************************基本操作函數********************************//
//初始化樹函數 參數:樹T 作用:規定數據域為#,則為空,雙親為-1,則為空
void InitTree(Tree &T)
{
for (int i=0;i<Max;i++)
{
T.parent[i].data = '#';
T.parent[i].parent = -1;
}
T.NodeNum = 0;
}
//插入樹的結點 參數:樹T,結點node 作用:在雙親數組中插入結點,增加樹的結點值
bool InsertNode(Tree &T, TElemType node)
{
if (node != '#')
{
T.parent[T.NodeNum++].data = node;//插入到雙親數組中
return true;
}
return false;
}
//插入雙親數組的雙親域 參數:樹T ,結點node1,結點node2
//作用:使雙親數組中,node2對應的雙親域為node1的下標
bool InsertParent(Tree &T, TElemType node1, TElemType node2)
{
int place1, place2;
place1 = -1;place2 = -1;
for (int i=0;i<T.NodeNum;i++)//查找兩點是否存在
{
if (node1 == T.parent[i].data)place1 = i;
if (node2 == T.parent[i].data)place2 = i;
}
if (place1 != -1 && place2 != -1)//兩點均存在
{
T.parent[place2].parent = place1;
return true;
}
return false;
}
//得到某結點入度 參數:樹T,結點node 結點不存在返回-1
int GetIndegree(Tree &T, TElemType node)
{
int place = -1;
for (int i = 0;i<T.NodeNum;i++)
{
if (T.parent[i].data == node)place = i;
}
if (place!=-1)//結點存在
{
if(T.parent[place].parent!=-1)return 1;//雙親隻能有一個
else return 0; //根節點沒有雙親,即沒有入度
}
return -1;
}
//得到某結點出度 參數:樹T,結點node 結點不存在返回-1
int GetOutdegree(Tree &T, TElemType node)
{
int place = -1;
int outdegree = 0;
for (int i = 0;i<T.NodeNum;i++)
{
if (T.parent[i].data == node)place = i;
}
if (place != -1)
{
for (int i = 0;i < T.NodeNum;i++)
{
if (T.parent[i].parent == place)outdegree++;
}
return outdegree;
}
return -1;
}
//先序遍歷 參數:樹T,根節點下標
void PreOrder(Tree T,int i)
{
if (T.NodeNum != 0)
{
cout << T.parent[i].data << " ";
for(int j=0;j<T.NodeNum;j++)
{
if(T.parent[j].parent==i)
PreOrder(T,j);//按左右先序遍歷子樹
}
}
}
//後序遍歷 參數:樹T,根節點下標
void PostOrder(Tree T,int i)
{
if (T.NodeNum != 0)
{
for (int j = 0;j<T.NodeNum;j++)
{
if (T.parent[j].parent == i)
PostOrder(T, j);//按左右先序遍歷子樹
}
cout << T.parent[i].data << " ";
}
}
//層序遍歷 參數:樹T
void LevelOrder(Tree T)
{
queue<TNode> q;//借助隊列
if (T.NodeNum!=0)
{
TNode temp;//暫存要出隊的結點
q.push(T.parent[0]);//根結點入隊
while (!q.empty())//隊列非空
{
temp = q.front();
q.pop();
cout<<temp.data<<" ";
for (int j = 0;j<T.NodeNum;j++)
{
if (T.parent[T.parent[j].parent].data == temp.data)//當前結點的父節點的數據域與彈出的相同
//因為temp沒有保存下標,隻能按這種方式比較,默認結點名稱不同
q.push(T.parent[j]);//隊列先進先出,先入左孩子
}
}
}
}
//**********************************功能實現函數*****************************//
//創建樹,調用InsertNode,InsertParent
void CreateTree(Tree &T)
{
int nodenum = 0;
int parent;
TElemType node,node1,node2;
printf("請輸入樹的結點個數:");
cin >> nodenum;
parent = nodenum - 1;
printf("請輸入樹的結點名稱(空格隔開):");
while (nodenum--)
{
cin >> node;
InsertNode(T,node);
}
printf("請輸入樹的結點間的雙親關系(一對為一雙親關系,A B表示A為B的雙親):\n");
while (parent--)
{
cin >> node1>>node2;
InsertParent(T,node1,node2);
}
printf("\n");
}
//入度
void Indegree(Tree &T)
{
TElemType node;
int indegree;
printf("請輸入結點名稱:\n");
cin >> node;
indegree = GetIndegree(T, node);
if (-1 != indegree)
cout << "該結點入度為:" << indegree << endl;
else
cout << "結點不存在。" << endl;
}
//出度
void Outdegree(Tree &T)
{
TElemType node;
int outdegree;
printf("請輸入結點名稱:\n");
cin >> node;
outdegree = GetOutdegree(T, node);
if (-1 != outdegree)
cout << "該結點出度為:" << outdegree << endl;
else
cout << "結點不存在。" << endl;
}
//遍歷功能函數 調用PreOrder InOrder PostOrder LevelOrder
void Traverse(Tree T)
{
int choice;
while (1)
{
printf("********1.先序遍歷 2.後序遍歷*********\n");
printf("********3.層次遍歷 4.返回上一單元*********\n");
printf("請輸入菜單序號:\n");
scanf("%d", &choice);
if (4 == choice) break;
switch (choice)
{
case 1: {printf("樹先序遍歷序列:");PreOrder(T,0);printf("\n");}break;
case 2: {printf("樹後序遍歷序列:");PostOrder(T,0);printf("\n");}break;
case 3: {printf("樹層序遍歷序列:");LevelOrder(T);printf("\n");}break;
default:printf("輸入錯誤!!!\n");break;
}
}
}
//菜單
void menu()
{
printf("********1.創建 2.某點入度*********\n");
printf("********3.某點出度 4.遍歷*************\n");
printf("********5.退出\n");
}
//主函數
int main()
{
Tree T;
int choice = 0;
InitTree(T);
while (1)
{
menu();
printf("請輸入菜單序號:\n");
scanf("%d", &choice);
if (5 == choice) break;
switch (choice)
{
case 1:CreateTree(T);break;
case 2:Indegree(T);break;
case 3:Outdegree(T);break;
case 4:Traverse(T);break;
default:printf("輸入錯誤!!!\n");break;
}
}
return 0;
}
所用圖

孩子表示法
顧名思義,就是每個結點有多個指針域,其中每個指針指向一棵子樹的根結點,我們也把這種方法叫做多重鏈表表式法,有點像線性表中的鏈式表示法
那麼這樣的話,我這裡就寫偽代碼瞭
//指針域的個數就等於樹的度,其中樹的度又等於樹各個結點度的最大值
struct ChildNode
{
int data;
ChildNode*;
}
ChildNode *D;//d為最大結點
d.ChildNode;
不難看出這樣的話,如果各個樹度之間的差距不大,還可以,但是如果各個樹度之間的差距很大,那麼很浪費空間,原因是許多的結點域都是空的

孩子兄弟表示法
這個可以說是學二叉樹的基礎,有的兄弟可能要說瞭,為什麼不是兄弟表示法?還要帶上我的孩子一起?
因為可能存在下面這種情況,隻有瞭兄弟,孩子沒有辦法往下延申瞭,那麼如何孩子和兄弟一起開呢?
是這樣的,任意一棵樹,它的結點的第一個孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的,記得不是堂兄弟昂,是親兄弟,下面我們
看圖


觀察後,我們可以發現每個結點最多有倆個孩子,也就是一個簡單的二叉樹,這也可以說是,孩子兄弟表示法最大的好處
struct Node
{
int data;
*firstchild,*ringtsib;
}
Node *Tree;
二叉樹
惡魔來瞭,有關二叉樹及其衍生的東西往往是樹中的難點,下面來個大傢講個故事:還是以前的小苗,話說我以前剛看上小苗時,幾乎沒有人知道,但是我對我的兄弟說我看上瞭一個女孩,讓他猜,但是我每次隻回答”對“或”錯“,然後就相當於降低瞭難度莫,身高,體重,魅力,頭發等等,都可以用一個人來比較,這樣的話又降低瞭難度,二叉樹也是一樣的,隻不過它是通過比較大小來降低難度的,下面我們回歸正題
特點:
- 每個結點最多有倆棵子樹
- 左右子樹都是有順序的,不能任意顛倒
- 即使隻有一棵子樹,也要區分它是左子樹還是右子樹
一般情況下,有以下幾種基本形態
空二叉樹,沒有辦法畫圖瞭
隻有一個根結點

根結點隻有左子樹

根結點隻有右子樹

根結點既有左子樹又有右子樹

再思考一下,如果有三個結點的二叉樹,又有幾種形態呢?
5種,怎麼來的?先看圖
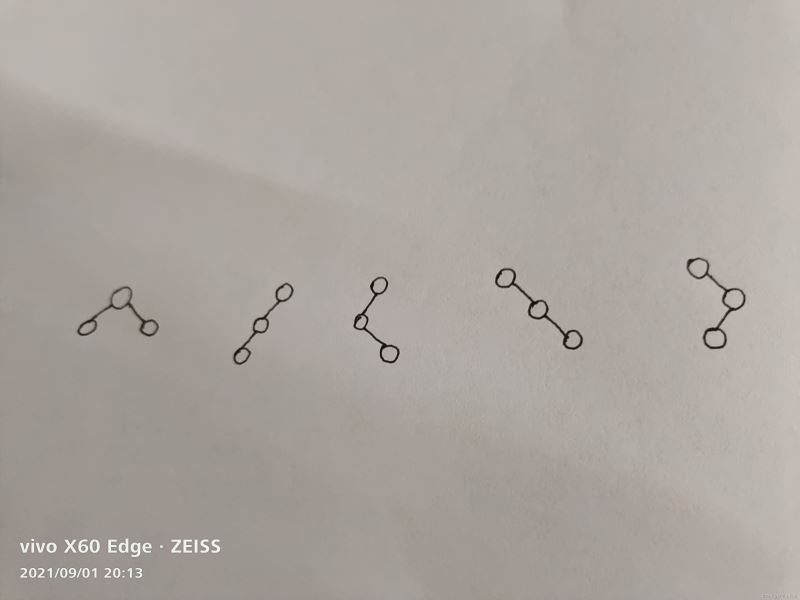
由於他必須是有序的所以要單個計算,左右分開,加起來就是5種
下面來說幾個特殊的二叉樹:
滿二叉樹:一個二叉樹,如果每一個層的結點數都達到最大值,則這個二叉樹就是滿二叉樹。也就是說,如果一個二叉樹的層數為K,且結點總數是(2^k) -1 ,則它就是滿二叉樹。
完全二叉樹:完全二叉樹是效率很高的數據結構,完全二叉樹是由滿二叉樹而引出來的。對於深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。 要註意的是滿二叉樹是一種特殊的完全二叉樹。
斜樹:有點像線性表,這個斜可以不分左右,所以更像線性表瞭
如何判斷完全二叉樹,下面是它的特征:
- 葉子結點隻能出現在最下倆層、
- 最下層的葉子一定集中在左部的連續位置
- 倒數倆層,若有葉子結點,一定都在右部連續位置
- 如果結點度為一,則該結點隻有左孩子
- 同樣結點數的二叉樹,完全二叉樹的深度最小
下面我們來看一下,二叉樹的存儲結構吧,也分為順序存儲和鏈式存儲
順序存儲
由於樹是一對多的關系,順序存儲實現有點困難,但是二叉樹是一種特殊的樹,由於它的特殊性,順序存儲可以實現。
順序結構存儲就是使用數組來存儲,一般使用數組隻適合表示完全二叉樹,因為不是完全二叉樹會有空間的浪費。而現實中使用中隻有堆才會使用數組來存儲。二叉樹順序存儲在物理上是一個數組,在邏輯上是一顆二叉樹。
鏈表存儲
由於二叉樹每個結點最多有倆個孩子,所以給它設計一個數據域和倆個指針域,組成二叉鏈表
struct BinaryTreeNode
{
struct BinTreeNode* _pLeft; // 指向當前節點左孩子
struct BinTreeNode* _pRight; // 指向當前節點右孩子
BTDataType _data; // 當前節點值域
}
BinaryTreeNode *tree;

遍歷二叉樹
所謂遍歷(Traversal)是指沿著某條搜索路線,依次對樹中每個結點均做一次且僅做一次訪問。訪問結點所做的操作依賴於具體的應用問題。從而引出瞭次序問題,像碼神剛剛結束的高考志願問題,哪個城市,哪個學校,哪個專業,或者那個她,由於選擇不同,所以最後的遍歷次序也截然不同。
方法:
- 前序遍歷——訪問根結點的操作發生在遍歷其左右子樹之前。
從根開始先左後右 - 中序遍歷——訪問根結點的操作發生在遍歷其左右子樹之中。
中序遍歷根結點的左子樹,然後是訪問根結點,最後中序遍歷右子樹 - 後序遍歷——訪問根結點的操作發生在遍歷其左右子樹之後。
從左到右先子葉後結點的方式遍歷訪問左右子樹,最後是根結點 - 層序遍歷——設二叉樹的根節點所在層數為1,層序遍歷就是從所在二叉樹的根節點出發,首先訪問第一層的樹根節點,然後從左到右訪問第2層上的節點,接著是第三層的節點,以此類推,自上而下,自左至右逐層訪問樹的結點的過程就是層序遍歷。
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
typedef BTNode* QDataType;
// 鏈式結構:表示隊列
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 隊列的結構
typedef struct Queue
{
QNode* _front;
QNode* _rear;
}Queue;
BTNode* CreateBTNode(BTDataType x);
// 通過前序遍歷的數組"ABD##E#H##CF##G##"構建二叉樹
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉樹銷毀
void BinaryTreeDestory(BTNode** root);
// 二叉樹節點個數
int BinaryTreeSize(BTNode* root);
// 二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root);
// 二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉樹前序遍歷
void BinaryTreePrevOrder(BTNode* root);
// 二叉樹中序遍歷
void BinaryTreeInOrder(BTNode* root);
// 二叉樹後序遍歷
void BinaryTreePostOrder(BTNode* root);
// 初始化隊列
void QueueInit(Queue* q);
// 隊尾入隊列
void QueuePush(Queue* q, QDataType data);
// 隊頭出隊列
void QueuePop(Queue* q);
// 獲取隊列頭部元素
QDataType QueueFront(Queue* q);
// 獲取隊列隊尾元素
QDataType QueueBack(Queue* q);
// 獲取隊列中有效元素個數
int QueueSize(Queue* q);
// 檢測隊列是否為空,如果為空返回非零結果,如果非空返回0
int QueueEmpty(Queue* q);
// 銷毀隊列
void QueueDestroy(Queue* q);
// 層序遍歷
void BinaryTreeLevelOrder(BTNode* root);
// 判斷二叉樹是否是完全二叉樹
int BinaryTreeComplete(BTNode* root);
// 初始化隊列
void QueueInit(Queue* q)
{
assert(q);
q->_front = q->_rear = NULL;
}
// 隊尾入隊列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode *newnode = ((QNode*)malloc(sizeof(QNode)));
newnode->_data = data;
newnode->_next = NULL;
if (q->_rear == NULL)
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
//q->_rear = q->_rear->_next;
q->_rear = newnode;
}
}
// 隊頭出隊列
void QueuePop(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
if (q->_front == q->_rear)
{
free(q->_front);
//free(q->_rear);
q->_front = q->_rear = NULL;
}
else
{
QNode *cur = q->_front->_next;
free(q->_front);
q->_front = cur;
}
}
// 獲取隊列頭部元素
QDataType QueueFront(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->_front->_data;
}
// 獲取隊列隊尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->_rear->_data;
}
// 獲取隊列中有效元素個數
int QueueSize(Queue* q)
{
assert(q);
int size = 0;
QNode* cur = q->_front;
while (cur)
{
++size;
cur = cur->_next;
}
return size;
}
// 檢測隊列是否為空,如果為空返回非零結果,如果非空返回0
int QueueEmpty(Queue* q)
{
assert(q);
return q->_front == NULL ? 1 : 0;
}
// 銷毀隊列
void QueueDestroy(Queue* q)
{
assert(q);
QNode *cur = q->_front;
while (cur)
{
QNode *next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_rear = NULL;
}
BTNode* CreateBTNode(BTDataType x)
{
BTNode *node = (BTNode*)malloc(sizeof(BTNode));
node->_data = x;
node->_left = NULL;
node->_right = NULL;
return node;
}
// 通過前序遍歷的數組"ABD##E#H##CF##G##"構建二叉樹
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (a[*pi] == '#')
{
return NULL;
}
BTNode *node = (BTNode*)malloc(sizeof(BTNode));
node->_data = a[*pi];
++*pi;
node->_left = BinaryTreeCreate(a, n, pi);
++*pi;
node->_right = BinaryTreeCreate(a, n, pi);
return node;
}
// 二叉樹銷毀
void BinaryTreeDestory(BTNode** root)
{
if (*root != NULL)
{
if ((*root)->_left) // 有左孩子
BinaryTreeDestory(&(*root)->_left); // 銷毀左孩子子樹
if ((*root)->_right) // 有右孩子
BinaryTreeDestory(&(*root)->_right); // 銷毀右孩子子樹
free(*root); // 釋放根結點
*root = NULL; // 空指針賦NULL
}
}
// 二叉樹節點個數
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
// 二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->_left == NULL&&root->_right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
// 二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->_data == x)
{
return root;
}
BTNode* ret=BinaryTreeFind(root->_left,x);
if (ret != NULL)
{
return ret;
}
ret = BinaryTreeFind(root->_right, x);
if (ret != NULL)
{
return ret;
}
return NULL;
}
// 二叉樹前序遍歷
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
//printf("NULL ");
return;
}
printf("%c ", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
// 二叉樹中序遍歷
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
//printf("NULL ");
return;
}
BinaryTreeInOrder(root->_left);
printf("%c ", root->_data);
BinaryTreeInOrder(root->_right);
}
// 二叉樹後序遍歷
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
//printf("NULL ");
return;
}
BinaryTreePostOrder(root->_left);
BinaryTreePostOrder(root->_right);
printf("%c ", root->_data);
}
// 層序遍歷
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode *front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->_data);
if (front->_left)
{
QueuePush(&q, front->_left);
}
if (front->_right)
{
QueuePush(&q, front->_right);
}
}
}
// 判斷二叉樹是否是完全二叉樹
int BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode *front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
printf("%s ", front->_data);
if (front->_left)
{
QueuePush(&q, front->_left);
}
if (front->_right)
{
QueuePush(&q, front->_right);
}
}
while (!QueueEmpty(&q))
{
BTNode *front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
return 0;
}
}
return 1;
}
還有最後一個樹——線索二叉樹
它的出現還是為瞭簡約成本,實際上想一下算法和數據結構存在就是為瞭節約時間或空間,這個是節約不用的空指針域,
空的左孩子指針指向該結點的前驅,空的右孩子指針指向該結點的後繼。這種附加的指針值稱為線索,帶線索的二叉樹稱為線索二叉樹。
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#define MAXSIZE 100
typedef char ElemType;
typedef enum
{
Link,/*指向孩子結點*/Thread/*指向前驅或後繼*/
} PointerTag;
typedef struct Node
{
ElemType data;
struct Node *lchild;
struct Node *rchild;
PointerTag ltag,rtag;
}*BitThrTree,BitThrNode;
BitThrTree pre;
void CreateBitTree2(BitThrTree *T,char str[]);//創建搜索二叉樹
void InThreading(BitThrTree p);//中序線索化二叉樹
int InOrderThreading(BitThrTree *Thrt,BitThrTree T);//通過中序遍歷二叉樹T,使T中序線索化。Thrt是指向頭結點的指針
int InOrderTraverse(BitThrTree T,int (*visit)(BitThrTree e));//中序遍歷線索二叉樹
int Print(BitThrTree T);//打印二叉樹的結點和線索標志
BitThrNode* FindPoint(BitThrTree T,ElemType e);//在線索二叉樹中查找結點為e的指針
BitThrNode* InOrderPre(BitThrNode *p);//中序前驅
BitThrNode* InOrderPost(BitThrNode *p);//中序後繼
void DestroyBitTree(BitThrTree *T);//銷毀二叉樹
#include "LinkBiTree.h"
void CreateBitTree2(BitThrTree *T,char str[])//創建搜索二叉樹
{
char ch;
BitThrTree stack[MAXSIZE];
int top = -1;
int flag,k;
BitThrNode *p;
*T = NULL,k = 0;
ch = str[k];
while(ch != '\0')
{
switch(ch)
{
case '(':
stack[++top] = p;
flag = 1;
break;
case ')':
top--;
break;
case ',':
flag = 2;
break;
default:
p = (BitThrTree)malloc(sizeof(BitThrNode));
p->data = ch;
p->lchild = NULL;
p->rchild = NULL;
if(*T == NULL)
{
*T = p;
}
else
{
switch(flag)
{
case 1:
stack[top]->lchild = p;
break;
case 2:
stack[top]->rchild = p;
break;
}
if(stack[top]->lchild)
{
stack[top]->ltag = Link;
}
if(stack[top]->rchild)
{
stack[top]->rtag = Link;
}
}
}
ch = str[++k];
}
}
void InThreading(BitThrTree p)//中序線索化二叉樹
{
if(p)//左子樹線索化
{
InThreading(p->lchild);
if(!p->lchild)//前驅線索化
{
p->ltag = Thread;
p->lchild = pre;
}
if(!pre->rchild)//後繼線索化
{
pre->rtag = Thread;
pre->rchild = p;
}
pre = p;
InThreading(p->rchild);//右子樹線索化
}
}
int InOrderThreading(BitThrTree *Thrt,BitThrTree T)//通過中序遍歷二叉樹T,使T中序線索化。Thrt是指向頭結點的指針
{
if(!(*Thrt = (BitThrTree)malloc(sizeof(BitThrNode))))
{
exit(-1);//為頭結點分配單元
}
(*Thrt)->ltag = Link;//修改前驅線索標志
(*Thrt)->rtag = Thread;//修改後繼線索標志
(*Thrt)->rchild = *Thrt;//將頭結點的rchild指針指向自己
if(!T)//如果二叉樹為空,則將lchild指針指向自己
{
(*Thrt)->lchild = *Thrt;
}
else
{
(*Thrt)->lchild = T;//將頭結點的左指針指向根結點
pre = *Thrt;//將pre指向已經線索化的結點
InThreading(T);//中序遍歷進行中序線索化
/*將最後一個結點線索化*/
pre->rchild = *Thrt;//將最後一個結點的右指針指向頭結點
pre->rtag = Thread;//修改最後一個結點的rtag標志域
(*Thrt)->rchild = pre;//將頭結點的rchild指針指向最後一個結點
}
return 1;
}
int InOrderTraverse(BitThrTree T,int (*visit)(BitThrTree e))//中序遍歷線索二叉樹
{
BitThrTree p;
p = T->lchild ;//p指向根結點
while(p != T)//空樹或遍歷結束時,p == T
{
while(p->ltag == Link)
{
p = p->lchild ;
}
if(!visit(p))//打印
{
return 0;
}
while(p->rtag == Thread && p->rchild != T)//訪問後繼結點
{
p = p->rchild ;
visit(p);
}
p = p->rchild ;
}
return 1;
}
int Print(BitThrTree T)//打印二叉樹的結點和線索標志
{
static int k = 1;
printf("%2d\t%s\t %2c\t %s\t\n",k++,T->ltag == 0 ? "Link":"Thread",T->data ,T->rtag == 1 ? "Thread":"Link");
return 1;
}
BitThrNode* FindPoint(BitThrTree T,ElemType e)//在線索二叉樹中查找結點為e的指針
{
BitThrTree p;
p = T->lchild ;
while(p != T)
{
while(p->ltag == Link)
{
p = p->lchild ;
}
if(p->data == e)
{
return p;
}
while(p->rtag == Thread && p->rchild != T)
{
p = p->rchild ;
if(p->data == e)
{
return p;
}
}
p = p->rchild ;
}
return NULL;
}
BitThrNode* InOrderPre(BitThrNode *p)//中序前驅
{
if(p->ltag == Thread)//如果p的標志域ltag為線索,則p的左子樹結點為前驅
{
return p->lchild ;
}
else
{
pre = p->lchild ;//查找p的左孩子的最右下端結點
while(pre->rtag == Link)//右子樹非空時,沿右鏈往下查找
{
pre = pre->rchild ;
}
return pre;//pre就是最右下端結點
}
}
BitThrNode* InOrderPost(BitThrNode *p)//中序後繼
{
if(p->rtag == Thread)//如果p的標志域rtag為線索,則p的右子樹結點為後驅
{
return p->rchild ;
}
else
{
pre = p->rchild ;//查找p的右孩子的最左下端結點
while(pre->ltag == Link)//左子樹非空時,沿左鏈往下查找
{
pre = pre->lchild ;
}
return pre;//pre就是最左下端結點
}
}
void DestroyBitTree(BitThrTree *T)//銷毀二叉樹
{
if(*T)
{
if(!(*T)->lchild)
{
DestroyBitTree(&((*T)->lchild));
}
if(!(*T)->rchild)
{
DestroyBitTree(&((*T)->rchild));
}
free(*T);
*T = NULL;
}
}
#include "LinkBiTree.h"
int main(void)
{
BitThrTree T,Thrt;
BitThrNode *p,*pre,*post;
CreateBitTree2(&T,"(A(B(,D(G)),C(E(,H),F)))");
printf("線索二叉樹的輸出序列:\n");
InOrderThreading(&Thrt,T);
printf("序列 前驅標志 結點 後繼標志\n");
InOrderTraverse(Thrt,Print);
p = FindPoint(Thrt,'D');
pre = InOrderPre(p);
printf("元素D的中序直接前驅元素是:%c\n",pre->data);
post = InOrderPost(p);
printf("元素D的中序直接後驅元素是:%c\n",post->data);
p = FindPoint(Thrt,'E');
pre = InOrderPre(p);
printf("元素E的中序直接前驅元素是:%c\n",pre->data);
post = InOrderPost(p);
printf("元素E的中序直接後驅元素是:%c\n",post->data);
DestroyBitTree(&Thrt);
return 0;
}
哈夫曼樹
到這數據結構算過去一半瞭,我們先來總結一下

圖
終於樹結束瞭,累壞我瞭,開始圖
如果說樹是一對多的話,那麼圖就是多對多。
都見過地圖吧,像陜西就和山西連在瞭一起,還和內蒙古等等連,典型的多對多

如果說線性表和樹的專業術語比較繁瑣的話,那麼圖可能顛覆你的三觀,——還有這麼多的概念?介於圖的概念比較多,我們先來放概念,再講解
圖按照有無方向分為有向圖和無向圖。有向圖由頂點和弧構成,無向圖由頂點和邊檢成。弧有弧尾和弧頭之分。
圖按照邊或須的多少分為稀疏圖和稠密圖。如果任意兩個頂點之間都存在邊叫完全圖有向的叫有向完全圖。若無重復的邊或頂點到自身的邊則叫簡單圖。
圖中頂點之間有鄰接點、依附的概念。無向圖頂點的邊數叫做度,有向圖頂點分為入度和出度。
圖上的邊或弧上帶權則稱為網。
圖中頂點間存在路徑,兩頂點存在路徑則說明是連通的,如果路徑最終回到起始點則稱為環,當中不重復叫簡單路徑。若任意兩頂點都是連通的,則圖就是連通圖,有向則稱強連通圖。圖中有子圖,若子圖極大連通則就是連通分量,有向的則稱強連通分量。
無向圖中連通且n個頂點n-1條邊叫生成樹。有向圖中一頂點入度為0其餘頂點入度為1的叫有向樹。一個有向圖由若幹棵有向樹構成生成森林。
概念很多,一一刨析
頂點
像樹中的結點,聰明的彥祖一下就懂瞭,就是圖中的數據元素嘛,但是有不同之處,線性表中有空表,樹中有空樹,,但是可沒有空圖這一說法,why?舉個例子:像皇帝的新衣一樣,你總不能拿一張紙給別人說隻有聰明的人才能看到吧?還有就是在線性表中有線性關系,在樹中有層的關系,那麼在圖中呢?在圖中都有關系,一般來說我們將任意倆個頂點的關系用術語邊來表示,邊的集合可以為空
有向圖,無向圖
簡單的來看就是圖上沒有箭頭就為無向圖,反之有箭頭為有向圖。
如果非要我解釋的話,容我先引出無向邊和有向邊的概念
無向邊:反之就是這條邊無箭頭,如果是A——D,用(A,D)來表示
有向邊:簡單來說就是這條邊有箭頭,還是A->D,但是要用<A,D>來表示,註意:不能用<D,A>表示,其中,這條有向邊稱為弧,A是弧尾,D是弧頭也就是說箭頭指向的為弧頭
那麼有向圖和無向圖就簡單瞭,如果一個圖都由有向邊組成,則稱為有向圖,反之為無向圖
下面再引出倆個概念:完全有向圖,完全無向圖,
完全有向圖:
在有向圖中如果任意倆個頂點都存在方向相反的倆條弧,為完全有向圖
完全無向圖:
在無向圖中任意倆個頂點都存在邊相連,則稱為完全無向圖
還有倆個計算邊數的公式為:n*(n-1)/2 and n*(n-1),猜出來瞭吧,第一個是計算完全無向圖的,第二個是計算完全有向圖的
下面我們看倆個圖,自己判斷一下:


還有個稠密圖和稀疏圖,都是相對而言的,就像有錢一樣,如果我和乞丐比的話,我比較有錢,但是如果我和馬雲來比的話,可能都沒有辦法比較。
頂點和邊
下面我們把頂點和邊串起來講一下,他們之間也是有聯系的
對於無向圖來說,當倆個頂點通過一條邊相連時,稱為頂點相關聯,頂點度是和另一個頂點相關聯邊的條數,頂點可稱為互為鄰結點
對於有向圖來說,如果A->D稱為頂點A鄰接到頂點D,以A為頭的弧為入度,以D為尾的為出度
再來說路徑,路徑的長度為路徑的邊或弧的數目,其中第一個頂點和最後一個頂點相同的路徑稱為回路或環,序列中頂點不重復出現的路徑為簡單路徑,除瞭第一個頂點和最後一個頂點外,其餘頂點不重復出現的回路,又稱為簡單回路或簡單環
連通圖
圖中從一個頂點到達另一頂點,若存在至少一條路徑,則稱這兩個頂點是連通著的。例如圖 1 中,雖然 V1 和 V3 沒有直接關聯,但從 V1 到 V3 存在兩條路徑,分別是 V1-V2-V3 和 V1-V4-V3,因此稱 V1 和 V3 之間是連通的。

無向圖中,如果任意兩個頂點之間都能夠連通,則稱此無向圖為連通圖。例如,圖 2 中的無向圖就是一個連通圖,因為此圖中任意兩頂點之間都是連通的。若無向圖不是連通圖,但圖中存儲某個子圖符合連通圖的性質,則稱該子圖為連通分量。

強連通圖
有向圖中,若任意兩個頂點 Vi 和 Vj,滿足從 Vi 到 Vj 以及從 Vj 到 Vi 都連通,也就是都含有至少一條通路,則稱此有向圖為強連通圖。如圖 4 所示就是一個強連通圖。

與此同時,若有向圖本身不是強連通圖,但其包含的最大連通子圖具有強連通圖的性質,則稱該子圖為強連通分量。

剩下的就是圖有關的算法題瞭,用例題來說吧
- 圖的遍歷
給出N個點,M條邊的有向圖,對於每個點v,求A(v)表示從點v出發,能到達的編號最大的點。
按題目來每次考慮每個點可以到達點編號最大的點,不如考慮較大的點可以反向到達哪些點循環從N到1,則每個點i能訪問到的結點的A值都是i
每個點訪問一次,這個A值就是最優的,因為之後如果再訪問到這個結點那麼答案肯定沒當前大瞭
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
#define MAXL 100010
int N, M, A[MAXL];
vector<int> G[MAXL]; //vector存圖
void dfs(int x, int d) {
if(A[x]) return; //訪問過
A[x] = d;
for(int i=0; i<G[x].size(); i++)
dfs(G[x][i], d);
}
int main() {
int u, v;
scanf("%d%d", &N, &M);
for(int i=1; i<=M; i++) {
scanf("%d%d", &u, &v);
G[v].push_back(u); //反向建邊
}
for(int i=N; i; i--) dfs(i, i);
for(int i=1; i<=N; i++) printf("%d ", A[i]);
printf("\n");
return 0;
}
- 鄰接矩陣
給定一個整數矩陣

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
const int Len = 200 * 200 * 5 + 5,Inf = 1e9;
int dep[Len],cnt = 1,head[Len],s,t,S,T,cur[Len],val[Len],a[205][205],sumh[205],suml[205],LL,RR,n,m,sum,ans,minn;
struct node
{
int next,to,w;
}edge[Len << 1];
void add(int from,int to,int w)
{
edge[++ cnt].to = to;
edge[cnt].w = w;
edge[cnt].next = head[from];
head[from] = cnt;
}
int BFS()
{
queue<int> q;
memset(dep , 0 , sizeof dep);
q.push(S);dep[S] = 1;cur[S] = head[S];
while(!q.empty())
{
int p = q.front() ; q.pop();
for(int e = head[p] ; e ; e = edge[e].next)
{
int to = edge[e].to;
if(!dep[to] && edge[e].w)
{
dep[to] = dep[p] + 1;
cur[to] = head[to];
if(T == to) return dep[T];
q.push(to);
}
}
}
return dep[T];
}
int dfs(int u,int In)
{
if(u == T) return In;
int Out = 0;
for(int e = cur[u] ; e && In > 0 ; e = edge[e].next)
{
cur[u] = e;
int to = edge[e].to;
if(edge[e].w && dep[to] == dep[u] + 1)
{
int res = dfs(to , min(In , edge[e].w));
In -= res;
Out += res;
edge[e].w -= res;
edge[e ^ 1].w += res;
}
}
return (!Out) ? dep[u] = 0 : Out;
}
int Clone(int x,int y){return (x - 1) * n + y;}
bool check(int res)
{
memset(head , 0 , sizeof head) ; cnt = 1;
memset(val , 0 , sizeof val);
sum = ans = 0;
for(int i = 1 ; i < n ; i ++)//處理行
{
int now = Clone(i , m) , L = sumh[i] - res , R = sumh[i] + res;//L = sumh[i] - res , R = sumh[i] + res
add(s , now , R - L) , add(now , s , 0);
val[now] += L , val[s] -= L;
}
for(int i = 1 ; i < m ; i ++)
{
int now = Clone(n , i) , L = suml[i] - res , R = suml[i] + res;
add(now , s , R - L) , add(s , now , 0);
val[s] += L , val[now] -= L;
}
for(int i = 1 ; i < n ; i ++)
{
int now = Clone(i , m);
for(int j = 1 ; j < m ; j ++)
{
int to = Clone(i , j);
add(now , to , RR - LL) , add(to , now , 0);
val[to] += LL , val[now] -= LL;
}
}
for(int i = 1 ; i < m ; i ++)
{
int now = Clone(n , i);
for(int j = 1 ; j < n ; j ++)
{
int to = Clone(j , i);
add(to , now , RR - LL) , add(now , to , 0);
val[now] += LL , val[to] -= LL;
}
}
for(int i = 1 ; i <= n * m + 1 ; i ++)
{
if(val[i] > 0) add(S , i , val[i]) , add(i , S , 0) , sum += val[i];
if(val[i] < 0) add(i , T , -val[i]) , add(T , i , 0);
}
while(BFS()) ans += dfs(S , Inf);
if(ans == sum) return true;
return false;
}
signed main()
{
minn = 1e9;
scanf("%d %d",&n,&m);
n ++ , m ++;
s = n * m , t = n * m + 1 , S = n * m + 2 , T = n * m + 3;
for(int i = 1 ; i <= n - 1 ; i ++)
for(int j = 1 ; j <= m - 1 ; j ++)
{
scanf("%d",&a[i][j]);
sumh[i] += a[i][j] , suml[j] += a[i][j];
}
for(int i = 1 ; i <= n - 1 ; i ++) minn = min(minn , sumh[i]);
for(int i = 1 ; i <= m - 1 ; i ++) minn = min(minn , suml[i]);
scanf("%d %d",&LL,&RR);
int l = 0 , r = minn,anss;
while(l <= r)
{
int mid = (l + r) >> 1;
if(check(mid)) anss = mid , r = mid - 1;
else l = mid + 1;
}
printf("%d\n",anss);
return 0;
}
來自:矩陣
再來一個深搜結束吧
- 深度優先遍歷
給出N個點,M條邊的有向圖,對於每個點v,求A(v)表示從點v出發,能到達的編號最大的點
比較簡單:反向建邊 + dfs
按題目來每次考慮每個點可以到達點編號最大的點,不如考慮較大的點可以反向到達哪些點循環從N到1,則每個點i能訪問到的結點的A值都是i每個點訪問一次,這個A值就是最優的,因為之後如果再訪問到這個結點那麼答案肯定沒當前大瞭
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
#define MAXL 100010
int N, M, A[MAXL];
vector<int> G[MAXL]; //vector存圖
void dfs(int x, int d) {
if(A[x]) return; //訪問過
A[x] = d;
for(int i=0; i<G[x].size(); i++)
dfs(G[x][i], d);
}
int main() {
int u, v;
scanf("%d%d", &N, &M);
for(int i=1; i<=M; i++) {
scanf("%d%d", &u, &v);
G[v].push_back(u); //反向建邊
}
for(int i=N; i; i--) dfs(i, i);
for(int i=1; i<=N; i++) printf("%d ", A[i]);
printf("\n");
return 0;
}
深搜有瞭,不上廣搜有點過意不去,算瞭再來個廣搜
- 廣搜
有一個 n×m 的棋盤,在某個點 (x,y) 上有一個馬,要求你計算出馬到達棋盤上任意一個點最少要走幾步。
#include<iostream>//P1443
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>//運用瞭隊列
#include<cmath>
using namespace std;
const int dx[8]={-1,-2,-2,-1,1,2,2,1};
const int dy[8]={2,1,-1,-2,2,1,-1,-2};//8個方向
queue<pair<int,int> > q;
int f[500][500];//存步數
bool vis[500][500];//走沒走過
int main()
{
int n,m,x,y;
memset(f,-1,sizeof(f));memset(vis,false,sizeof(vis));
cin>>n>>m>>x>>y;
f[x][y]=0;vis[x][y]=true;q.push(make_pair(x,y));
while(!q.empty())
{
int xx=q.front().first,yy=q.front().second;q.pop();//取隊首並出隊
for(int i=0;i<8;i++)
{
int u=xx+dx[i],v=yy+dy[i];
if(u<1||u>n||v<1||v>m||vis[u][v])continue;//出界或走過就不走
vis[u][v]=true;q.push(make_pair(u,v));f[u][v]=f[xx][yy]+1;
}
}
for(int i=1;i<=n;i++)
{for(int j=1;j<=m;j++)printf("%-5d",f[i][j]);printf("\n");}//註意場寬!!
return 0;
}
- 最短路徑
實際上對於最短路徑,讓我看的話,它和深搜,廣搜差不多
主要是這倆個大佬發明的東西
- 迪傑斯特拉算法
- 弗洛伊德算法
下面就按順序來看一下
Dijkstra算法采用的是一種貪心的策略,聲明一個數組dis來保存源點到各個頂點的最短距離和一個保存已經找到瞭最短路徑的頂點的集合:T,初始時,原點 s 的路徑權重被賦為 0 (dis[s] = 0)。若對於頂點 s 存在能直接到達的邊(s,m),則把dis[m]設為w(s, m),同時把所有其他(s不能直接到達的)頂點的路徑長度設為無窮大。初始時,集合T隻有頂點s。然後,從dis數組選擇最小值,則該值就是源點s到該值對應的頂點的最短路徑,並且把該點加入到T中,OK,此時完成一個頂點,然後,我們需要看看新加入的頂點是否可以到達其他頂點並且看看通過該頂點到達其他點的路徑長度是否比源點直接到達短,如果是,那麼就替換這些頂點在dis中的值。最後,又從dis中找出最小值,重復上述動作,直到T中包含瞭圖的所有頂點。
這個總體上是一個:廣度優先搜索解決賦權有向圖或者無向圖的單源最短路徑問題,算法最終得到一個最短路徑樹
#pragma once
#include<iostream>
#include<string>
using namespace std;
//鄰接矩陣保存
//記錄起點到每個頂點的最短路徑的信息
struct Dis {
string path;
int value;
bool visit;
Dis() {
visit = false;
value = 0;
path = "";
}
};
class Graph_DG {
private:
int vexnum; //圖的頂點個數
int edge; //圖的邊數
int **arc; //鄰接矩陣
Dis * dis; //記錄各個頂點最短路徑的信息
public:
//構造函數
Graph_DG(int vexnum, int edge);
//析構函數
~Graph_DG();
// 判斷我們每次輸入的的邊的信息是否合法
//頂點從1開始編號
bool check_edge_value(int start, int end, int weight);
//創建圖
void createGraph();
//打印鄰接矩陣
void print();
//求最短路徑
void Dijkstra(int begin);
//打印最短路徑
void print_path(int);
};
#include"Dijkstra.h"
//構造函數
Graph_DG::Graph_DG(int vexnum, int edge) {
//初始化頂點數和邊數
this->vexnum = vexnum;
this->edge = edge;
//為鄰接矩陣開辟空間和賦初值
arc = new int*[this->vexnum];
dis = new Dis[this->vexnum];
for (int i = 0; i < this->vexnum; i++) {
arc[i] = new int[this->vexnum];
for (int k = 0; k < this->vexnum; k++) {
//鄰接矩陣初始化為無窮大
arc[i][k] = INT_MAX;
}
}
}
//析構函數
Graph_DG::~Graph_DG() {
delete[] dis;
for (int i = 0; i < this->vexnum; i++) {
delete this->arc[i];
}
delete arc;
}
// 判斷我們每次輸入的的邊的信息是否合法
//頂點從1開始編號
bool Graph_DG::check_edge_value(int start, int end, int weight) {
if (start<1 || end<1 || start>vexnum || end>vexnum || weight < 0) {
return false;
}
return true;
}
void Graph_DG::createGraph() {
cout << "請輸入每條邊的起點和終點(頂點編號從1開始)以及其權重" << endl;
int start;
int end;
int weight;
int count = 0;
while (count != this->edge) {
cin >> start >> end >> weight;
//首先判斷邊的信息是否合法
while (!this->check_edge_value(start, end, weight)) {
cout << "輸入的邊的信息不合法,請重新輸入" << endl;
cin >> start >> end >> weight;
}
//對鄰接矩陣對應上的點賦值
arc[start - 1][end - 1] = weight;
//無向圖添加上這行代碼
//arc[end - 1][start - 1] = weight;
++count;
}
}
void Graph_DG::print() {
cout << "圖的鄰接矩陣為:" << endl;
int count_row = 0; //打印行的標簽
int count_col = 0; //打印列的標簽
//開始打印
while (count_row != this->vexnum) {
count_col = 0;
while (count_col != this->vexnum) {
if (arc[count_row][count_col] == INT_MAX)
cout << "∞" << " ";
else
cout << arc[count_row][count_col] << " ";
++count_col;
}
cout << endl;
++count_row;
}
}
void Graph_DG::Dijkstra(int begin){
//首先初始化我們的dis數組
int i;
for (i = 0; i < this->vexnum; i++) {
//設置當前的路徑
dis[i].path = "v" + to_string(begin) + "-->v" + to_string(i + 1);
dis[i].value = arc[begin - 1][i];
}
//設置起點的到起點的路徑為0
dis[begin - 1].value = 0;
dis[begin - 1].visit = true;
int count = 1;
//計算剩餘的頂點的最短路徑(剩餘this->vexnum-1個頂點)
while (count != this->vexnum) {
//temp用於保存當前dis數組中最小的那個下標
//min記錄的當前的最小值
int temp=0;
int min = INT_MAX;
for (i = 0; i < this->vexnum; i++) {
if (!dis[i].visit && dis[i].value<min) {
min = dis[i].value;
temp = i;
}
}
//cout << temp + 1 << " "<<min << endl;
//把temp對應的頂點加入到已經找到的最短路徑的集合中
dis[temp].visit = true;
++count;
for (i = 0; i < this->vexnum; i++) {
//註意這裡的條件arc[temp][i]!=INT_MAX必須加,不然會出現溢出,從而造成程序異常
if (!dis[i].visit && arc[temp][i]!=INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) {
//如果新得到的邊可以影響其他為訪問的頂點,那就就更新它的最短路徑和長度
dis[i].value = dis[temp].value + arc[temp][i];
dis[i].path = dis[temp].path + "-->v" + to_string(i + 1);
}
}
}
}
void Graph_DG::print_path(int begin) {
string str;
str = "v" + to_string(begin);
cout << "以"<<str<<"為起點的圖的最短路徑為:" << endl;
for (int i = 0; i != this->vexnum; i++) {
if(dis[i].value!=INT_MAX)
cout << dis[i].path << "=" << dis[i].value << endl;
else {
cout << dis[i].path << "是無最短路徑的" << endl;
}
}
}
#include"Dijkstra.h"
//檢驗輸入邊數和頂點數的值是否有效,可以自己推算為啥:
//頂點數和邊數的關系是:((Vexnum*(Vexnum - 1)) / 2) < edge
bool check(int Vexnum, int edge) {
if (Vexnum <= 0 || edge <= 0 || ((Vexnum*(Vexnum - 1)) / 2) < edge)
return false;
return true;
}
int main() {
int vexnum; int edge;
cout << "輸入圖的頂點個數和邊的條數:" << endl;
cin >> vexnum >> edge;
while (!check(vexnum, edge)) {
cout << "輸入的數值不合法,請重新輸入" << endl;
cin >> vexnum >> edge;
}
Graph_DG graph(vexnum, edge);
graph.createGraph();
graph.print();
graph.Dijkstra(1);
graph.print_path(1);
system("pause");
return 0;
}
弗洛伊德算法,我就使用偽代碼來寫瞭,
//總體上是一個二重循環加上一個三重循環,主要運用於所有頂點到所有頂點的最短路徑問題
void ShortestPath FLOYD(MGraph G, PathMatrix &p[], DistanceMatrix &D){
//用Floyd算法求有向網中各對頂點v和w之間的最短路徑P[v][w]及其帶權長
//度D[v][w].若P[v][w][u]為TRUE,則u是從v到w當前求得最短路徑上的頂點。
for(v = 0; v < G.vexnum; ++v) //各對結點之間初始已知路徑及距離
for(w = 0; w < G.vexnum; ++w){
D[v][w] = G.arcs[v][w];
for(u = 0; u < G.vexnum; ++w) P[v][w][u] = FALSE;
if(D[v][w] < INFINITY){ //從v到w有直接路徑
P[v][w][v] = TRUE; P[v][w][w] = TRUE;
}//if
}//for
for(u = 0; u < G.vexnum; ++u)
for(v = 0; v<G.vexnum; ++v)
for(w = 0; w<G.vexnum; ++w)
if(D[v][u] + D[u][w] < D[v][w]){ //從v經u到w的一條路徑更短
D[v][w] = D[v][u] + D[u][w];
for(i = 0; i<G.vexnum; ++i)
P[v][w][i] = P[v][u][i] || P[u][w][i];
}//if
}//ShortestPath.FLOYD
圖用網上十分流行的一句話來結尾,
世界上最遙遠的距離是我找不到與你的最短路徑 , 哭瞭
附:如果你還在糾結到底哪門語言作為主語言的話不妨來看看(入門時刻)
一、為什麼要學主流語言?
1.古老
實際上由於我的年紀也比較小,所以在選擇語言時肯定會選擇大方向的語言,不能像前幾年的VB一樣,像我小學時候的語言,如果現在學他的話,那麼你真的要吃土瞭
2.超前
上面的VB是比較古老的語言瞭,還有一種就是比較超前的語言,像近幾年的號稱取代c++的高性能語言,go,rust,但是我不太認可,因為大廠的架構不可能直接更換語言,小廠又會選擇主流語言,以便於獲取更廉價的勞動力,所以說我也不建議用超前的語言來進行入門
3.過於簡單的
這時就要請出我們的python ,php,這類語言一般很簡單的可以入門,也可以快速的開發出一個比較實用的應用,所以受到廣大初學者和科研人員的追捧,但是由於入門簡單加上深入困難,所以可替代性高,可能這時有的同學就要說瞭那我簡單入門後再轉其他的語言不好嗎? 兄弟,簡單語言學過瞭以後你還會想難的嗎?
總結
上面主要說瞭3點,當然還有,但是我就不在囉嗦瞭,所以說大傢如果初學編程的話最好學你目前看來,2-4年行情還是不錯的語言
我大致想到以下幾個
- java
- c/c++
建議這倆個中挑一個主要學習,深度學習
java
優點:由於Java面向移動端兼容的性能真的太好瞭,這也就造就瞭,java崗位的井噴式的增長
平臺: 軟件/應用程序,Web和移動開發。
難度:和c++差不多,但是沒有c++難,因為Java也是c++開發出來的,其中移除瞭c++指針,總體還是難
工資:平均工資高於大部分的語言
c
是上一輩人使用的編程語言瞭,所以說它在單片機——集成電路芯片,使用還是比較廣泛的,和c++一樣它也具有高性能的優點,但是我們這一輩人我建議直接開c++,
c++
今天仍然在使用原始的C語言,但是大多數現代開發人員已改用C ++。
計算機程序,移動應用程序,視頻遊戲,操作系統,整個瀏覽器,甚至在一定程度上還可以進行Web開發-如果您能想到的東西,C ++就能做到。且它運行快速。
平臺 主要是軟件開發;可以在各種情況下使用。
學習難度: 比較難學,特別是對於初學者。
平均工資 :好像c++平均工資比Java高已經是不爭的事實瞭,畢竟物以稀為貴莫。
優點: 純粹的多功能性。您可以將其用於任何事情。可以很好地翻譯成其他語言。快速而強大。
缺點: 對於初學者來說,不是正確的第一語言。由於年代久遠,因此在應用程序中具有普遍性,也異常復雜。對於Web開發而言並不理想。
後續
如果你第一語言已經掌握的差不多瞭,在大二下,那麼此時可以根據時勢來考慮第二語言,下面我隻提出我自己的薄見
- 還是上面的如果你學瞭Java,或c++那就繼續或者學習他們的拓展,QT,數據庫,底層框架,Web基礎等等
- 或者你就緊跟時代潮流,什麼火,去學什麼,前幾天的鴻蒙,就可以學的搭建,還要rust語言,go語言等等,前提是你能保證第一語言,餓不死你,不然就繼續紮根第一語言
最後
到此這篇關於C++數據結構的文章就介紹到這瞭,更多相關C++數據結構內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!