Python機器學習多層感知機原理解析
隱藏層
我們在前面描述瞭仿射變換,它是一個帶有偏置項的線性變換。首先,回想下之前下圖中所示的softmax回歸的模型結構。該模型通過單個仿射變換將我們的輸入直接映射到輸出,然後進行softmax操作。如果我們的標簽通過仿射變換後確實與我們的輸入數據相關,那麼這種方法就足夠瞭。但是,仿射變換中的線性是一個很強的假設。
我們的數據可能會有一種表示,這種表示會考慮到我們的特征之間的相關交互作用。在此表示的基礎上建立一個線性模型可能會是合適的,但我們不知道如何手動計算這麼一種表示。對於深度神經網絡,我們使用觀測數據來聯合學習隱藏層表示和應用於該表示的線性預測器。
我們可以通過在網絡中加入一個或多個隱藏層來克服線性模型的限制,使其能處理更普遍的函數關系類型。要做到這一點,最簡單的方法是將許多全連接層堆疊在一起。每一層都輸出到上面的層,直到生成最後的輸出。我們可以把前L−1層看作表示,把最後一層看作線性預測器。這種架構通常稱為多層感知機(multilayer perceptron),通常縮寫為MLP。下面,我們以圖的方式描述瞭多層感知機。
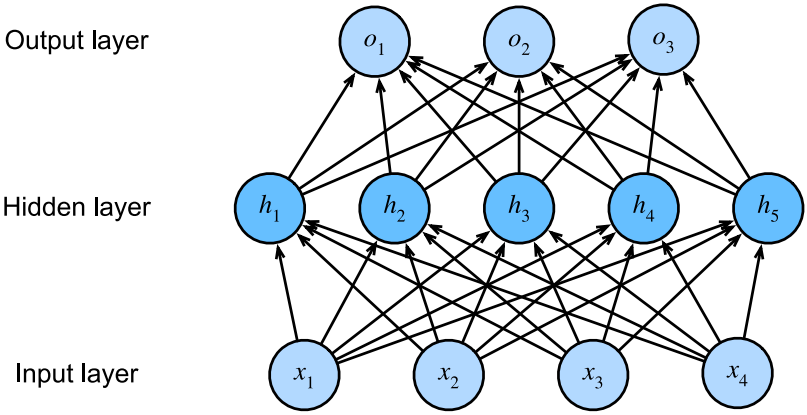
這個多層感知機有4個輸入,3個輸出,其隱藏層包含5個隱藏單元。輸入層不涉及任何計算,因此使用此網絡產生輸出隻需要實現隱藏層和輸出層的計算;因此,這個多層感知機的層數為2。註意,這個層都是全連接的。每個輸入都會影響隱藏層中的每個神經元,而隱藏層中的每個神經元又會影響輸出層的每個神經元。
然而,具有全連接層的多層感知機的參數開銷可能會高得令人望而卻步,即使在不改變輸入和輸出大小的情況下,也可能促使在參數節約和模型有效性之間進行權衡。
從線性到非線性

註意,在添加隱藏層之後,模型現在需要跟蹤和更新額外的參數。
可我們能從中得到什麼好處呢?這裡我們會驚訝地發現:在上面定義的模型裡,我們沒有好處。上面的隱藏單元由輸入的仿射函數給出,而輸出(softmax操作前)隻是隱藏單元的仿射函數。仿射函數的仿射函數本身就是仿射函數。但是我們之前的線性模型已經能夠表示任何仿射函數。

由於 X中的每一行對應於小批量中的一個樣本,處於記號習慣的考量,我們定義非線性函數 σ也以按行的方式作用於其輸入,即一次計算一個樣本。我們在之前以相同的方式使用瞭softmax符號來表示按行操作。但是在本節中,我們應用於隱藏層的激活函數通常不僅僅是按行的,而且也是按元素。這意味著在計算每一層的線性部分之後,我們可以計算每個激活值,而不需要查看其他隱藏單元所取的值。對於大多數激活函數都是這樣。
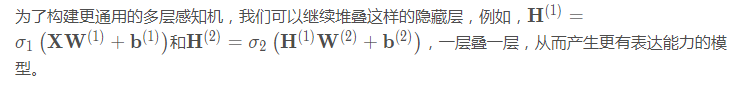
激活函數
激活函數通過計算加權和並加上偏置來確定神經元是否應該被激活。它們是輸入信號轉換為輸出的可微運算。大多數激活函數都是非線性的。由於激活函數是深度學習的基礎,下面簡要介紹一些常見的激活函數。
import torch from d2l import torch as d2l
ReLU函數
最受歡迎的選擇是線性整流單元,因為它實現簡單,同時在各種預測任務中表現良好。ReLU提供瞭一種非常簡單的非線性變換。給定元素x ,ReLU函數被定義為該元素與0的最大值:
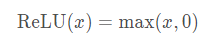
通俗地說,ReLU函數通過將相應的激活值設為0來僅保留正元素並丟棄所有負元素。為瞭直觀感受下,我們可以畫出函數的曲線圖。下圖所示,激活函數是分段線性的。
x = torch.arange(-8, 8, 0.1, requires_grad=True) y = torch.relu(x) d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))
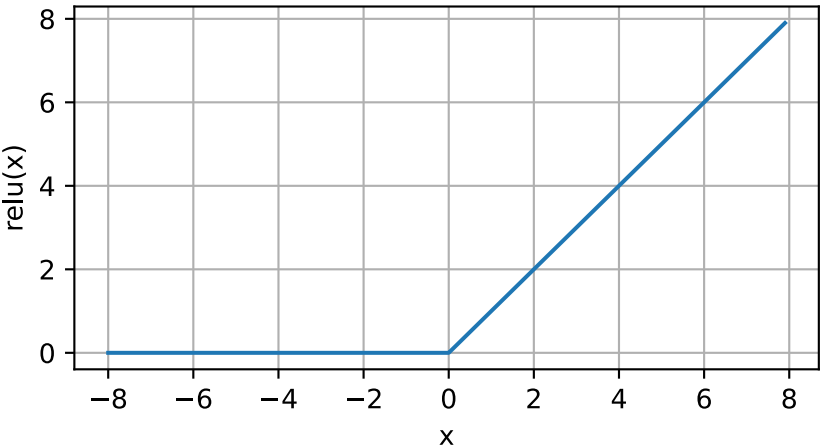
註意,當輸入值精確等於0時,ReLU函數不可導。在此時,我們默認使用左側的導數,即當輸入為0時導數為0。我們可以忽略這種情況,因為輸入可能永遠都不會是0。這裡用上一句古老的諺語,“如果微妙的邊界條件很重要,我們很可能是在研究數學而非工程”,這個觀點正好適用於這裡。下面我們繪制ReLU函數的導數。
y.backward(torch.ones_ilke(x), retain_graph=True) d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))
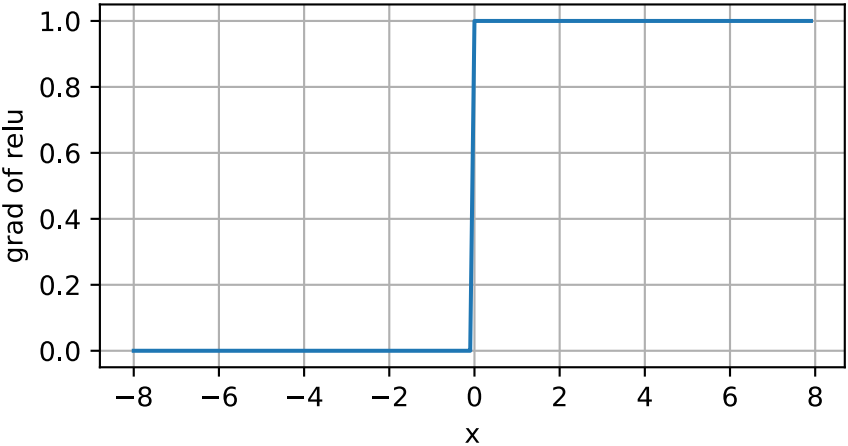
使用ReLU的原因是,它求導表現得特別好,要麼讓參數消失,要麼讓參數通過。這使得優化表現得更好,並且ReLU減輕瞭困擾以往神經網絡梯度消失問題。
註意,ReLU函數有許多變體,包括參數化ReLU函數(Parameterized ReLU)。該變體為ReLU添加瞭一個線性項,因此即使參數是負的,某些信息仍然可以通過:
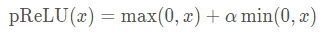
sigmoid函數

在最早的神經網絡中,科學傢們感興趣的是對“激發”或“不激發”的生物神經元進行建模。因此,這一領域的先驅,如人工神經元的發明者麥卡洛克和皮茨,從他們開始就專註於閾值單元。閾值單元在其輸入低於某個閾值時取值為0,當輸入超過閾值時取1。
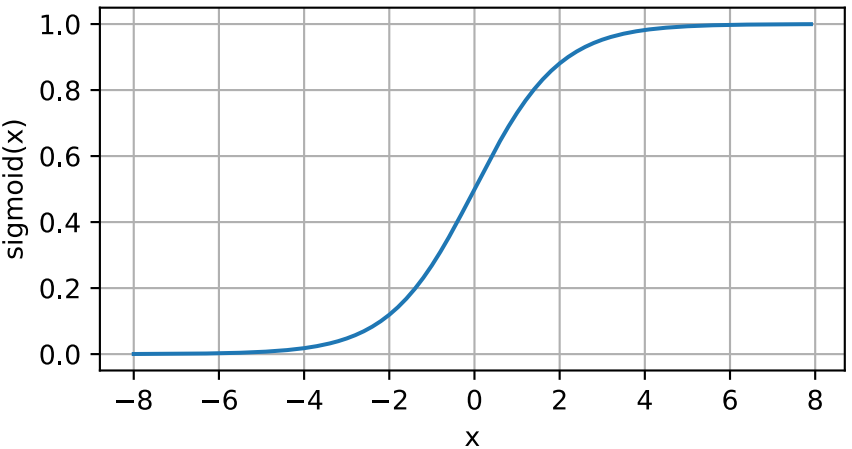
當人們的註意力逐漸轉移到梯度的學習時,sigmoid函數是一個自然的選擇,因為它是一個平滑的、可微的閾值單元近似。當我們想要將輸出視作二分類問題的概率時,sigmoid仍然被廣泛用作輸出單元上的激活函數(可以將sigmoid視為softmax的特例)。然而, sigmoid在隱藏層中已經較少使用,它在大部分時候已經被更簡單、更容易訓練的ReLU所取代。
tanh函數
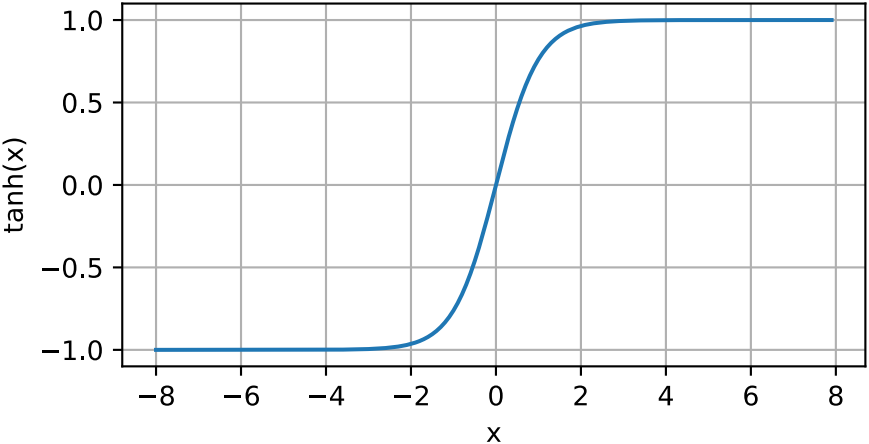
與sigmoid函數類似,tanh(雙曲正切)函數也能將其輸入壓縮轉換到區間(-1,1)上。tanh函數的公式如下:
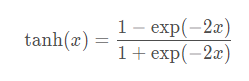
下面我們繪制tanh函數。註意,當輸入在0附近時,tanh函數接近線性變換。函數的形狀類似於sigmoid函數,不同的是tanh函數關於坐標系原點中心對稱。
以上就是Python機器學習多層感知機原理解析的詳細內容,更多關於Python機器學習多層感知機的資料請關註WalkonNet其它相關文章!
推薦閱讀:
- 人工智能學習Pytorch梯度下降優化示例詳解
- Pytorch中的backward()多個loss函數用法
- pytorch繪制曲線的方法
- pytorch_detach 切斷網絡反傳方式
- PyTorch 如何自動計算梯度