Python機器學習應用之基於BP神經網絡的預測篇詳解
一、Introduction
1 BP神經網絡的優點
- 非線性映射能力:BP神經網絡實質上實現瞭一個從輸入到輸出的映射功能,數學理論證明三層的神經網絡就能夠以任意精度逼近任何非線性連續函數。這使得其特別適合於求解內部機制復雜的問題,即BP神經網絡具有較強的非線性映射能力。
- 自學習和自適應能力:BP神經網絡在訓練時,能夠通過學習自動提取輸入、輸出數據間的“合理規則”,並自適應地將學習內容記憶於網絡的權值中。即BP神經網絡具有高度自學習和自適應的能力。
- 泛化能力:所謂泛化能力是指在設計模式分類器時,即要考慮網絡在保證對所需分類對象進行正確分類,還要關心網絡在經過訓練後,能否對未見過的模式或有噪聲污染的模式,進行正確的分類。也即BP神經網絡具有將學習成果應用於新知識的能力。
2 BP神經網絡的缺點
- 局部極小化問題:從數學角度看,傳統的 BP神經網絡為一種局部搜索的優化方法,它要解決的是一個復雜非線性化問題,網絡的權值是通過沿局部改善的方向逐漸進行調整的,這樣會使算法陷入局部極值,權值收斂到局部極小點,從而導致網絡訓練失敗。加上BP神經網絡對初始網絡權重非常敏感,以不同的權重初始化網絡,其往往會收斂於不同的局部極小,這也是每次訓練得到不同結果的根本原因
- BP 神經網絡算法的收斂速度慢:由於BP神經網絡算法本質上為梯度下降法,它所要優化的目標函數是非常復雜的,因此,必然會出現“鋸齒形現象”,這使得BP算法低效;又由於優化的目標函數很復雜,它必然會在神經元輸出接近0或1的情況下,出現一些平坦區,在這些區域內,權值誤差改變很小,使訓練過程幾乎停頓;BP神經網絡模型中,為瞭使網絡執行BP算法,不能使用傳統的一維搜索法求每次迭代的步長,而必須把步長的更新規則預先賦予網絡,這種方法也會引起算法低效。以上種種,導致瞭BP神經網絡算法收斂速度慢的現象。
- BP 神經網絡結構選擇不一:BP神經網絡結構的選擇至今尚無一種統一而完整的理論指導,一般隻能由經驗選定。網絡結構選擇過大,訓練中效率不高,可能出現過擬合現象,造成網絡性能低,容錯性下降,若選擇過小,則又會造成網絡可能不收斂。而網絡的結構直接影響網絡的逼近能力及推廣性質。因此,應用中如何選擇合適的網絡結構是一個重要的問題。
二、實現過程
1 Demo
#%% 基礎數組運算庫導入
import numpy as np
# 畫圖庫導入
import matplotlib.pyplot as plt
# 導入三維顯示工具
from mpl_toolkits.mplot3d import Axes3D
# 導入BP模型
from sklearn.neural_network import MLPClassifier
# 導入demo數據制作方法
from sklearn.datasets import make_classification
from sklearn.metrics import classification_report, confusion_matrix
import seaborn as sns
import warnings
from sklearn.exceptions import ConvergenceWarning
#%%模型訓練
# 制作五個類別的數據,每個類別1000個樣本
train_samples, train_labels = make_classification(n_samples=1000, n_features=3,
n_redundant=0,n_classes=5, n_informative=3,
n_clusters_per_class=1,class_sep=3, random_state=10)
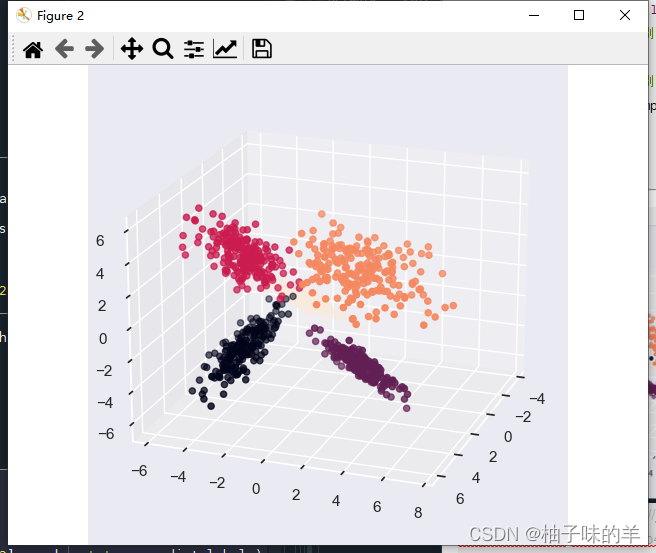
# 將五個類別的數據進行三維顯示
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=20, azim=20)
ax.scatter(train_samples[:, 0], train_samples[:, 1], train_samples[:, 2], marker='o', c=train_labels)
plt.title('Demo Data Map')

#%% 建立 BP 模型, 采用sgd優化器,relu非線性映射函數
BP = MLPClassifier(solver='sgd',activation = 'relu',max_iter = 500,alpha = 1e-3,
hidden_layer_sizes = (32,32),random_state = 1)
# 進行模型訓練
with warnings.catch_warnings():
warnings.filterwarnings("ignore", category=ConvergenceWarning,
module="sklearn")
BP.fit(train_samples, train_labels)
# 查看 BP 模型的參數
print(BP)
#%% 進行模型預測
predict_labels = BP.predict(train_samples)
# 顯示預測的散點圖
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=20, azim=20)
ax.scatter(train_samples[:, 0], train_samples[:, 1], train_samples[:, 2], marker='o', c=predict_labels)
plt.title('Demo Data Predict Map with BP Model')
# 顯示預測分數
print("預測準確率: {:.4f}".format(BP.score(train_samples, train_labels)))
# 可視化預測數據
print("真實類別:", train_labels[:10])
print("預測類別:", predict_labels[:10])
# 準確率等報表
print(classification_report(train_labels, predict_labels))
# 計算混淆矩陣
classes = [0, 1, 2, 3]
cofusion_mat = confusion_matrix(train_labels, predict_labels, classes)
sns.set()
figur, ax = plt.subplots()
# 畫熱力圖
sns.heatmap(cofusion_mat, cmap="YlGnBu_r", annot=True, ax=ax)
ax.set_title('confusion matrix') # 標題
ax.set_xticklabels([''] + classes, minor=True)
ax.set_yticklabels([''] + classes, minor=True)
ax.set_xlabel('predict') # x軸
ax.set_ylabel('true') # y軸
plt.show()


#%%# 進行新的測試數據測試
test_sample = np.array([[-1, 0.1, 0.1]])
print(f"{test_sample} 類別是: ", BP.predict(test_sample))
print(f"{test_sample} 類別概率分別是: ", BP.predict_proba(test_sample))
test_sample = np.array([[-1.2, 10, -91]])
print(f"{test_sample} 類別是: ", BP.predict(test_sample))
print(f"{test_sample} 類別概率分別是: ", BP.predict_proba(test_sample))
test_sample = np.array([[-12, -0.1, -0.1]])
print(f"{test_sample} 類別是: ", BP.predict(test_sample))
print(f"{test_sample} 類別概率分別是: ", BP.predict_proba(test_sample))
test_sample = np.array([[100, -90.1, -9.1]])
print(f"{test_sample} 類別是: ", BP.predict(test_sample))
print(f"{test_sample} 類別概率分別是: ", BP.predict_proba(test_sample))

2 基於BP神經網絡的乳腺癌分類預測
#%%基於BP神經網絡的乳腺癌分類
#基本庫導入
# 導入乳腺癌數據集
from sklearn.datasets import load_breast_cancer
# 導入BP模型
from sklearn.neural_network import MLPClassifier
# 導入訓練集分割方法
from sklearn.model_selection import train_test_split
# 導入預測指標計算函數和混淆矩陣計算函數
from sklearn.metrics import classification_report, confusion_matrix
# 導入繪圖包
import seaborn as sns
import matplotlib.pyplot as plt
# 導入三維顯示工具
from mpl_toolkits.mplot3d import Axes3D
# 導入乳腺癌數據集
cancer = load_breast_cancer()
# 查看數據集信息
print('breast_cancer數據集的長度為:',len(cancer))
print('breast_cancer數據集的類型為:',type(cancer))
# 分割數據為訓練集和測試集
cancer_data = cancer['data']
print('cancer_data數據維度為:',cancer_data.shape)
cancer_target = cancer['target']
print('cancer_target標簽維度為:',cancer_target.shape)
cancer_names = cancer['feature_names']
cancer_desc = cancer['DESCR']
#分為訓練集與測試集
cancer_data_train,cancer_data_test = train_test_split(cancer_data,test_size=0.2,random_state=42)#訓練集
cancer_target_train,cancer_target_test = train_test_split(cancer_target,test_size=0.2,random_state=42)#測試集

#%%# 建立 BP 模型, 采用Adam優化器,relu非線性映射函數
BP = MLPClassifier(solver='adam',activation = 'relu',max_iter = 1000,alpha = 1e-3,hidden_layer_sizes = (64,32, 32),random_state = 1)
# 進行模型訓練
BP.fit(cancer_data_train, cancer_target_train)
#%% 進行模型預測
predict_train_labels = BP.predict(cancer_data_train)
# 可視化真實數據
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=20, azim=20)
ax.scatter(cancer_data_train[:, 0], cancer_data_train[:, 1], cancer_data_train[:, 2], marker='o', c=cancer_target_train)
plt.title('True Label Map')
plt.show()
# 可視化預測數據
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=20, azim=20)
ax.scatter(cancer_data_train[:, 0], cancer_data_train[:, 1], cancer_data_train[:, 2], marker='o', c=predict_train_labels)
plt.title('Cancer with BP Model')
plt.show()

#%% 顯示預測分數
print("預測準確率: {:.4f}".format(BP.score(cancer_data_test, cancer_target_test)))
# 進行測試集數據的類別預測
predict_test_labels = BP.predict(cancer_data_test)
print("測試集的真實標簽:\n", cancer_target_test)
print("測試集的預測標簽:\n", predict_test_labels)
#%% 進行預測結果指標統計 統計每一類別的預測準確率、召回率、F1分數
print(classification_report(cancer_target_test, predict_test_labels))

#%% 計算混淆矩陣
confusion_mat = confusion_matrix(cancer_target_test, predict_test_labels)
# 打印混淆矩陣
print(confusion_mat)
# 將混淆矩陣以熱力圖的方式顯示
sns.set()
figure, ax = plt.subplots()
# 畫熱力圖
sns.heatmap(confusion_mat, cmap="YlGnBu_r", annot=True, ax=ax)
# 標題
ax.set_title('confusion matrix')
# x軸為預測類別
ax.set_xlabel('predict')
# y軸實際類別
ax.set_ylabel('true')
plt.show()

註:之前還做過基於BP神經網絡的人口普查數據預測,有需要的猿友私信
三、Keys
BP神經網絡的要點在於前向傳播和誤差反向傳播,來對參數進行更新,使得損失最小化。
它是一個迭代算法,基本思想是:
- 先計算每一層的狀態和激活值,直到最後一層(即信號是前向傳播的);
- 計算每一層的誤差,誤差的計算過程是從最後一層向前推進的(反向傳播);
- 更新參數(目標是誤差變小)。迭代前面兩個步驟,直到滿足停止準則(比如相鄰兩次迭代的誤差的差別很小)。
886~~~
到此這篇關於Python機器學習應用之基於BP神經網絡的預測篇詳解的文章就介紹到這瞭,更多相關Python BP神經網絡內容請搜索WalkonNet以前的文章或繼續瀏覽下面的相關文章希望大傢以後多多支持WalkonNet!
推薦閱讀:
- Python機器學習應用之決策樹分類實例詳解
- Python機器學習應用之基於天氣數據集的XGBoost分類篇解讀
- Python機器學習應用之基於LightGBM的分類預測篇解讀
- 使用Python和scikit-learn創建混淆矩陣的示例詳解
- Python機器學習之決策樹和隨機森林